大学生体质健康综合评价
2014-10-24温勤勤朱家明
温勤勤,朱家明,韩 谊,张 丽
(安徽财经大学 统计与应用数学学院,安徽 蚌埠 233030)
近年来随着人们生活水平的提高,健康问题也引起人们更多的关注。大学生作为社会主义建设的后备力量,其体质健康更应予以高度重视。目前,在美国比较普遍使用的健康体质测试方法,主要由有氧运动研究所1987年建立的FITNESSGRAM,选用的指标都是人体健康有关的[1]。日本对体制研究也十分重视,日本的体质研究主要从机能评定、形态发育与精神状态三个方面进行[2]。体质健康综合评价,国内早在20世纪80年代就开始研究,近20年国内报告中提及指数法、离差法、百分位法等。近年,有体育、教育和卫生界的学者采用聚类分析、判别分析和主成分分析等统计数学方法,进行体制综合评价,推动了对体质健康评价的深入研究。本文旨在判断体重、生源地对体质健康的影响,并根据影响大学生体质健康的六大项指标:身高体重指数、肺活量体重指数、立定跳远、台阶测试、(男生)握力体重指数、(女生)坐位体前驱,建立具有代表性、科学性,实用性的体质健康综合评价模型,对大学生的体质健康进行综合评价。(详见2013年数学建模苏北赛A题,本论文中的数据也均来源于该题)。
1 体重对体质健康的影响
1.1 建模准备
1.1.1 体重指数的定义及计算公式
BMI指数(体质指数又称体重指数,英文为Body Mass Index,简称BMI),是用体重公斤数除以身高平方得出的量,是目前国际上常用的衡量人体胖瘦程度以及是否健康的一个标准。其模型为:

其中w为体重(单位:kg);h为身高(单位:m)。
1.1.2 评估等级
国际生命科学委员会中国办事处规定符合中国人的体质等级见表1:

表1 体质健康等级
我国大学生已经步入成人阶段,属于成年人群体,可以把身高体重指数的标准范围确定为18.5~24;体重指数的大小,严重影响着人的身体机能和身体素质指标的变化,直接关系到人体体质状况。
1.2 模型的建立与求解
运用Excel对学生体质测量数据进行数据间的换算、函数统计和频数分析,并用Excel中饼形图和散点图显示学生的体质健康等级分布现状[3]。
对某高校大学生 1069 人(男生764人,女生307人)的体质健康测试数据进行单独分析,得出等级分布饼形图情况如下:
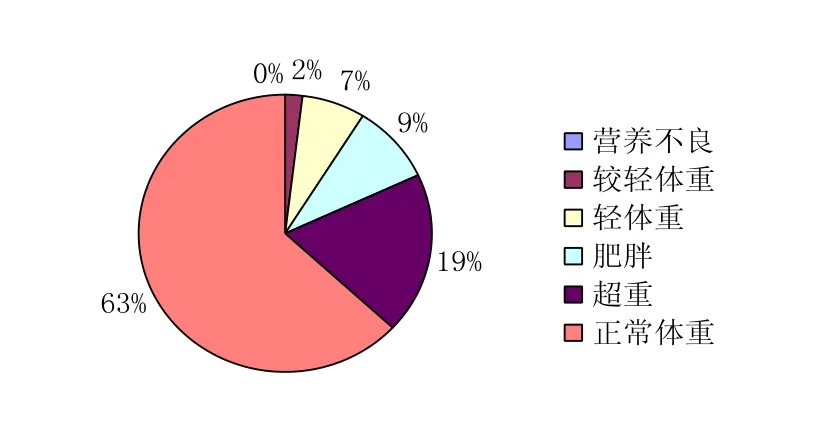
图1 高校男生 BMI 分布

图2 高校女生 BMI 分布图
图3和图4为高校大学生 BMI 等级范围的总体分布情况,总体分布状况显示如下:

图3 男生 BMI 分布图
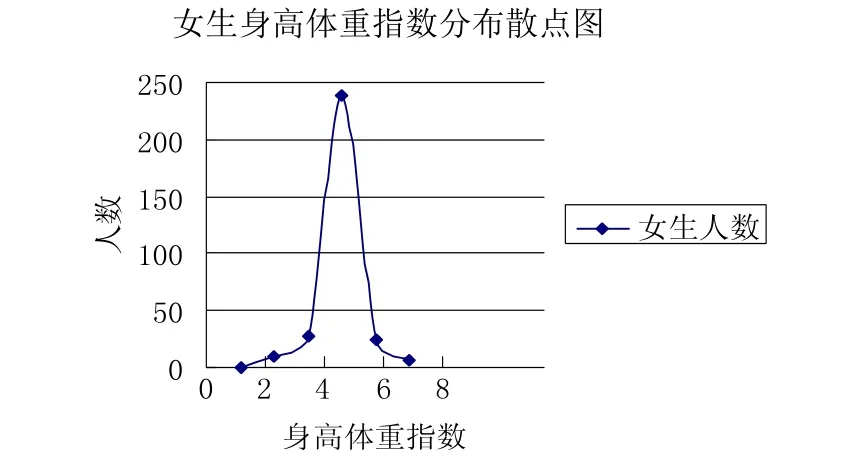
图4 女生 BMI 分布图
综合该高校大学生体质测试指标数据,对总体的BMI分布情况综合分析,结果如表2。

表2 大学生 BMI分布对比情况
1.3 结果的分析
从表2中大学生BMI分布对比情况中的数据可知:
(1)该校男、女学生的BMI在正常体重等级范围内的比例均大于60%;说明该高校大学生的BMI总体状况良好。
(2)正常体重等级范围内的百分比例值男生明显低于女生,且男生在正常体重两侧的分布不平衡,非正常体重范围中,低体重比例明显低于超重和肥胖比例,总体偏向重体重一侧,而女生的BMI在正常体重等级范围内的比例超过3/4且正常体重两侧的分布几乎持平。这说明大学生BMI值还存在很大的改善空间,特别是男生,应该注意体型过于肥胖的状况。
(3)总体上,该高校大学生中没有营养不良的情况,学生的BMI总体状况良好。但是男生有点趋于超重和肥胖,应该注意改善,否则会影响体质健康;而女生的总体状况较好,但仍然具有改善的空间。
2 剔除可能偏差测试结果
2.1 因素分析
在体质健康测试中,常会由各种因素使测试结果可能存在误差,需建立数学模型检验其准确性。有时即使通过相关系数或F检验证实回归方程可靠,也不能排除数据存在上述问题。如果对学生测试结果做MATLAB残差图分析[4],则可以很好地解决上述问题。
所谓残差是指实际观察值与回归估计值的差。显然有多少组数据,就有多少个残差。MATLAB残差分析就是通过残差所提供的信息分析出数据的可靠性。
2.2 处理步骤
(1)再利用MATLAB7.0编程可作出1,2,3班学生指标残差图。
(2)从残差图可以看出数据的残差离零点的远近,当残差的置信区间均包含零点,这说明回归模型能较好的符合原始数据,否则可视为异常点。
2.3 残差分析
对1,2,3班同学测试结果分别作残差图,有六个测试指标,编写相应MATLAB程序。得到的1,2,3班同学测试数据的残差图如图5所示(黑色代表异常数据,灰色代表正常数据):
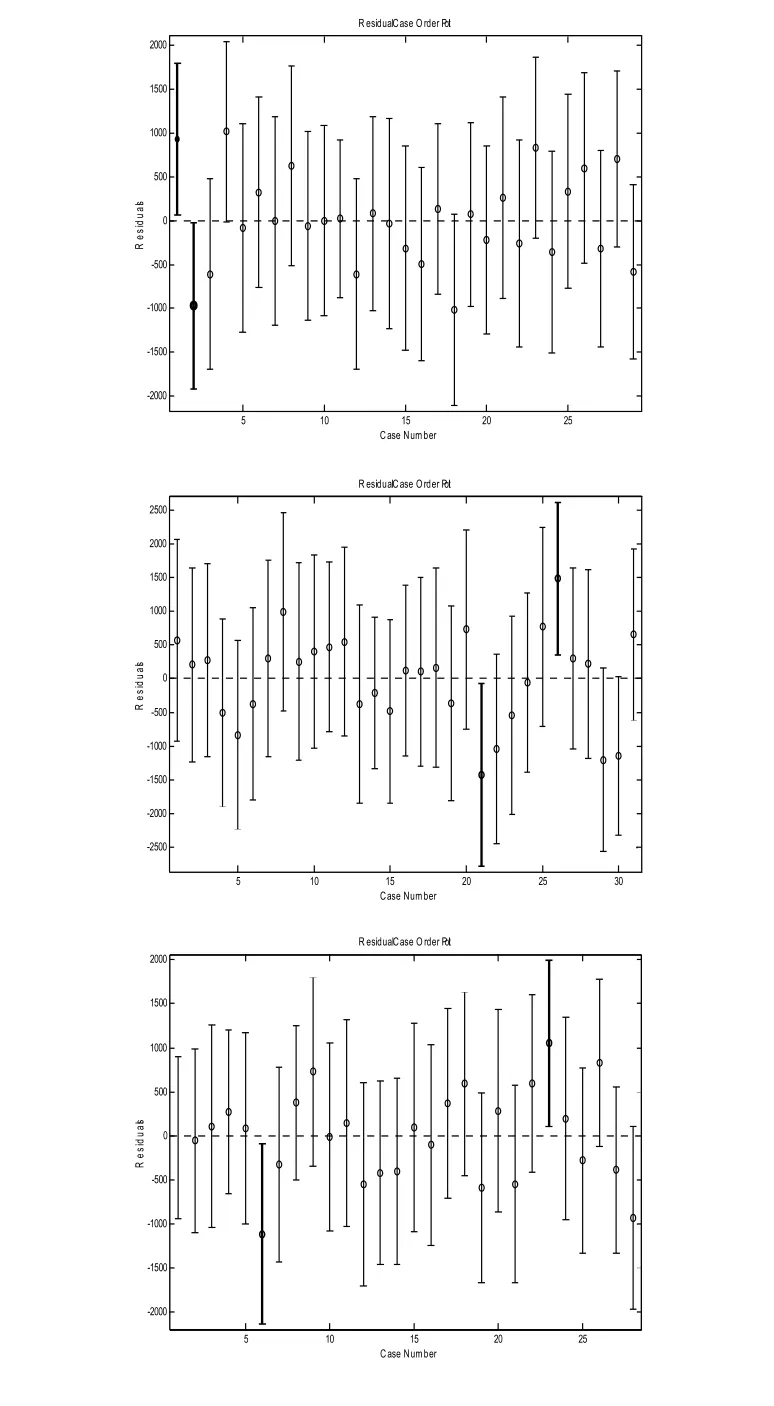
图5 1、2、3班同学测试结果的残差图
由图5中三个图可看出,1班同学中第1个同学和第2个同学的测试数据异常,2班同学中第21个同学和第26个同学的测试数据异常,3班同学中第6个同学和第23个同学的测试数据异常,因此其测试结果视为可能偏差结果。
3 生源地对体质健康状况的影响
3.1 建模准备
首先,剔除附表中的已知测量数据中的不合理的数据,采用数理统计方法对有效数据进行数据处理[5],计算出不同生源地男生女生的体重指数、肺活量体重指数,其中:肺活量体重指数:肺活量(mL)/ 体重(kg)。
然后计算各地区学生身高体重指数、肺活量体重指数、立定跳远、台阶测试、(男生)握力体重指数、(女生)坐位体前驱六大项指数的平均值。
3.2 模型的建立与求解
⑴计算不同生源地的男女生身高、体重、肺活量的平均数,然后计算不同生源地男生女生的身高体重指数平均数、肺活量体重指数平均数;结合计算出的身高体重指数、肺活量体重指数的平均值,可以得到按不同生源地划分的男生女生的五大项指数(见表3和表4)。
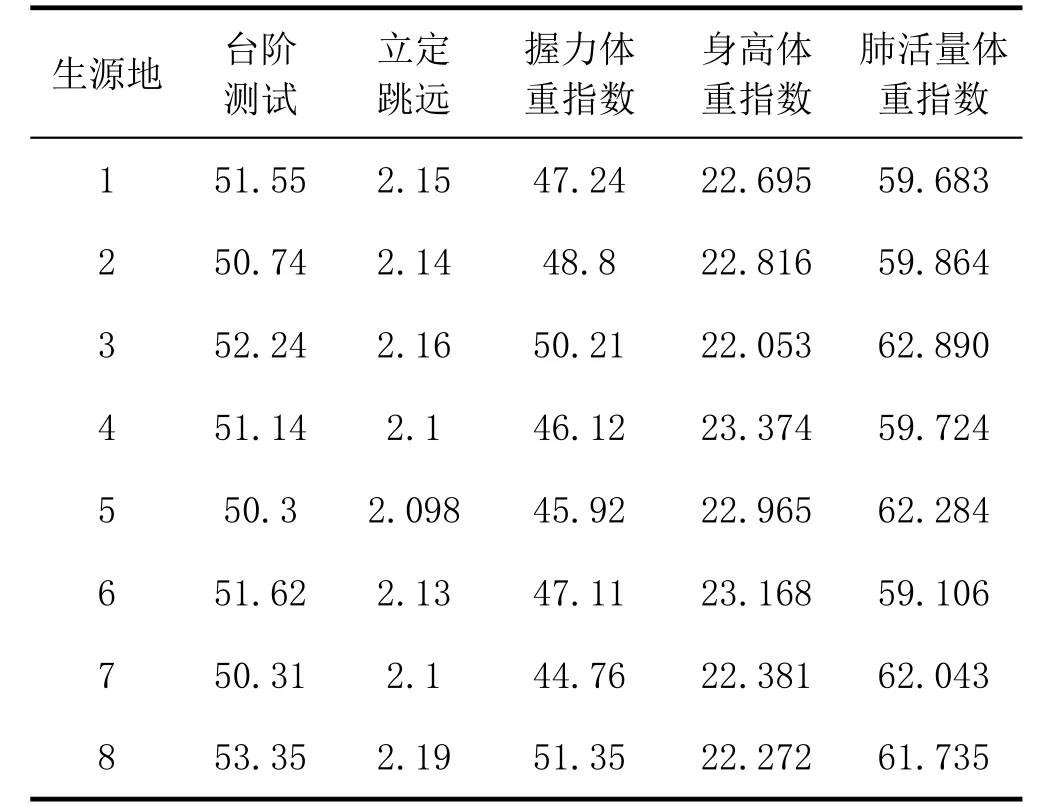
表3 不同生源地男生各项指数平均值

表4 不同生源地男生各项指数平均值
根据表3、表4计算出的各项指数的平均值,结合题目附表中已给出的大学生各项测试项目评分标准分析不同生源地的男女生健康状况,并判断其是否具有显著差异。经分析计算得出表5和表6。
由表5、表6可得出结论:生源地8的男生较其他地区的男生身体更健康,生源地4的女生较其他地区的女生身体更健康,且女生的身体健康状况普遍比男生好。故不同地区的学生的体能健康是具有一定差别的。

表5 各地区男生各项指标得分和健康等级

表6 各地区女生各项指标得分和健康等级
4 体质健康模糊综合评价
4.1 建模准备
(1)由大学生体能测试表及大学男女生各项测试评分标准可看出,进行综合评价时要考虑4个综合指标,即肺活量体重指数,台阶试验,立定跳远,握力体重指数(男生)或坐位体前屈(女生)。
(2)男女生评分标准不同,因此要把男女生分开求解,且原附表中没给出学生的肺活量体重指数,因此也要求出学生的肺活量体重指数。
(3)定义:① 向量的欧氏距离:

其中α,β为向量,d(α,β)为向量α与β之间的欧氏距离。
② 向量的绝对距离:

其中α,β为向量,d(α,β)为向量α与β之间的绝对距离。
将建模思路通过流程图表示为图6:
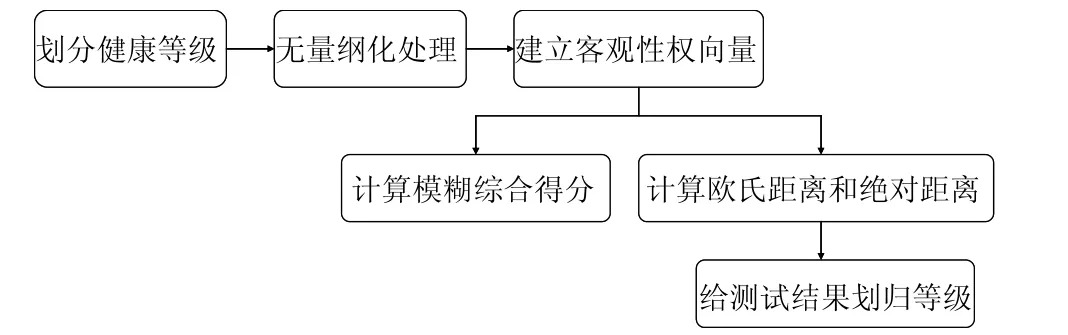
图6 体质健康模糊综合评价建模思路通过流程图
4.2 模型的建立
对1班的学生进行体能健康评价时,男女生建立的模型是一样的,因此本文只给出女生评价模型的建立方法,男生方法同女生,不再赘述。
(1)首先求得6个女生的4项评价指标测试结果的指标矩阵 A(aij),i=1…6,j=1…4,其中 aij为第i个女生的第j项指标的测试结果。并把女生测试评分标准表中的4项指标整体考虑,把健康评价指标分为21个等级,从上到下分别为优秀1,优秀2,……,优秀6,良好1,良好2,……,良好5,……,不及格1,不及格2,……,不及格5。可得到这21个等级的评价指标值矩阵B(bij),其中bij为第i个等级的第j项指标的值。
(2)显然这4个指标的单位不同,针对这4个指标建立可建立效益型矩阵或成本型矩阵,为了迎合大家习惯,这里通过无量纲化处理,将矩阵A和B的各元素均转化为效益型指标,得出的综合评价得分为越大越好。转化方法为 ,转化后可得到无量纲[5]同属性的指标矩阵C和D。
(4)计算矩阵C中各女生的指标向量与矩阵D中各个等级的指标向量的欧氏距离和绝对距离,离哪个等级指标向量最近即可将其化为该等级。
4.3 模型的求解
4.3.1 对1班女生求解
(1)由6个女生的4项评价指标测试结果得出指标矩阵A,由女生21个评价等级的4项评价指标值得出指标矩阵B。

(2)利用MATLAB7.0编程,将矩阵A和B无量纲化后得到矩阵C和D。利用变异系数法求得权向量,再利用权向量求得相对综合评价得分。利用MATLAB7.0编程,求得矩阵C中各女生的指标向量与矩阵D中各个等级的指标向量的欧氏距离和绝对距离,再将欧氏距离和绝对距离从小到大排名。两种距离求得的结果相差很小,说明这种求距离方法的可靠性。本文选择欧氏距离的结果作为最终女生综合评价等级结果。
(3)由6欧氏距离可看出6个女生的相应综合评价等级。
4.3.2 对1班男生进行求解
(1)由23个男生的21项评价指标测试结果得出指标矩阵A,由男21个评价等级的4项评价指标值得出指标矩阵B。
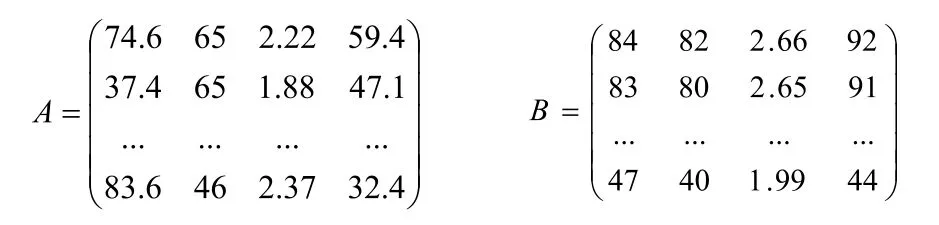
(2)利用跟女生相同的求解方法,进行MATLAB编程求解。
(3)由相应的欧氏距离可看出23个男生的相应综合评价等级。
4.3.3 结果
综合6个女生的相应综合评价等级和23个男生的相应综合评价等级,可得到1班的所有学生的体质综合评价等级如表7。
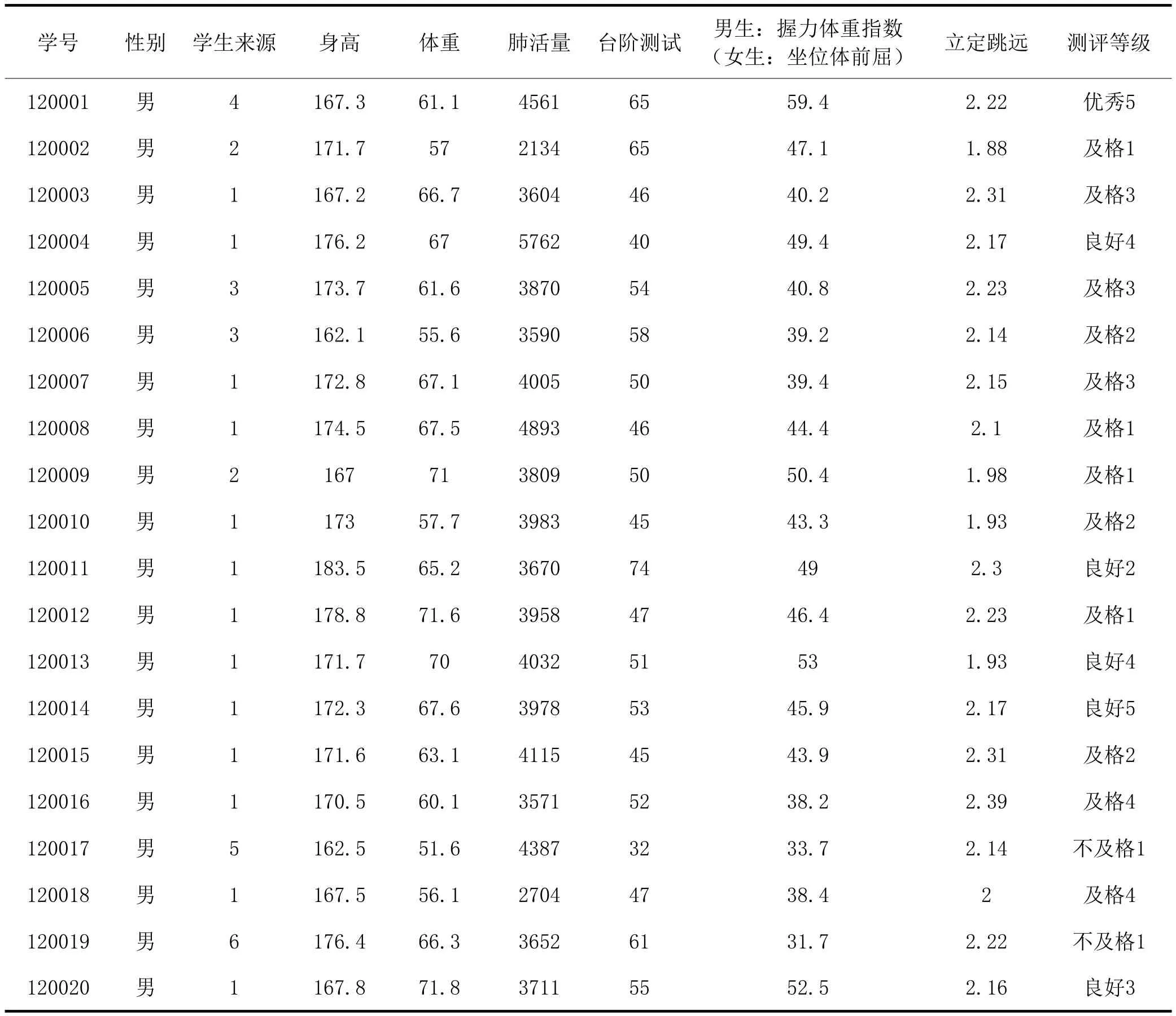
表7 1班学生体质等级
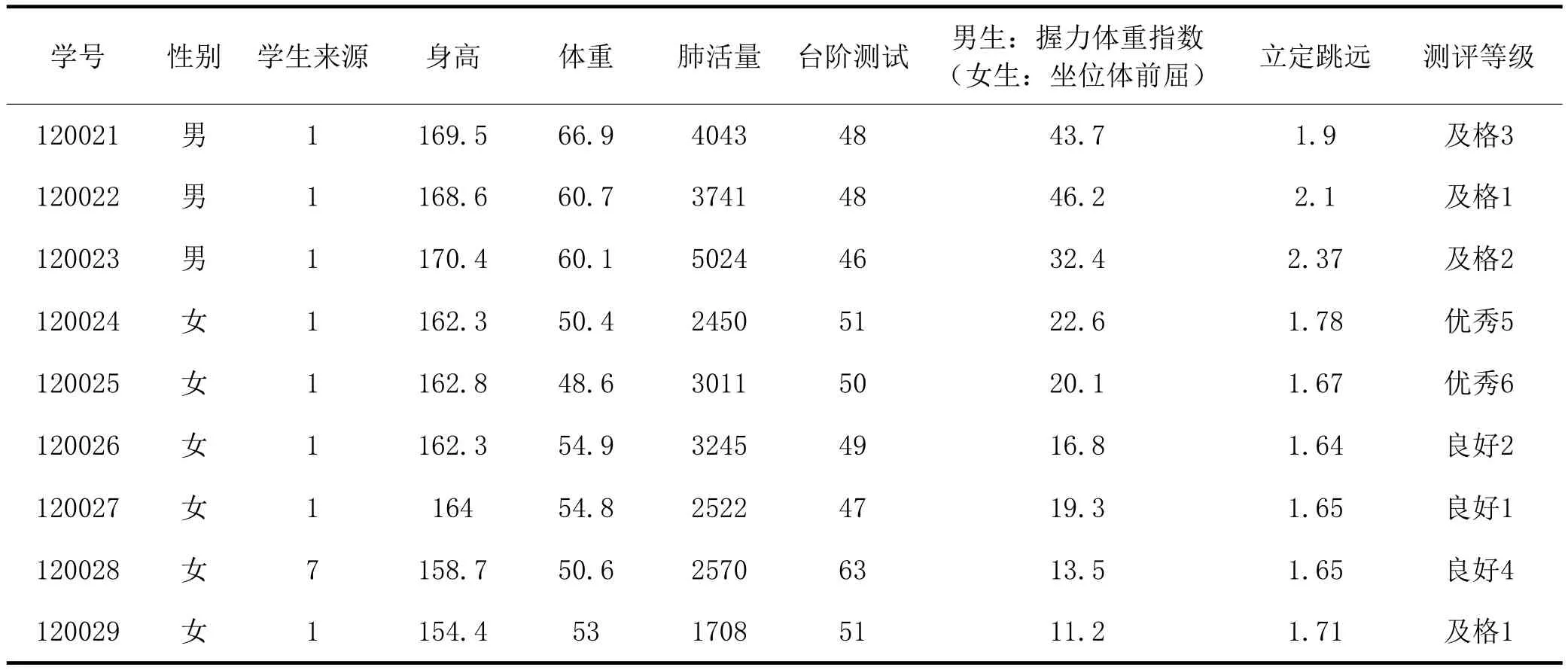
表7 (续) 1班学生体质等级
由表7可得,1班同学的不及格率为2/29≈6.9%;及格率为27/29≈93.1%,其中体质良好同学所占比例为8/29≈27.6%,体质优秀同学所占比例为3/29≈10.3%。
5 结语
以上各模型在建模过程中通过检验,具有一定的合理性。得出了体重、生源地对健康的影响,找出了可能偏差测量结果,在求每个学生的测试结果的应属等级时采用了不同的方法,运用软件进行计算使得结果更加准确,对1班每个学生的体质健康作出了综合评价。
[1]林静,王建雄.美国体制研究发展等若干问题讨论[J].天津体育学院院报,1997(3):21-24.
[2]日本文部省2000年最新体质测定办法[J].大众体育信息,2001(4):6-9.
[3]杨世莹.Excel数据统计与分析范例应用[M].北京:中国青年出版社,2004:75-97.
[4]谢中华.MATLAB统计分析与应用:40个案例分析[M].北京:北京航空航天大学出版社,2010:81-109.
[5]杨桂元,黄己立.数学建模[M].合肥:中国科技大学出版社,2008:154-158.
