致密气藏水平井压裂产能预测研究

2014-10-24任登峰王亚娟李年银古永红

天然气勘探与开发 2014年2期

马旭任登峰王亚娟李年银古永红

（1.中国石油长庆油田公司油气工艺研究院 2.“油气藏地质及开发工程”国家重点实验室·西南石油大学）

对于低渗、特低渗油气田，通常采用水平井并进行压裂的方法来提高油气产能，压裂产能预测的准确性直接影响压裂设计和压裂经济评价。前人对水平井压裂产能预测做了大量的研究[1-12]，但大多是针对射孔完井方式[1-3,5-6,10-11]，而水平井裸眼完井方式下压裂产能预测模型较少[8-9]，而且大多仅考虑了多裂缝系统中裂缝之间的相互干扰，而没有考虑裂缝和裸眼井段之间的相互干扰，这和实际不符。本文将任意两条裂缝之间的裸眼井段处理为等效裂缝，和人工裂缝做同样的离散化处理并根据复位势理论、势的叠加原理建立了水平井裸眼完井压裂油藏渗流模型和井筒管流耦合模型，研究分析了裂缝参数对压裂水平井产能的影响规律。

1 压裂水平井产能模型的建立

1.1 水平井分段压裂流态分析

水平井采用射孔完井时，井的产能仅是由裂缝提供（图1a）。由于裂缝长度远大于裂缝高度，裂缝的渗透率远大于基质的渗透率，故不考虑基质中流体的垂向渗流过程。

针对裸眼完井的水平井分段压裂，井筒完全暴露在气藏中，因此裂缝和气藏都是持续向井筒供液的（图1b）。由于裂缝之间的相互干扰以及气藏直接向井筒的供液使得问题变得复杂。

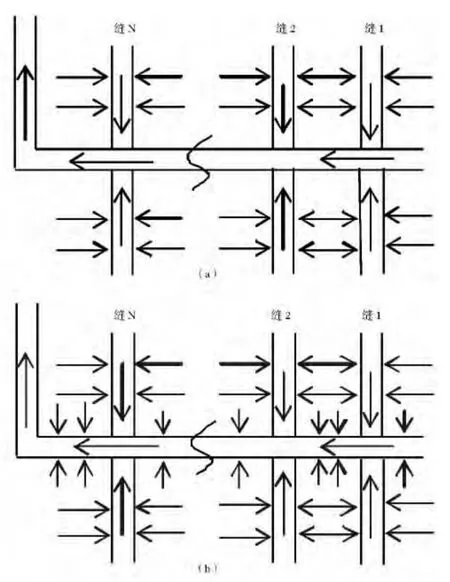
图1 水平井不同完井方式下分段压裂流态示意图

1.2 产能预测数学模型推导

水平井裸眼完井分段压裂流体的流动形式不同于射孔完井。在裸眼完井的情况下，水平井筒完全暴露在气藏中，裂缝和基质都是产能的贡献源，这涉及到两个流动过程：基质—裂缝—井筒的双线性流、基质向井的径向流。所以在进行压裂产能模拟时，要充分考虑这两个过程以及相互之间的干扰。

（1）基质-裂缝-井筒双线性流模型

在多裂缝系统中，将每条裂缝的左右两翼分别n等份，每一等份作为点汇来处理；由于裂缝和井筒在接受流体的过程中具有相似点，以及为了和裂缝系统共用同一坐标系，如图2所示，根据面积相等的原则，将任意两条裂缝之间的井筒视△xi为厚度为πrw（其中rw为井筒的半径），长度为△xi的等效裂缝，并对其n等份，每一等份视为点汇来处理。

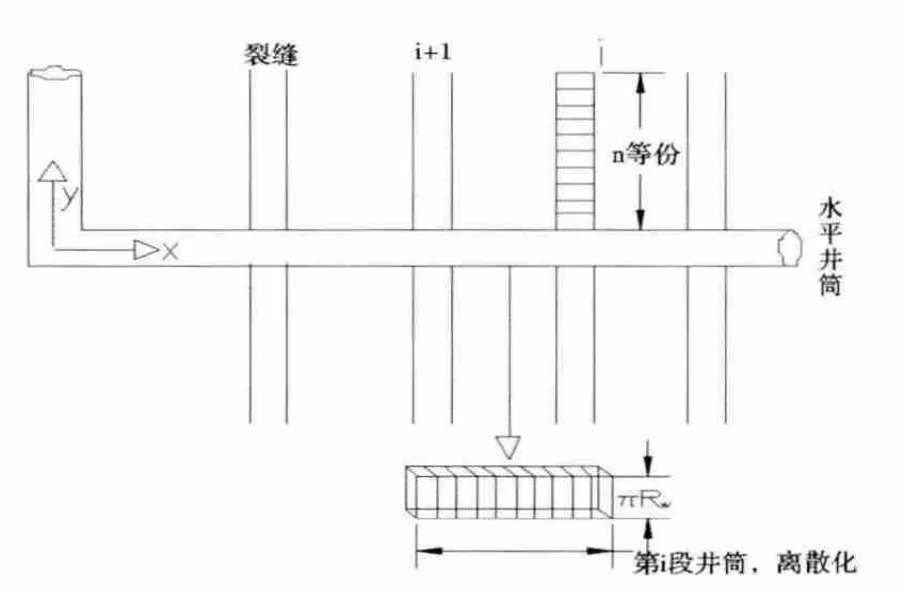
图2 水平井裸眼完井分段压裂物理模型

地层中任意一点的压降计算以无限大均匀地层的点汇定流量压降为基础，考虑N条裂缝和N+1段裸眼井筒之间相互干扰时在地层中任意一点(x,y)处压降计算公式为：

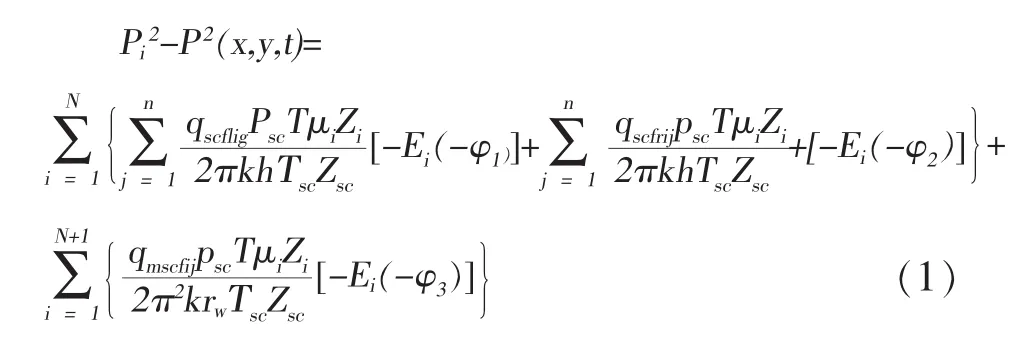
式中：

假设第k条裂缝的左、右翼尖端坐标分别为(xfkl,yfkl)、(xfkr,yfkr)，压力分别为Plk和Prk，长度分别为yflk和yfrk。将第k条裂缝的左、右翼尖端坐标代入（1）式即可求得左右翼尖端压力。当裂缝不对称分布时可取左、右翼尖端压力的平均值作为第i条裂缝的尖端压力。

由于裂缝半长远大于水平井筒半径，所以可将任意两条裂缝和对应井筒的渗流过程根据面积相等的原则视为半径为R，厚度为h，外边界压力为裂缝尖端压力P(xfi,yfi,t)，内边界压力为井底流压Pwfi的微型气藏。其中：

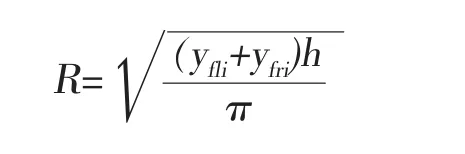
则可知裂缝内气体的渗流公式为:

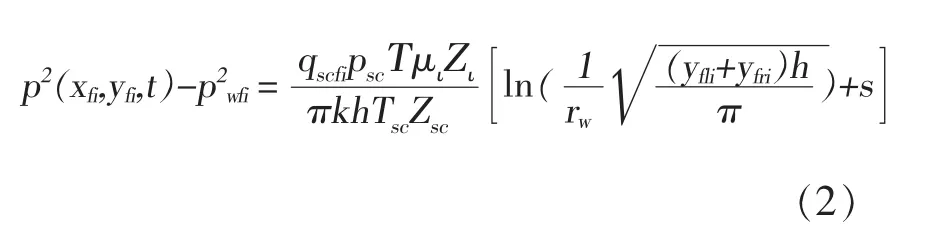
由裂缝的左右翼尖端压力和式（2）联立可得出考虑裂缝和裸眼井段之间相互干扰的基质-裂缝-井筒双线性流模型。

（2）基质向井流动模型

根据式（1）在井筒的末端和每条裂缝与水平井筒的交点处建立方程。第i条裂缝与井筒的交点坐标为 (xi,0)、井筒末端的坐标为 (L,0)（L为水平井段长度）。

在这N+1个点处建立方程可得出考虑裂缝和裸眼井段之间相互干扰的基质向井流动模型。

（3）井筒压降模型

根据质量守恒原理和动量定理，可导出水平井筒内某段流动压降[12]：

则上式可化简为：

（4）裂缝系统模型和井筒模型的耦合求解

将上面得出的基质-裂缝-井筒的双线性流模型和基质向井流动模型分别和井筒压降模型耦合即可构成2N+1个方程（式5），每个方程具有2N+1个变量，采用牛顿迭代法求解，根据时间步长，即可求得任一时间每条裂缝产量、基质产量以及水平井的平均产量和累计产量。

2 模拟结果分析

2.1 射孔和裸眼完井方式下压裂水平井产能对比

裸眼完井压裂水平井在生产初期产量较高，而射孔完井压裂水平井的产量较低（图3）；但进入稳定或拟稳定阶段之后，两种完井方式对应的压裂水平井的产量基本一致。原因是：生产初期，水平井筒周围能量比较集中，基质首先向井筒供液，而此时岩块正向裂缝补给流体，裂缝中的流体尚未到达水平井筒。因此，对于裸眼完井来说在生产初期沿井筒方向流体流入是不可忽视的。

图3 射孔完井和裸眼完井方式下水平井产能对比

2.2 裂缝参数分析

利用前面推导的水平井压后产能预测模型，利用Matlab编程实现模型求解，对长庆某气井的相关数据进行模拟计算，具体数据见表1。

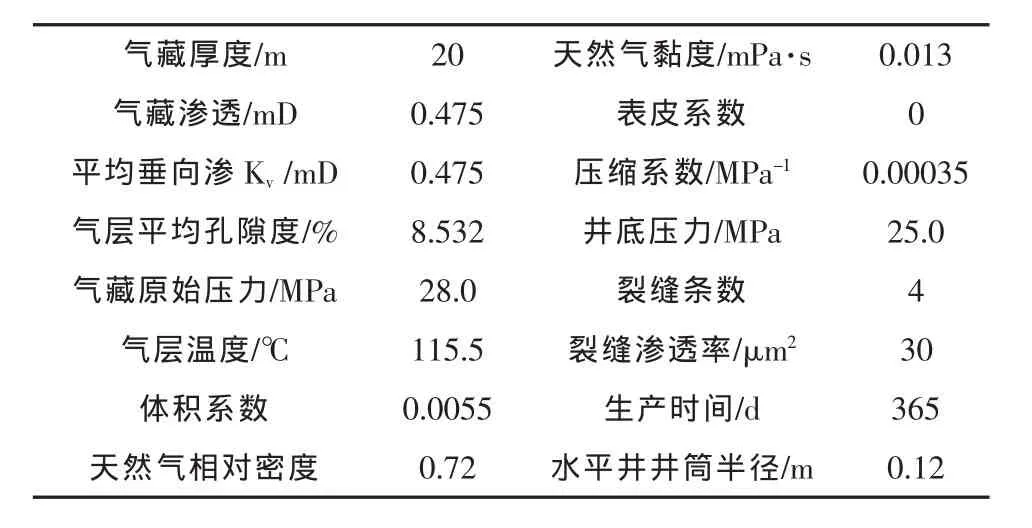
表1 长庆某井气层与流体物性参数

（1）裂缝平面与水平井井筒夹角

随着裂缝夹角的增加，压裂水平井累计产量逐渐增加，但随着夹角的不断增大产量增幅会不断的减小（图4）。从图中可以看出夹角为90°时水平井产量最高，所以对于低渗致密气藏水平井，压裂多段横切裂缝的效益要优于其它角度的裂缝。

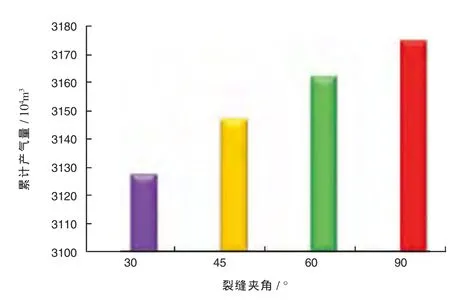
图4 裂缝夹角对累计产量的影响

（2）裂缝条数、裂缝长度、裂缝导流能力

裂缝条数、裂缝长度、裂缝导流能力对气井产量的影响趋势是相同的，即随着上述因素的增加，气井的产量是增加的，但增加到一定程度之后，增加的幅度减小，即从经济的角度考虑存在最优范围。对于低渗、特低渗气藏，裂缝的渗透率对产能的影响不明显（图5、图6、图7）。

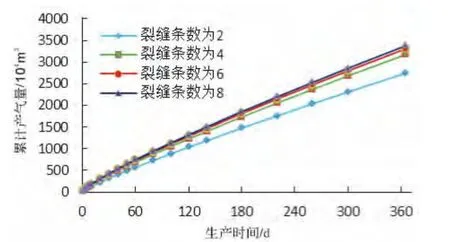
图5 裂缝条数对累计产量的影响

图6 裂缝半长对累计产量的影响

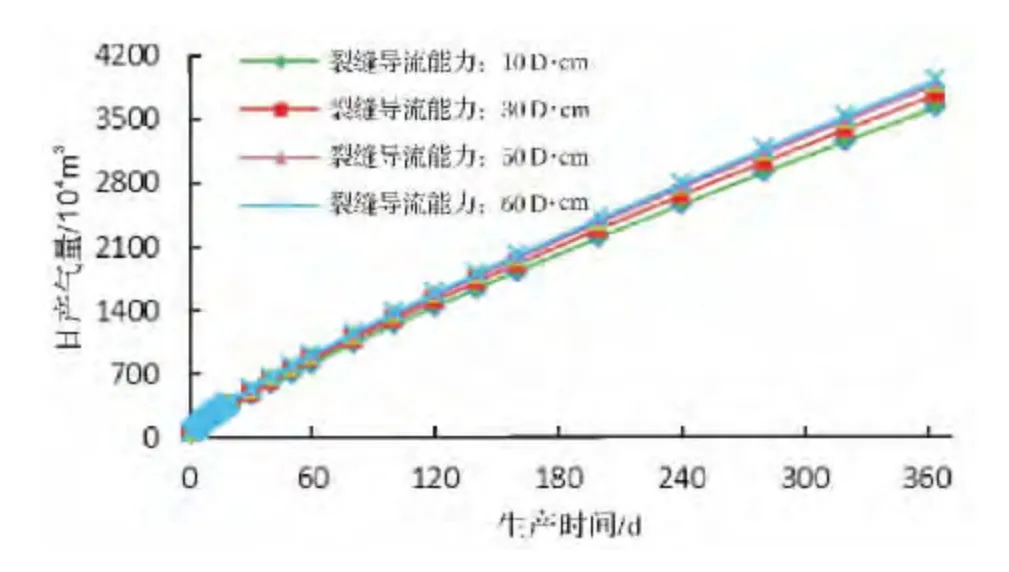
图7 裂缝导流能力对累计产量的影响

（3）不同水平段长度时裂缝条数优化

在特定的裂缝条数下，压裂水平井的产能随水平段长度的增加而增加，但随水平井长度的增加，产量增加的幅度逐步下降（图8）。另外从图中可以看出，当水平段长度较短时，裂缝条数的增加对产能影响不大；随着水平段长度的增加，裂缝条数对产能的影响逐渐增大。

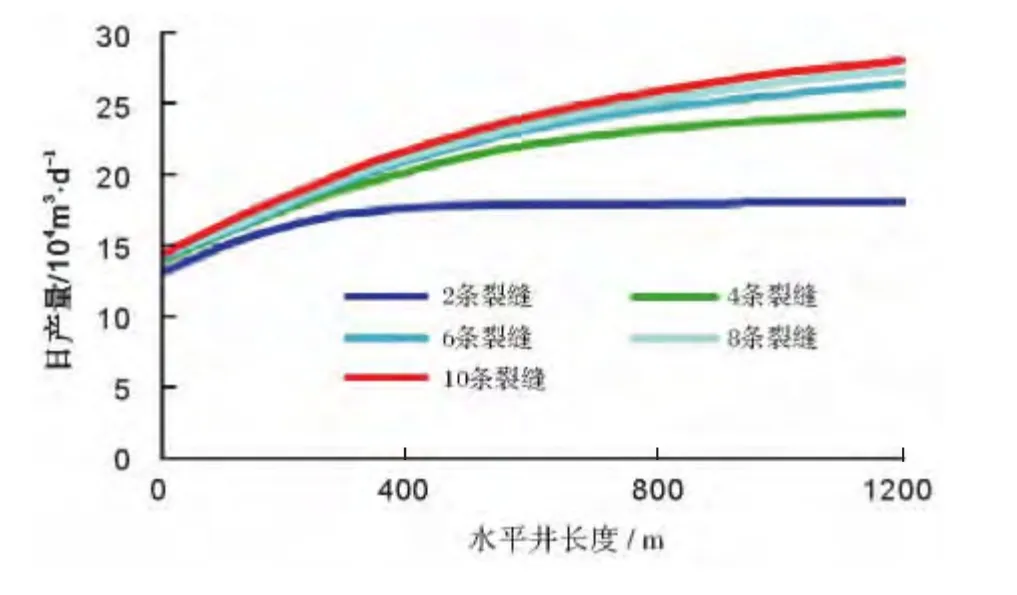
图8 不同裂缝条数下的水平井长度对产能的影响

（4）裂缝位置

裂缝1和4的产量远高于中间裂缝2和3，几乎是中间产量的两倍。在压裂施工时，为了发挥两端裂缝的优势，可适当增加两端裂缝的长度（图9）。

图9 不同位置裂缝的产量随时间的变化

3 结论

（1）在不稳定渗流的基础上，根据裂缝和井筒之间的共同点，对人工裂缝和裸眼井段做相同的离散化处理，得出水平井裸眼完井压裂产能预测模型，该模型考虑了多条裂缝和裸眼井段之间的相互干扰，也考虑了水平井井筒压降，使计算结果更符合实际。

（2）在储层条件与施工工艺相同的条件下，水平井裸眼完井压裂产能高于射孔完井，并且裂缝渗流始终占主体地位，但在生产初期，井筒径向渗流不能忽略。这两种完井方式对产能的影响仅在生产初期有所不同，稳定或拟稳定阶段基本一致。

（3）增加裂缝的条数、长度、间距、裂缝与水平井筒的夹角等因素都对压裂井的产能具有积极的影响，但是考虑到经济因素，这些因素存在最佳的范围，同时，对于低渗、特低渗气藏，裂缝的渗透率以及裂缝平面与水平井井筒夹角对产能的影响不明显；两端裂缝的产量几乎是中间裂缝产量的两倍，为了充分发挥两端裂缝的优势，建议压裂时裂缝长度呈“U”型排列。

符号说明

N—裂缝条数；

A—油井的泄油面积，m2；

D—井筒直径，m；

μ—地层流体的黏度，mPa·s；

k—储层渗透率，D；

h—储层的厚度，m；

T—气体的温度，K；

γg—气体的比重；

ff—摩擦因子；

pi—原始地层压力，MPa；

p（x,y,t）—地层中任意一点（x,y）在t时刻的压力，MPa；