斜直井段套管-水泥环组合系统受力特性分析

王宴滨，高德利，房 军

(中国石油大学石油工程教育部重点实验室，北京 102249)

对于直井段套管－水泥环－地层组合系统的受力特性问题已做过大量的研究，为正确认识套损问题提供了丰富的依据［1-5］，然而实际情况中存在着大量的斜直井段，理论上的直井在实际中也不可能是绝对的垂直井，总存在一定的井斜角［6］，因此将直井段得出的规律应用在斜井段时受到了限制。笔者采用坐标变换的方法从理论上研究斜直井条件下套管－水泥环－地层组合系统的受力特性，以得到斜井段下套管的外挤力分布，为正确认识斜井段套管的损坏问题及采取合理的预防套损措施提供参考。

1 应力张量的坐标变换与分解

1.1 应力张量的坐标变换

在油田地应力分析中，通常将地应力用3个主应力表示，即上覆岩层压力σv、最大水平主应力σH和最小水平主应力σh。σv的方向为竖直向下，而σH和σh在不同的地域方向不同，且通常使用井壁崩落法、岩心差应变试验、水力压裂法等方法进行测量［7-8］。

选择初始坐标系(X，Y，Z)分别与主地应力σH、σh和 σv方向相反，并建立直角坐标系(x1，y1，z1)、(x，y，z)和(r，θ，z)，其中 oz轴对应于井眼轴线方向，ox和oy位于与井眼垂直的平面内，如图1所示。

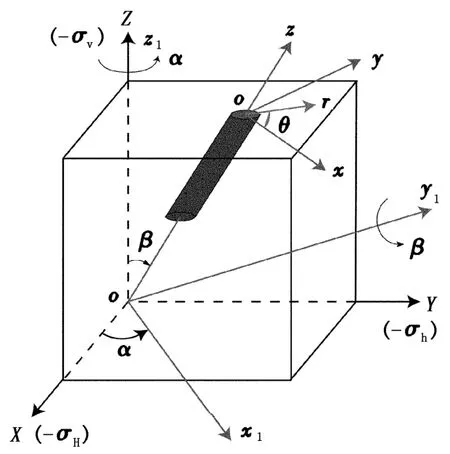
图1 斜井-直井井轴坐标变换图Fig.1 Coordinate transformation of inclined-vertical well shaft

为了建立(x，y，z)坐标系与(X，Y，Z)坐标系之间的转换关系，将(X，Y，Z)坐标系按以下方式［7-8］旋转:

(1)先将坐标系(X，Y，Z)以Z为轴，按右手定则旋转角度α，变为(x1，y1，z1)坐标系。α为井斜方位角，指井眼轴线在水平面上的投影与正北方向的夹角。

(2)再将坐标系(x1，y1，z1)以 y1为轴，按右手定则旋转角度β，变为(x，y，z)坐标系。β为井斜角，指井眼轴线与铅垂线之间的夹角。

则坐标系(x，y，z)与初始坐标系(X，Y，Z)之间的坐标转换关系为

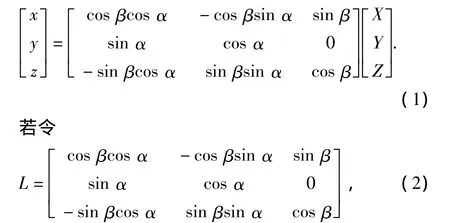
则新坐标系下的地应力张量与原地应力之间的关系为

1.2 应力张量的分解

地层中一定深处的套管，其纵向变形受到限制，如不考虑外载(地应力)沿纵向的变化可将此问题处理成平面应变问题加以分析［3］，如图2所示。因此可以忽略应力张量σ沿z轴方向的分量，得新的应力张量T，即

并将T作如下分解:

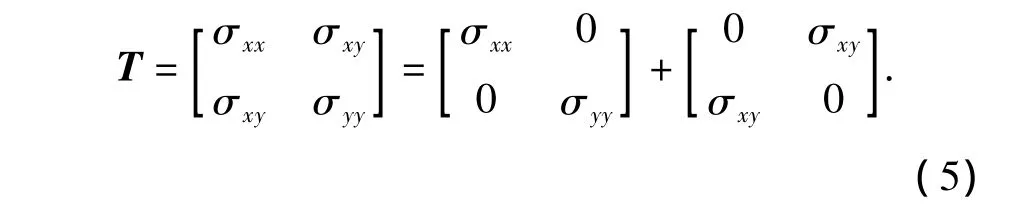
分别令

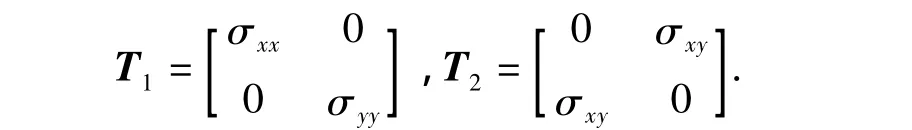
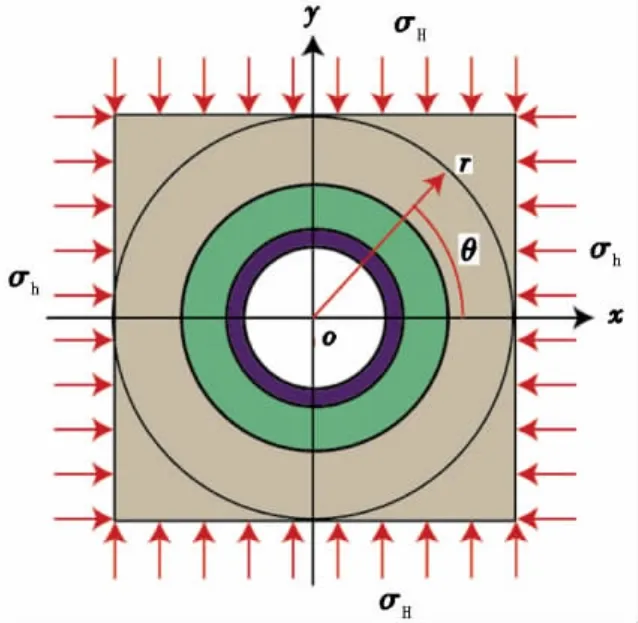
图2 套管-水泥环-地层系统平面应变分析模型Fig.2 Plane strain analysis model of casing-cement ring-formation

对于T1，分析方法与垂直井眼在水平主应力作用下的分析相同，具体推导见文献［3］。

对于T2，转换成极坐标系下的应力表达式为

式(6)与垂直井下的表达式不同，因此须以此应力张量为边界条件对系统受力进行新的分析计算。

在得到T1和T2两个应力边界条件下的套管的外挤特性之后，将其叠加即可得斜直井地层－水泥环－套管系统在原场地应力下的套管外挤力。

2 套管外挤力响应

2.1 系统在T1下的套管外挤力响应

系统在T1应力下的外挤力响应与垂直井在两向水平主应力作用下的分析相同，参见文献［3］。

2.2 系统在T2下的套管外挤力响应

考虑到地层远场应力的边界条件(σr=σxysin(2θ))的形式，取应力函数形式为

式中，φ应满足应力协调方程，因此待定函数f(r)应满足

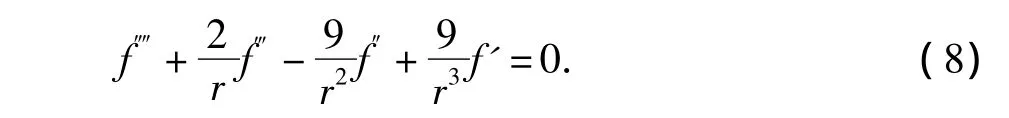
式(8)为一个四阶欧拉常微分方程，其通解为

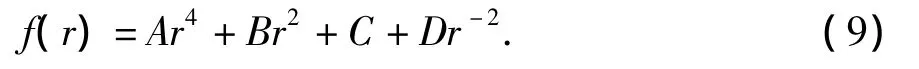
即

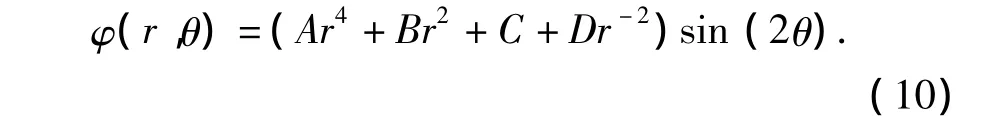
将式(10)代入极坐标系下基本方程，并分别以下标i=1，2，3表示套管、水泥环、地层，可得到系统在T2下的套管外挤力表达式为

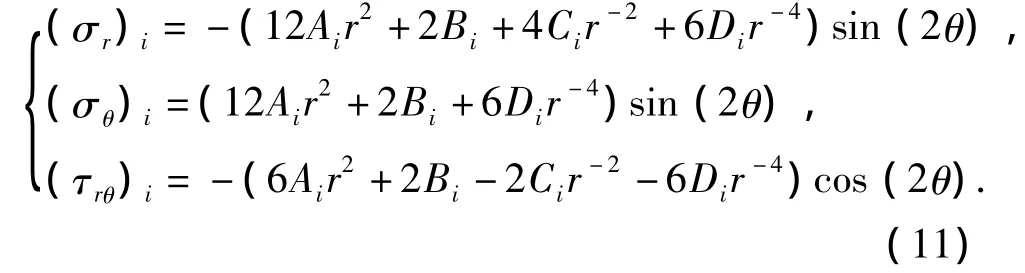
式(11)中共有12个未知参数，需要12个方程才能求解。其中应力边界条件和连续条件与T1类似，可得6个方程［3］，唯一不同在于地层外边界上的应力边界条件:

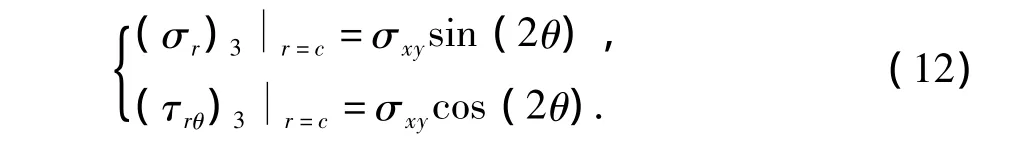
将上述8个应力边界条件代入式(11)可以得到8个方程，另外4个位移连续条件需要经过位移分析后由位移连续条件确定。经位移分析之后，得到在T2应力场作用下系统的位移方程可表述为

联立各应力边界与连续条件以及位移连续条件可得到12个方程，能够唯一确定式(11)中的12个未知量。

方程的矩阵形式为

其中

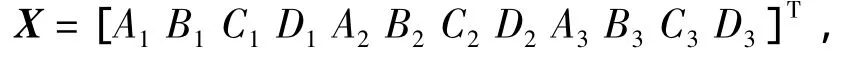
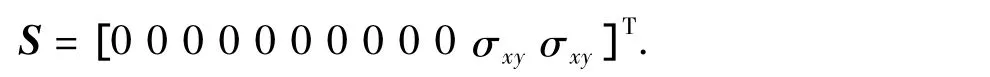
A是与系统各力学参数及几何参数有关的物理量，求解式(14)得到系数X，将得到的计算系数代入式(11)即可得到系统在应力场T2下的应力分布。

3 算例分析

参考某油田1.0 km深处地层情况的计算结果［3，11］。具体参数为:套管直径 139.7 mm，壁厚7.72 mm，水泥环厚度50 mm;地层计算厚度取3.0 m;力学参数取 E1=2.1 ×105MPa，μ1=0.25，E2=1.1 ×104MPa，μ2=0.25，E3=2.8 × 104MPa，μ3=0.30，方位角30°。计算的地层3个主应力间的关系见表1。

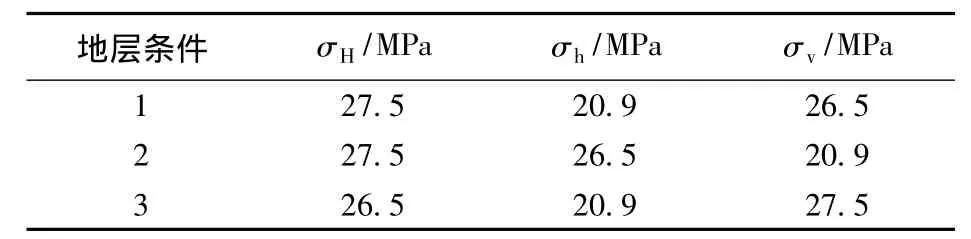
表1 3种条件下地层主应力Table 1 Three cases of formation principal stress

以井斜角30°为例，得到的地层1条件下套管－水泥环及水泥环－地层两接触表面的接触应力如图3所示，为了计算不同井斜角对套管－水泥环表面接触应力的影响，在其余条件不变的情况下，将井斜角由0°逐渐增加到90°，即在井由直井逐渐变化到水平井过程中，得到的3种地层条件下套管－水泥环表面的接触应力与井斜角的关系分别如图4所示。

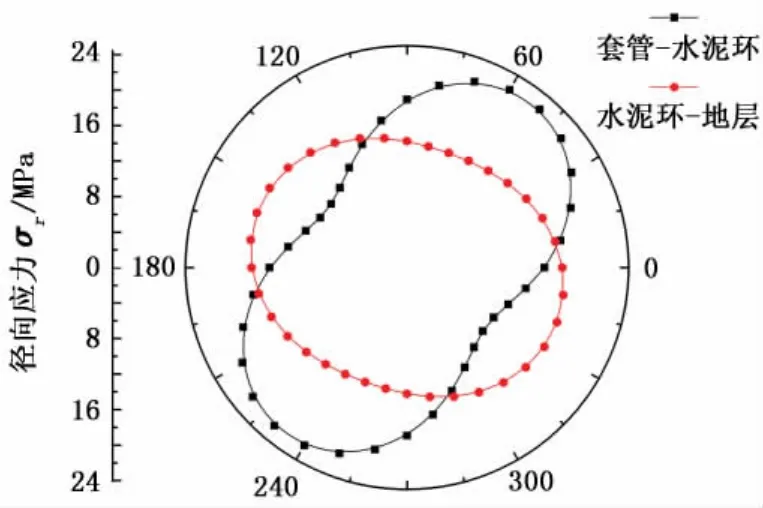
图3 地层1条件下两接触表面的应力分布Fig.3 Stress distribution of two contact surfaces in formation 1

从图3中可以看出，本算例中在地层1条件下套管－水泥环界面与水泥环－地层界面的接触应力均呈椭圆形分布，并且前者应力分布的非均匀性要大，对套管的安全不利，两者的应力幅值出现的相位差约为50°。

从图4可以看出，本算例中3种地层条件下的套管－水泥环界面接触应力分布规律各不相同，原因在于3种地层条件下地层3个主应力间的关系不同。地层1与地层3条件下井斜角从0°变化到90°时，套管外表面径向应力的非均匀性逐渐减小，套管的抗外挤能力逐渐增强，即在这种地层条件下水平井的套管抗外挤能力要大于同等条件下直井的套管抗外挤能力;地层2条件下，井斜角从0°变化到90°时，套管外表面径向应力的非均匀性逐渐增大，套管的抗外挤能力逐渐降低，即在这种地层条件下水平井的套管抗外挤能力要小于同等条件下直井的套管抗外挤能力。

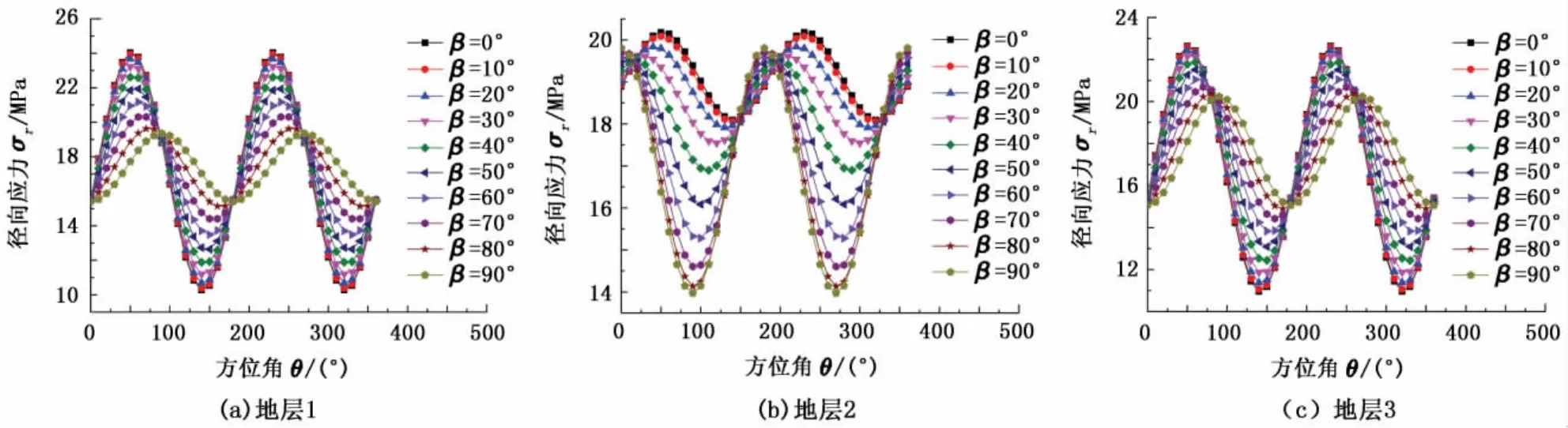
图4 套管-水泥环界面应力随井斜角的变化Fig.4 Variation of stress distribution on casing-cement surface with inclined angle

4 结论

(1)通过坐标变换将地层的3个主应力变换到斜直井轴线方向与垂直于井眼轴向的平面所确定的坐标系上，可用来分析斜井条件下套管－水泥环－地层组合系统的受力特性。

(2)地层3个主应力大小关系不同时得到的斜直井下套管－水泥环界面的径向接触应力随井斜角的变化规律不同，在某些地层下水平井的套管抗外挤能力要大于同等条件下直井的套管抗外挤能力，而在另一些地层下直井的套管抗外挤能力要大于同等条件下水平井的套管抗外挤能力。

［1］ KHALAF F，CARIO U.Increasing caing collapse resistance against salt-induced loads［R］.SPE 13712，1985.

［2］ EI-SAYED A H，KHALAF F，CARIO U.Resistence of cemented concentic casing string under nonuniform loading［R］.SPE 17927，1989.

［3］ 房军，赵怀文，岳伯谦，等.非均匀地应力作用下套管与水泥环的受力分析［J］.石油大学学报:自然科学版，1995，19(6):52-57.FANG Jun，ZHAO Huai-wen，YUE Bo-qian，et al.A-nalysis of sheath loading property of casing and cement under nonuniform geologic stress［J］.Journal of the University of Petroleum，China(Edition of Natural Science)，1995，19(6):52-57.

［4］ 房军，岳伯谦，赵怀文，等.非均匀地应力作用下套管和水泥环表面受力特性分析［J］.石油大学学报:自然科学版，1997，21(1):46-48.FANG Jun，YUE Bo-qian，ZHAO Huai-wen，et al.analysis of surface loading on casing and cement sheath under nonuniform geologic stress［J］.Journal of the Uniuersity of Petroleum，China(Edition of Natural Science)，1997，21(1):46-48.

［5］ 房军，谷玉洪，米丰珍.非均匀载荷作用下套管挤压失效数值分析［J］.石油机械，1999，27(7):34-37.FANG Jun，GU Yu-hong，MI Feng-zhen.A numerical analysis of casing collapse under nonuniform load［J］.China Petroleum Machinery，1999，27(7):34-37.

［6］ 高德利，刘希圣，徐秉业.井眼轨迹控制［M］.东营:石油大学出版社，1994.

［7］ 陈勉，金衍，张广清.石油工程岩石力学［M］.北京:科学出版社，2008.

［8］ 郭春华.井眼应力分布模拟及井壁稳定性研究［D］.成都:成都理工大学环境与土木工程学院，2011.GUO Chun-hua.Simulation of in-situ stress near wellbore and research on wellbore stability［D］.Chengdu:Environment and Construction Engineering Institute of Chengdu University of Technology，2011.

［9］ 李志明，殷有泉.油水井套管外挤力计算及其力学基础［M］.北京:石油工业出版社，2006.

［10］ 徐芝纶.弹性力学:上册［M］.北京:人民教育出版社，1978.

［11］ 李宏，谢富仁，王海忠，等.乌鲁木齐市断层附近地应力特征与断层活动性［J］.地球物理学报，2012，55(11):3695-3696.LI Hong，XIE Fu-ren，WANG Hai-zhong，et al.Characteristics of in-situ stress measurements near the fault and fault activity in Urumqi city［J］.Chinese Journal of Geophysics，2012，55(11):3695-3696.