一阶超前中立微分方程解的存在性

简林祥

（福建农林大学 计算机与信息学院，福建 福州 350002）

从1836年Sturm研究热传导方程提出二阶线性常微分方程

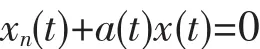
的振动问题以来，常微分方程的振动理论已经有很久的历史了，Sturm的比较定理、Sturm零点分离定理已经被写入大学教科书。Swanson[1]总结了线性常微分方程振动理论的经典结果，见文献[2]。

对于滞后的一阶中立型微分方程

其中 P(t)≡1,Q(t)∈C（[t0,∞),R+,τ,δ∈(0,∞)。

方程已有的结果是[3]:方程(1)存在有界正解的充分必要条件是

但是对于超前一阶中立微分方程的情况是否有相似的结果是未知的。

本文研究了超前一阶中立微分方程：

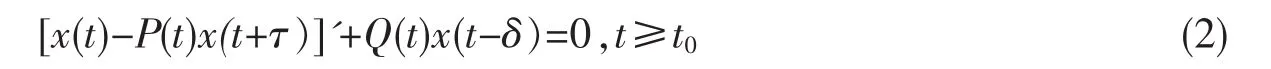
其中 P(t)≡1,Q(t)∈C（[t0,∞),R+,τ,δ∈(0,∞) 。

需要指出，在必要性的证明过程中，本文加入了条件 0＜α≤x（t）≤β，其中 x（t）为方程(2)的有界正解。

1 结果及证明

引理1方程(2)存在有界正解的充分必要条件是

现定义函数

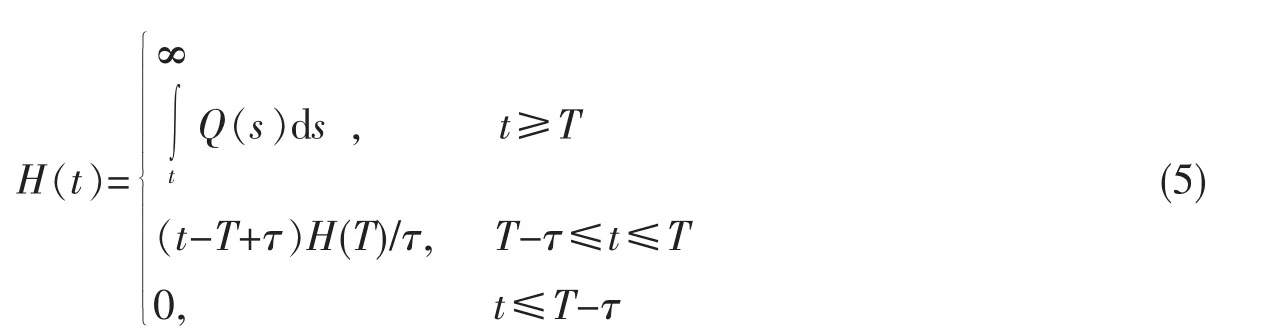
显然，H（t）是定义在R上的非负连续函数。再引入函数

可得关系式 y(t)=y(t+τ)+H（t）,t≥T。

设 t∈[T-(n+1)τ,T-nτ]，由 H（t）的性质和式(4)，

从而0≤y(t)≤1。

定义函数集合X={x∶x∈C（[T,∞),R),0≤x（t）≤y(t),t≥T}在通常偏序“≤”的意义下，(X,≤)构成一个偏序集。不难看出对于任意集合A⊂X，存在infA和supA。现在在X上定义映象S如下：

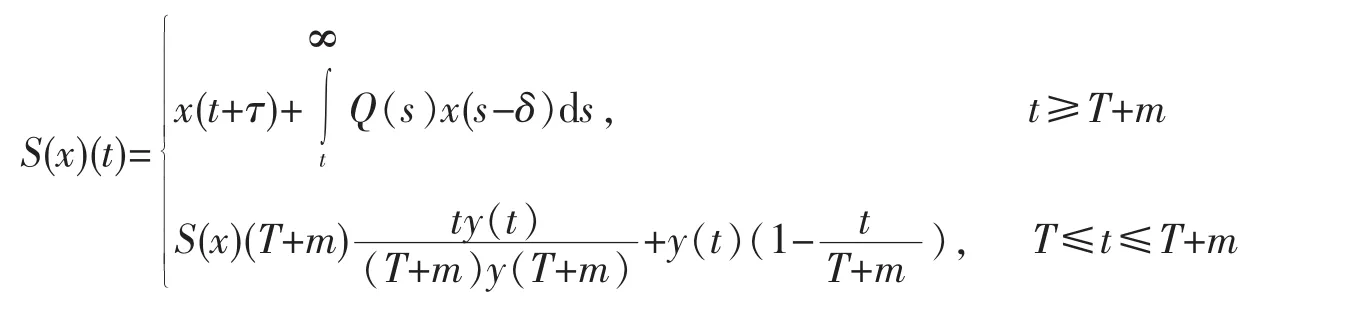
显然,当t≥T+m时，

由Knaster不动点定理，存x∈X在,使得Sx=x。这个x即方程(2)定义在上的一个连续有界正解。

充分性得证。

必要性：

假设方程(2)存在有界正解 x（t）。即 0＜α≤x（t）≤β代入方程(2)得

因而

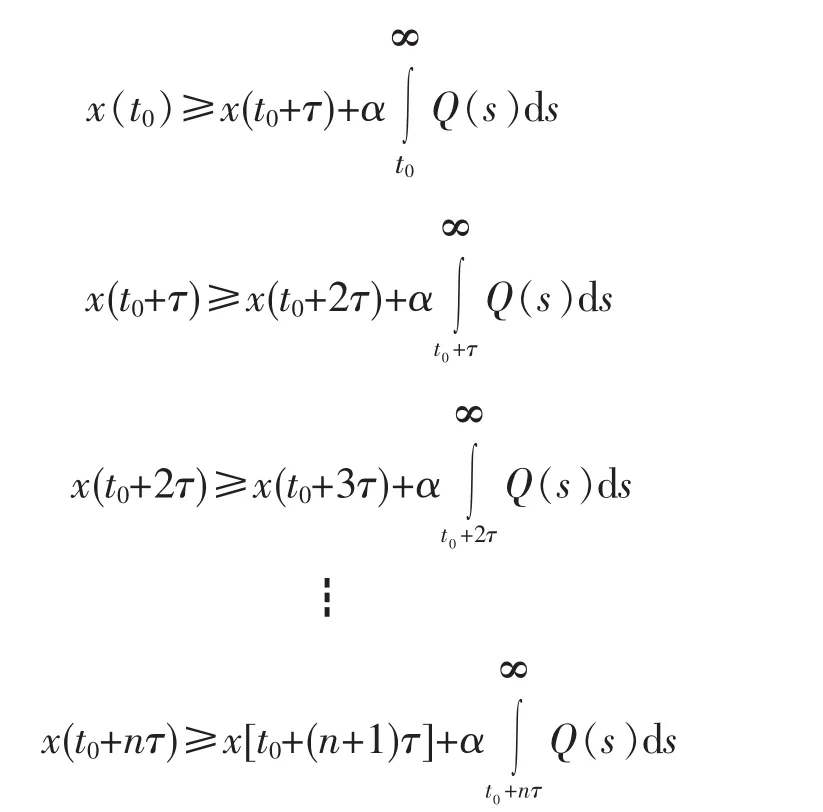
上述各式累加，得

引理 2 设 Q（t）∈C（[t0,∞),R+),τ>0，

那么(1)和(2)是等价的。

证明：(1)⇒(2)：

因为

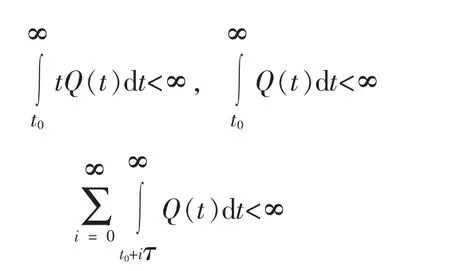
所以

(2)⇒(1)：

因为

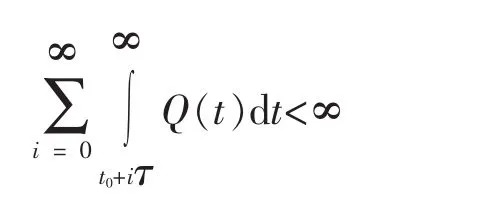
所以

从而

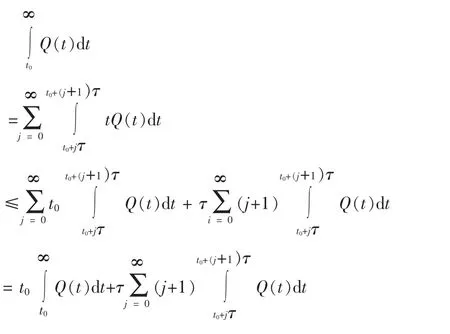
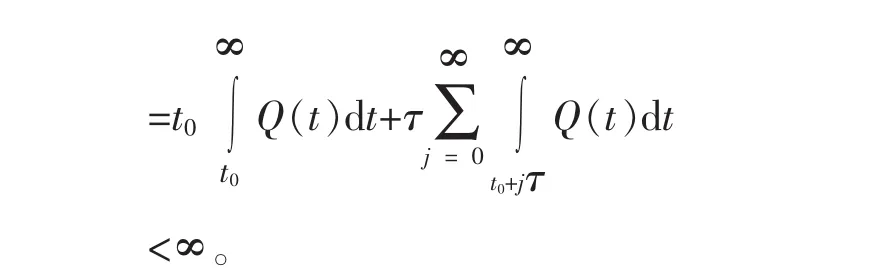
定理 方程(2)存在有界正解的充分必要条件是

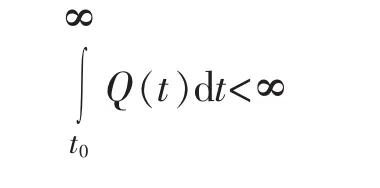
证明：

由引理1，方程(2)存在有界正解的充分必要条件是

再由引理2知

等价，所以方程(2)存在有界正解的充分必要条件是

2 意义

讨论了超前一阶中立微分方程： [x(t)-P(t)x(t-τ）]'+Q(t)x(t-δ）=0，t≥t0其中 P(t)≡1,Q(t)∈C（[t0,∞),R+,τ,δ∈(0,∞)。

得到该方程存在有界正解的充分必要条件是

这部分补充了文献[3]提出的相关问题的结论。

[1]SWANSON C A.Comparison and oscillation theory of linear differential equations[M].New York:Academic Press,1968：28-196.

[2]KRCICH K.Oscillation theory[M].New York:Springer：1973,1-98.

[3]张炳根,庾建设.关于中立型微分方程正解的存在性[J].中国科学：A辑，1992,8:785-790.