湖北省高教规模与经济水平的分析

○柳雪飞 朱 跃 侯秀梅

（武汉生物工程学院 湖北 武汉 431415）

一、引言

湖北是全国的教育大省，也是中部崛起的重要区域。湖北省高等教育发展异常迅速。为了进一步促进湖北经济和教育的健康发展，对湖北省高等教育发展与经济增长之间关系进行研究十分必要。本文的研究目的是对湖北省高等教育发展与经济增长相互作用和影响做出客观评价，为建立高等教育与经济增长相互促进的良性循环提供政策建议。

二、指标的选取与数据说明

衡量高等教育发展水平的指标主要有高校入学率、在校大学生人数、毕业大学生人数、就业人口中的大学生人数、每万人中的大学生人数等；衡量经济增长的指标主要有GDP、GNP、居民收入等。考虑到数据的可获得性和研究需要，本文选择湖北省每万人中的大学生人数（Q）和名义GDP分别作为两者的测算指标。样本数据均来自湖北统计年鉴，样本空间为1980—2013年。

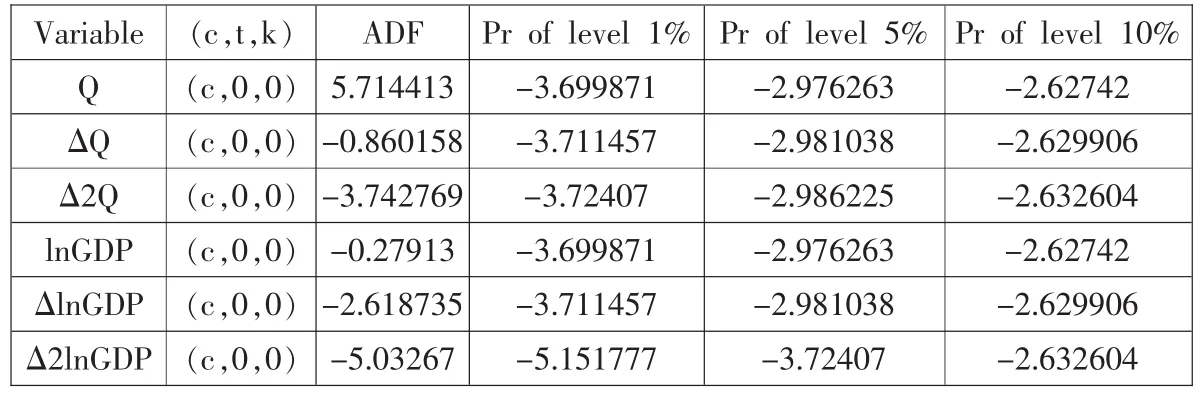
表1 Q和lnGDP的二阶差分ADF检验

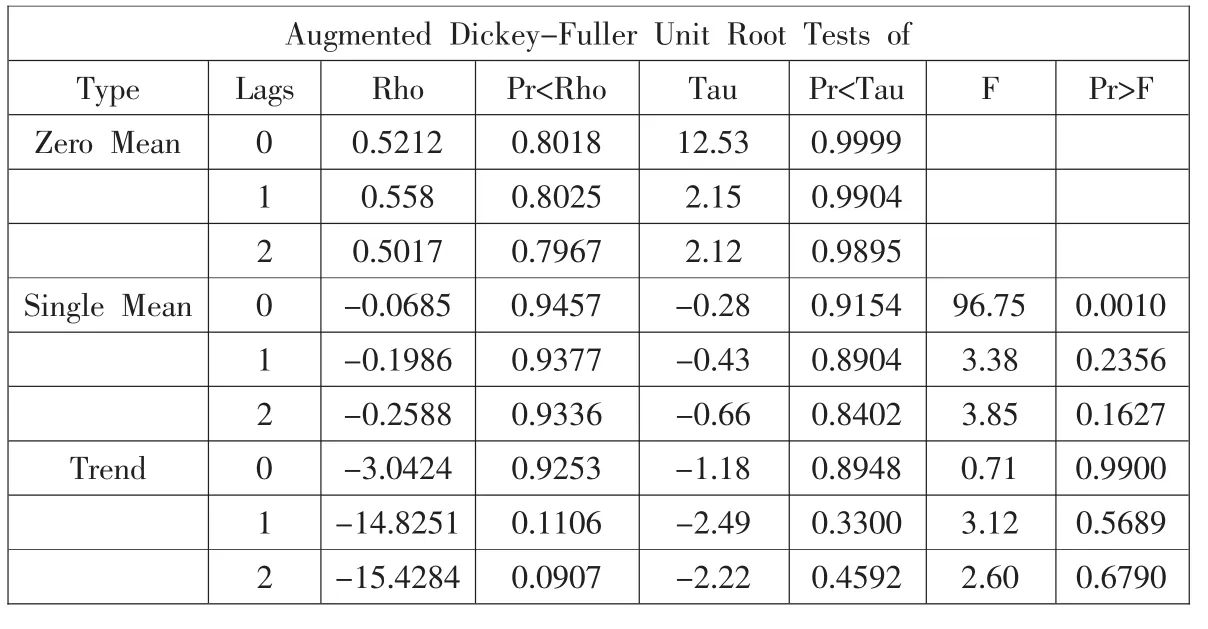
表2 残差序列的单位根检验

三、湖北高等教育发展水平与经济增长关系的协整分析

1、平稳性检验

由于对非平稳的时间序列数据建立回归模型可能会产生虚假回归问题，使得回归模型的结果变得没有解释现实的意义，因此需要进行检验以确定变量的平稳性。由于GDP数值相对Q过大，对其变量进行自然对数变换为lnGDP，不改变原序列的协整关系的同时，又能消除时间序列的异方差现象。将数据分别进行二阶差分在Eviews5.1中进行ADF检验，得到如下表1。

从上表可知，序列Q和lnGDP以及它们的一阶差分的ADF统计值均大于各显著性水平下的临界值，由此判断Q、ΔQ、lnGDP和ΔlnGDP都是非平稳的时间序列。在5%的显著性水平下，Δ2Q和Δ2lnGDP的ADF统计值小于临界值，故其二阶差分是平稳的，表明湖北地区每万人中的大学生人数Q和lnGDP变量均属于二阶单整序列，它们之间可能存在协整关系。为了证实确实存在协整关系，故我们可以对残差序列进行单位根检验，得到表2。

输出结果显示Tau统计量的P值的P值都大于显著性水平0.05，可以认为残差序列为白噪声序列，说明Δ2Q和Δ2lnGDP之间有协整关系，我们可以在这连个序列之间建立回归模型而不必担心虚假回归问题，结束分析。

2、协整关系检验

如果两个变量都是单整变量，只有当它们的单整阶相同时，才可能协整。当两个变量协整时，它们之间具有一个长期的稳定关系，可以使用经典回归模型方法建立回归模型；反之，当两个变量不是协整的，它们之间就不存在长期均衡关系，不能使用经典回归模型，否则会出现虚假回归等诸多问题。为确定湖北地区的Q和lnGDP之间是否具有协整关系，本文根据艾格（Engle）和格兰杰（Granger）提出的两步检验法（EG检验）进行协整检验。首先，采用建立半对数模型为：

从D-W值（即德宾—沃森统计量，其取值反映序列是否存在自相关）来看，该序列存在序列自相关，在SAS软件包下采用广义差分法（二阶）进行自相关处理后，估计回归模型为：

表3QR和QGDP进行ADF单位根检验

从回归估计的结果来看，模型拟合较好。可决系数和调整后的可决系数在0.9以上，表明模型在整体上拟和得非常好。截距项和斜率项的t检验值也通过5%水平下的显著性检验，表明两者的线性关系显著成立。从D-W值来看，已经消除序列相关。从长期来看，湖北省GDP的对数变动1个单位，每万人中的大学生人数就变动36.142657个。

3、误差修正模型的建立

误差修正模型（ECM）的使用是为了弥补长期静态模型的不足，建立的短期动态模型。根据格兰杰表述定理，如果变量X与Y是协整的，则它们间的短期非均衡关系总能由一个误差修正模型表述。误差修正模型既能反映不同经济序列之间的长期均衡关系，又能反映短期偏离向长期均衡修正的机制，是一种长短期结合、具有高度稳定性和可靠性的模型。前文的协整检验结果已经表明每万人中大学生人数Q与lnGDP之间具有二阶协整的关系，因此，可以建立两者的误差修正模型。其基本方法是：将长期均衡方程中各变量以一阶差分形式重新加以构造，并将长期均衡方程所产生的稳定的残差序列ut作为误差修正项引入到模型中去，并用OLS法估计出相应的参数，得到适宜的误差修正模型如下：

Q=6.1086+1.6968ΔlnGDP+0.3126ΔlnGDP+1.0369ΔQ-0.1812ut-1（3）

R2=0.854413，AdjustedR2=0.823763，F=27.87644，D-W=2.512227

其中，误差修正项ut-1=Q+292162-33185lnGDP+[AR（1）=1159，AR（2）=-0185]

误差修正模型（3）显示，误差修正项的系数为负，符合反向修正机制。模型的可决系数较高，并通过了F检验，表明整体拟和效果较好；同时也通过了D-W检验，表明模型不存在序列自相关。但是，除了变量ΔQt-1通过t检验外，其他各项均未通过，表明每万人中大学生人数Q与lnGDP之间的短期线性关系不是很显著。

四、湖北高等教育发展水平与经济增长之间的因果关系分析

前面的协整分析中已经确定了变量Q和lnGDP之间存在长期的均衡关系，但这种关系是否构成因果关系还需要进行格兰杰因果关系检验。由于格兰杰的因果性定义并没有规定变量必须是平稳的，许多学者在运用时并没有对变量进行平稳性处理。但学术界已经证实，对非平稳性变量进行格兰杰因果检验会产生问题，如虚假因果关系等。从前文的分析已知，变量Q和lnGDP均为非平稳变量，故不能直接用来做格兰杰因果检验，需做适当处理：

lnGDPRt=lnGDPt/lnGDPt-1-1，QRt=Qt/Qt-1-1 （4）

按照（4）式分别计算原序列lnGDP和Q各年（1980年除外）的环比增长率，然后再次利用Eviews5.1对变量QR和QGDP进行ADF单位根检验。从表4可知，两变量的ADF统计值都小于临界值，因此每万人中大学生人数的增长率和GDP的增长率均为平稳序列，可以进行格兰杰因果关系检验，检验结果如表3。

从分析结果可以看出，在5%的置信水平下，当滞后期数为1、4、6、7年时，每万人中大学生人数的增长率和GDP的增长率没有格兰杰因果关系；当滞后期为2、3、5年时，每万人中大学生人数Q的增长率是lnGDP的增长率的单向格兰杰原因；当滞后期为8年时，lnGDP的增长率是每万人中大学生人数Q的增长率单向格兰杰原因。

五、结论

由以上实证结果，可以得到如下几点结论。

第一，湖北省内实际经济波动是影响其教育发展水平的重要因素，教育发展对经济总量增长具有较强的依赖性，经济的增长和发展水平决定着教育发展的程度。

第二，湖北应进一步加大高等教育投入，调整结构，提高质量以更好地发挥高等教育对经济增长的促进作用根据前面有关检验及分析可以看出，湖北高等教育发展对经济增长的促进作用还不是很明显，由前面估计的协整回归方程：

可看出，实际lnGDP对每万人中大学生人数Q弹性很小，从1980年至2013年平均弹性只有约0.000349，这也从一个侧面论证了湖北高等教育发展规模对经济水平增长的贡献率很低。从定性的角度来说，高等教育对经济增长的促进作用是不言而喻的，但是实际作用的大小，还取决于高等教育的结构和质量与经济发展的适应程度，适应程度越高，促进作用越大，反之则促进作用较小。

第三，要提高湖北高等教育发展对经济增长的促进作用，还需要进一步营造良好的用人环境。湖北高校培育的人才绝大部分流向了东部沿海等经济发达地区，这相当于用自己的教育资源为其它地区培育人才。近几年来湖北在软环境建设方面已下了较大的力度，但各种优惠政策和制度改进主要是针对高层次拔尖人才，而对大量的中层次人才缺乏吸引力。但在硬环境方面还有很大不足，湖北应该根据自己的资源优势和潜力做好产业发展规划，形成有特色的产业集群凝聚效应，要大力倡导和投入科技创新，以支撑高新技术产业的领先发展，从而打下坚实的经济产业发展基础，为吸引留住大量优质人才提供肥沃的创业土壤。

（注：本文系武生院教学建模培训模式的改革与研究重点项目（2013JZ05）。）

[1]樊文汉：我国教育投资与经济增长的实证研究[J].商场现代化，2006（5）.

[2]赵修渝等：中国高等教育机会不均对个人收入差距的影响及对策研究[J].重庆大学学报（社科版），2007（2）.

[3]毛洪涛、马丹：高等教育发展与经济增长关系的计量分析[J].财经科学，2004（1）.

[4]李继怀、李拓宇：高等教育对经济发展的促进作用分析[J].教育，2004（6）.

[5]孙敬水、姚晶晶：高等教育发展与经济增长关系的协整分析[J].统计观察，2008（2）.