基于曲线相似性的负荷分类方法及其应用研究

张靠社，何优琪，刘福潮，梁雅芳

（1. 西安理工大学 水利水电学院，陕西 西安 710048；2. 甘肃省电力科学研究院，甘肃 兰州 730050）

伴随智能电网的不断发展，需求侧负荷管理技术在电网被广泛采用，负荷分类也变为电价制定、负荷预测、系统规划、负荷管理等的重要工作基础。由此，研究提出更准确有效的负荷分类方法，具有重要的理论意义和实用价值。由于电力系统综合负荷具有地域分散、类型繁多、结构复杂和非线性等特点，负荷的分类与综合已成为电力系统的一个难题[1]。现今对大量的用户负荷时序数据进行描述分析和分类控制时，在前期处理时大多数都利用的是负荷的聚类分析。

通常利用的聚类方法有模糊聚类、C—均值法、系统聚类、K—均值法、K—means聚类、基于人工神经网格和基于密度的方法[2-4]等。近年来，逐步深入的进行数据挖掘研究，涌现了许多新的聚类分析法[5-6]。文献[7]采用Ward法，该方法最终聚类数目的确定需要根据结果和经验进行选取；文献[8]采用将最大最小距离作为度量进行聚类。在负荷分类领域中，现今运用最广泛的方式是自组织映射方法（Self Organizing Mapping，SOM），文献[9]对SOM算法做了相关研究，应用中SOM方法的主要缺点是分析人员需要在计算前，提前给定分类的具体数目（K），通常需进行多次试算才能得到满意的分类结果，且很难控制负荷分类结果的精度。

针对这些负荷聚类方法算法复杂、计算量大、要求预先设定聚类初值等缺陷，为了更有效地进行负荷分类，经研究发现，一种基于曲线相似性的判定方法被广泛应用于各领域。文献[10]提出一种基于类曲率的曲线相似判定方法，并应用于图像拼接，图像修补等方向；文献[11]采用离散Fréchet 距离作为距离的测度进行研究，建立数学模型用于判定曲线相似性，利用150个随机的在线手写签名进行验证，结果匹配率高达90%以上；文献[12]对中国各个贸易大类商品中加工贸易的构成曲线进行分析归纳，得到中国加工贸易主体商品结构的演变过程。

把曲线相似性作为判定依据，应用于大规模电力负荷分类领域的研究非常少。为此，本文提出一种基于日负荷曲线，将曲线相似精度设定为分类阈值的负荷分类方法。该方法在满足事先确定的精度要求下，能将日负荷曲线集聚合成满足要求的类别。并完成某电网实测负荷样本的分类，证明该方法具有可行性和高效性，可作为系统规划、错峰管理、负荷预测的可靠依据。

1 分类方法基本理论

以下列出负荷曲线聚类方法的主要定义，含有曲线类相似精度及曲线相似度的明确概念[13]。

将n个连续观测的数据连成的曲线记为Ci=Ci（xi1，xi2，…，xin）。则可以定义Ci与Cj两条曲线间的相似度测量如下述。

定义1 曲线Ci（xi1，xi2，…，xin）和Cj（xj1，xj2，…，xjn）之间的距离：

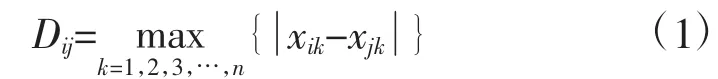
按照上面的定义1，在曲线间相应分量点距离中的最大距离就是两曲线之间的距离。距离Dij可以表征曲线的形态相似度，曲线越相似Dij值越小。只有在对应的范围内控制好曲线类中的全部曲线间的相似度，才能保证分类的结果符合一定的精度。这个“范围”即是该曲线类的“相似精度”。

定义2 记曲线类M（C1，C2，…，Cm），其中，Ci（xi1，xi2，…，xin）。曲线类M的相似精度为

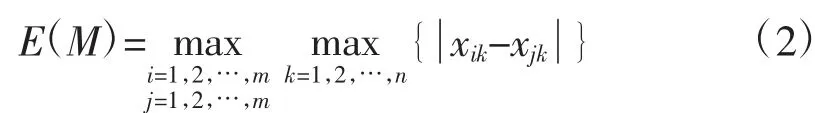
从式（2）可以看出，如果E（M）为曲线类M的相似精度是已知的，若引入一条不属于M的新曲线Ci以后变为新的曲线类M′，判定E（M′）>E（M）是否成立时，利用表达式（3）计算新曲线类M′的相似精度变得更简单。

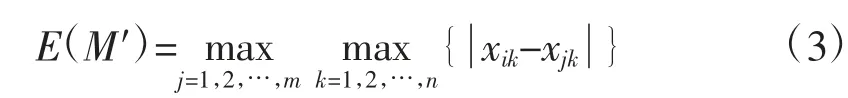
可使用以下3个定义，进一步分析曲线集合分类结果的质量。

首先给出曲线类M的质心的定义，从物理学方面来考虑，曲线类的质心就是此类曲线中各点的平均值。记M（C1，C2，…，Cm）为曲线，Ci（xi1，xi2，…，xin），1≤i≤m，定义曲线类C的质心如下表述。

定义3 曲线类M的质心为

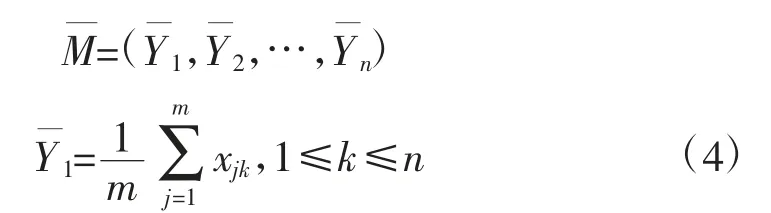
如有曲线类M（C1，C2，…，Cm），与曲线Cj（xj1，xj2，…，xjn），其中Cj不属于M，曲线Cj与曲线类M的距离同曲线Cj的平均离差定义如下表示。

定义4 定义曲线Cj和曲线类M的距离为曲线Cj与质心的距离，即

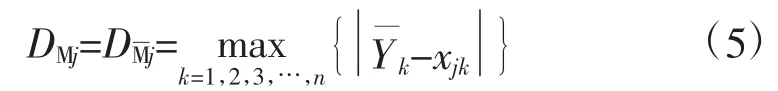
由于分类结果的优劣很大程度上会影响预测建模的精度，即使分类后得出结果，对曲线类聚集程度进行分析也是十分必要的。若曲线具有较好的分类效果，才可进行该类曲线的建模；如果曲线比较离散，某一类分类效果不佳，为保留原始信息，要求对该类曲线完成二次分类，直至得出满足要求的结果。

显示一组数据的离散程度的量化方式中，标准差是最为常用的一种。设曲线类M（C1，C2，…，Cm），其中，Cj（xj1，xj2，…，xjn），1≤j≤m其曲线类M的质心为则时刻T（1≤T≤n）该类曲线类的标准差可表示为

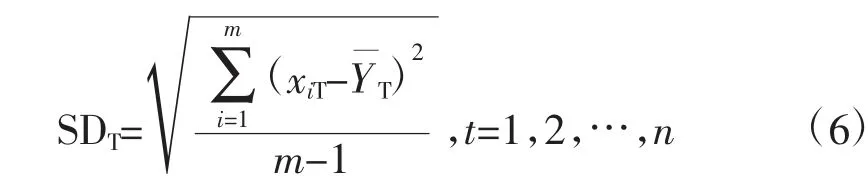
SDT体现该组数据的变异程度，其值越大变异程度就大，质心代表性越差，相反也一样。将曲线类所有时刻的标准差连起来即得该类的标准差曲线。因各类曲线的数据相差较大，因此在使用标准差曲线判定各类曲线的离散度以前，对其数据需要进行预处理。

2 负荷分类数据预处理

由于负荷数据库极大，且数据库非常容易受到不一致数据、噪声和丢失数据的影响。通常数据中存在“坏数据”或“不良数据”，为此利用数据前需先完成数据预处理，以避免其影响分类结果。本文利用的是比较滤波法[14]，该方法的原理是在T时刻，将负荷进行纵横向对比，计算出T－1时刻和T+1时刻的负荷平均值与T时刻的负荷进行比较，且计算出前一天、前两天的T时刻负荷平均值再次对比。若两个的偏差超出某一阈值，则选择横、纵向比较的平均值。

若进行系统用户负荷分类时，选取负荷特性指标的不同，很大程度影响到最后的分类结果。日负荷曲线能体现负荷随时间变化的特性，用户负荷的变化趋势和大小经日负荷曲线体现非常直观，该曲线也可以较全面反映各用户的负荷特性。在合约交易中典型日负荷曲线更是作为期货、分配电量、分析互联系统错峰效益和审核调峰能力的基础。并且利用各类型用户的用电日负荷曲线，各级电网变电站和调度中心能研究用户结构改变对用电负荷造成的重要影响，从而掌握更全面负荷的变化情况。为此，本文选择日负荷曲线作为系统负荷分类的依据。

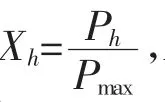
本文出现的负荷曲线都是用户日负荷曲线标准化后的结果，所以完成电力系统用户的分类工作其本质就是进行用户日负荷曲线的分类。

3 基于曲线相似精度的算法概述

下面介绍的负荷曲线分类方法是将相似精度作为阈值。此算法的基本思路为设一个曲线集合为M。按照具体需求，开始选定一个相似精度，并且把其作为分类时使用的终止阈值，然后选择M中间曲线距离最大的两条。将任一条定成聚核开始聚类，若出现此类相似精度达到阈值的情况，则停止聚类，从而聚类出首个曲线类M1。定M2=M－M1，由此曲线集合M2完成相同聚类步骤，在全部曲线均归到特定类别后，算法停止。此算法的具体步骤如下：

针对给定曲线集M（C1，C2，…，Cm），设W作为曲线聚类的相似精度阈值。1）在曲线集合M中计算两两曲线间的距离，挑选出两两间距离最大的一条曲线，记为A；2）将A归到曲线类M1，中，并记M=MM1；3）曲线集合M中，将集合M1同各曲线的距离计算出来，得最小距离相应的曲线B，并记M1′=M1+B；4）按照式（3）计算E（M1′）。如果E（M1′）>W，那么算法转至1）。反之把B归到曲线类M1中，分别记M1=M1+B；M=M－M1，算法转3）；5）若M是空集，那么有算法停止。

根据所取得的聚类结果，可以再综合每一条曲线Cj，j=1，2，…，m，至曲线类质心M軓的距离，以及各条曲线Cj，j=1，2，…，m的离差平均值。从整体全面地把握任一曲线的归类精度和分类效果的分布状况。

4 应用实例分析

本文从某电网选取370个用户负荷的时序数据，同时采用模糊C均值聚类（Fuzzy C-Means，FCM）方法与负荷曲线分类方法对该电网的用户负荷分别进行分类。首先利用FCM方法对370条日负荷曲线进行分类，在划分的聚类算法理论基础之上，FCM方法的思想是保证被归到同一类的对象间的相似度最大，非同类之间的相似度最小。首先需要确定聚类数目并建立模糊相似矩阵，才能开始迭代直至目标函数收敛到最小值，最后显示聚类结果。利用距离聚类方法对样本数据进行分类，得最优分类数是十类，分析得到的这十类负荷曲线的簇集程度。计算出每一类各时刻的标准差，绘制各类负荷的标准差曲线如图1示，由图1可表明标准差曲线中第一类、第七类与第九类明显高于其他负荷曲线，显示这些类曲线簇中的负荷曲线分布较为分散。为此，需进行再次分类的为此三类负荷曲线，以确保对用户负荷曲线初始信息的准确辨识。

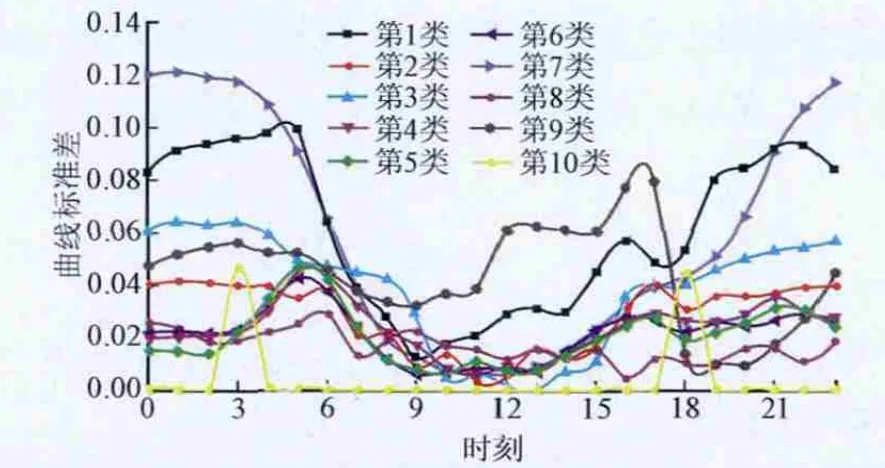
图1 十类标准差曲线Fig. 1 Ten class standard deviation curves

依照标准差结果图，其中有三个曲线类（第一类、第七类与第九类）的聚集不够理想，分类以后效果较差，且其负荷的均值曲线代表性较差，用此直接进行辨识或预测，导致误差很大。分类效果较好的是七类，控制标准差都在0.7之下，需对聚集效果不理想的三类中的曲线进行二次分类，以确保每一类的精度。第一类曲线含有38条，第七类曲线包含98条，第九类曲线包含44条，依次对其完成二次分类，总共分为六类，再对二次分类的六类曲线进行簇集度分析，求其六类的标准差及标准差曲线，如图2所示。

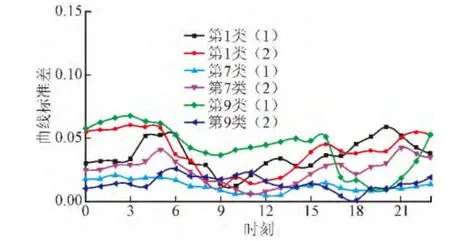
图2 二次分类后六类标准差曲线Fig. 2 Six standard deviation curves after secondary classification

图2中表明对第一类、第七类和第九类二次分类，得到较好的分类结果，明显改善了各类中的曲线类聚集程度。最终把用户的370条日负荷曲线分成十三大类，同时将每条曲线的标准差控制在0.07以下，分类效果良好。通过上述分类过程看出，FCM方法是应用较为广泛聚类方法，能顺利完成大规模曲线的分类，并具有较好的分类效果。但因FCM聚类需要预先指定分类数目，需要进行聚类的有效性检验，所以其具有分类效率和准确性低的缺点。

鉴于此，以下使用本文中基于曲线相似性的负荷分类方法进行该电网的负荷分类。因分类依据是在日负荷曲线的原始形状基础上，且各负荷具有量纲不一致的难题，但预先已对370个用户负荷的时序数据进行标准化处理，再利用新的负荷曲线分类方法进行分类，设定0.5为所选日曲线类相似精度的阈值。该方法把370条不同用户曲线聚类成十三类，所得到每类的最大值、最小值以及均值曲线，如图3所示。

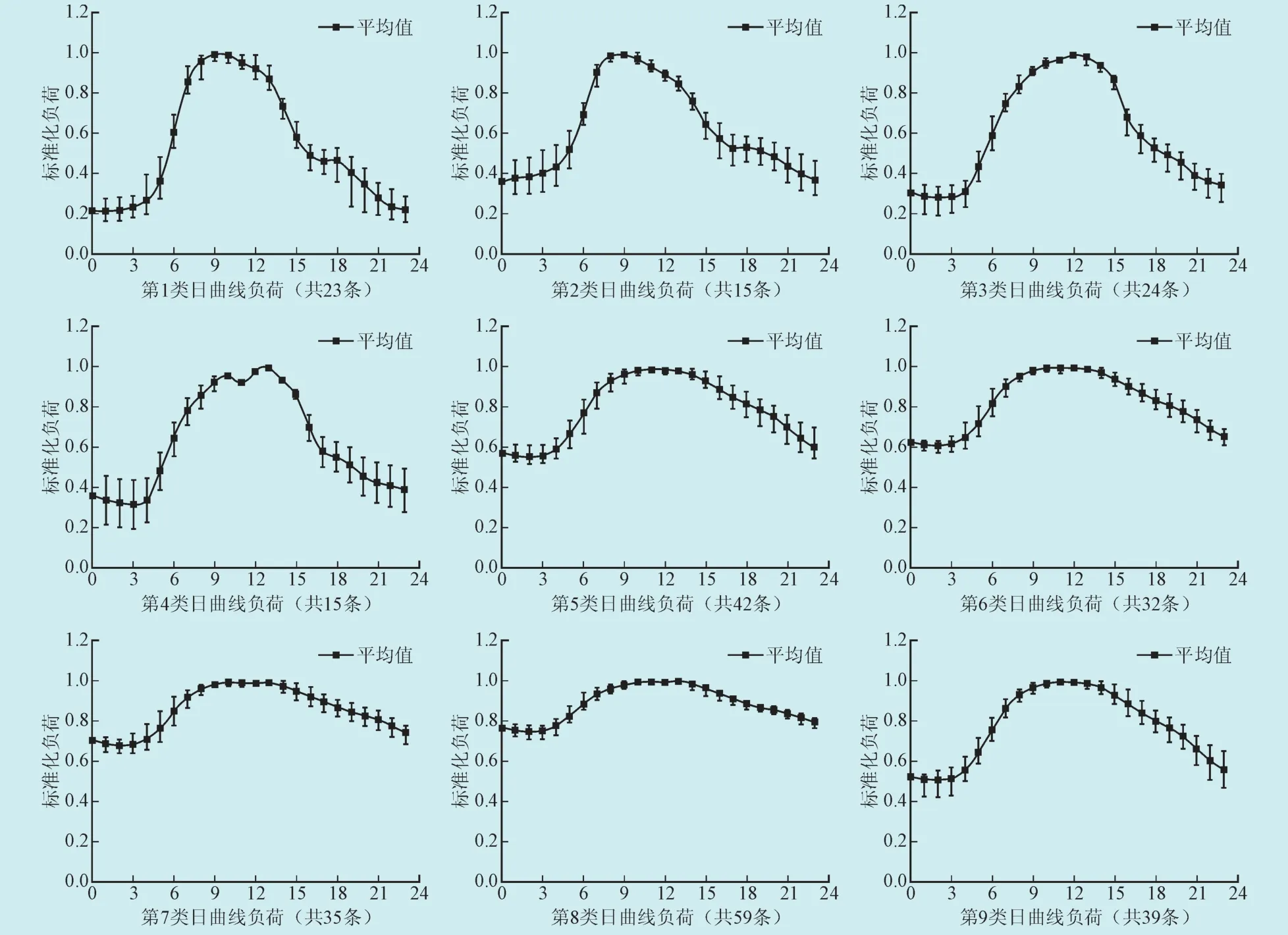
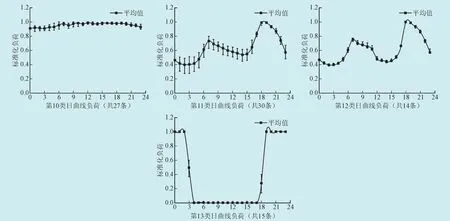
图3 基于曲线相似性分类算法效果图Fig. 3 Classification algorithm renderings based on the similarity of curves

依照图3可知，其中每一类的分类效果良好。效果图显示，采用新的负荷曲线分类法所得的结果，同使用模糊C均值聚类法的分类结果相差并不大，优点在于很大程度上减少了分类的工作量，实现了更准确有效进行负荷分类的目标。计算求出各类曲线的标准差，效果图4中得，若把每一类标准差均控制在0.7以下，分类产生良好效果，且曲线簇集程度较好。

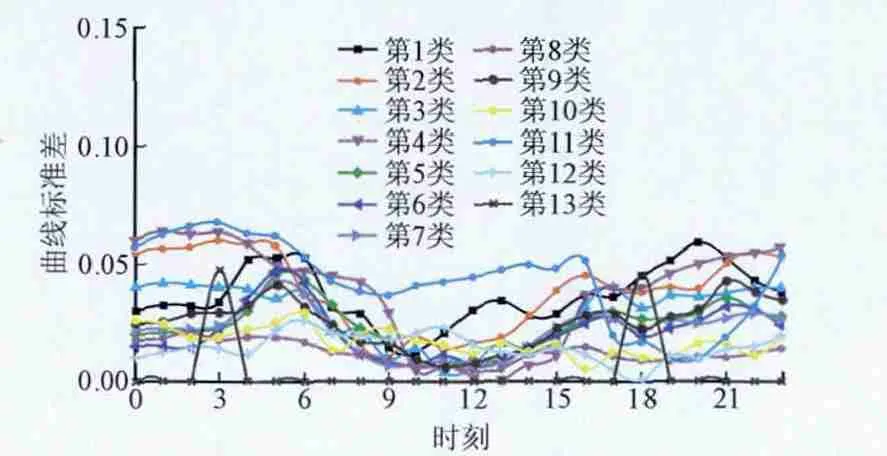
图4 十三类标准差曲线Fig. 4 Thirteen class standard deviation curve

将上述计算出的每一类负荷曲线的算术均值，当成此类用户的典型日负荷曲线，其对电网的运行、规划和负荷管理都具有重要意义，同时在电力市场条件下，更是作为期货、合约交易中分配电量，审核调峰能力及分析互联系统错峰效益的基础。

5 结语

本文提出了一种基于曲线相似性的负荷分类方法，依照相似精度的阈值将日负荷曲线集地划分成若干的曲线类别，其结果可做为系统规划、负荷管理和控制的依据。通过实例分析，该方法可以高效地得出满足相似精度要求的分类结果，能大幅度降低系统负荷管理的难度与复杂度。

[1] 林舜江，李欣然，刘杨华，等. 电力负荷动特性分类方法研究[J]. 电力系统自动化，2005，29（22）: 33-38.LIN Shunjiang，LI Xinran，LIU Yanghua，et al. A classification method for aggregated load dynamic characteristics[J]. Automation of Electric Power Systems，2005，29（22）: 33-38（in Chinese）.

[2] TSEKOURAS G J，KOTOULAS P B，TSIREKIS C D. A pattern recognition methodology for evaluation of load profiles and typical days of large electricity customers[J].Electric Power Systems Research，2008（27）: 1494-1510.

[3] BIDOKI S M，MAHMOUDI-KOHAN N. Evaluating different clustering techniques for electricity customer classification[C]. Transmission and Distribution Conference and Exposition，2010 IEEE PES: 1-5.

[4] Teemu rasanen，Dimitrios Voukantsis. Data-based method for creating electricity use load profiles using large amount of customer-specific hourly measured electricity use data[J].Applied Energy，2010（87）: 3538-3545.

[5] WANG Wensheng，WANG Jin，WANG Kewen. Application of SOM neural network and C-means method in load classification[J]. Proceedings of the CSU-EPSA，2011，23（4）: 36-39.

[6] 周欢，李广明，张高煜. SOM+K-means两阶段聚类算法及其应用[J]. 计算机应用技术，2010（16）: 113-116.ZHOU Huan，LI Guangming，ZHANG Gaoyu. SOM+Kmeans two-phase clustering algorithm and its application[J].Modern Electronics Technique，2010（16）: 113-116（in Chinese）.

[7] TANG Guangze，WANG Jin，LI Cailing. Study on characteristics classification of power load based on ward method[J]. Journal of Electric Power，2008，12（23）: 470-473.

[8] 周涓，熊忠阳，张玉芳，等. 基于最大最小距离法的多中心聚类算法[J]. 计算机用，2006，26（6）: 1425-1428.ZHOU Juan，XIONG Zhongyang，ZHANG Yufang，et al.Multiseed clustering algorithm based on max-min distance means[J]. Computer Applications，2006，26（6）: 1425-1428（in Chinese）.

[9] YU Jian，GUO Ping. Research of clustering algorithm of self-organizing maps neural networks[J]. Modern Computer，2007（255）: 7-9.

[10] 于昊，赵乃良，陈小雕. 类曲率在曲线相似性判定中的应用[J]. 中国图象图形学报，2012，17（5）: 707-714.YU Hao，ZHAO Nailiang，CHEN Xiaodiao.Quasi-curvature and its application in similarity measurement of curves[J].Journal of Image and Graphics，2012，17（5）: 707-714（in Chinese）.

[11] 朱洁，黄樟灿，彭晓琳. 基于离散Fréchet 距离的判别曲线相似性的算法[J]. 武汉大学学报：理学版，2009，55（2）: 227-232.ZHU Jie，HUANG Zhangcan，PENG Xiaolin. Curve similarity judgment based on the discrete fréchet distance[J].Wuhan University Journal，2009，55（2）: 227-232（in Chinese）.

[12] 叶明. 中国加工贸易商品演变过程分析—基于曲线聚类方法研究[J]. 世界经济研究，2011（8）: 49-54.YE Ming. The evolution of China’s processing trade goods:an analysis based on the curves clustering method[J]. World Economy Study，2011（8）: 49-54（in Chinese）.

[13] 叶明，王惠文，寇微. 大规模曲线的自动分类方法及其应用[J]. 系统管理学报，2010，19（2）: 640-644.YE Ming. WANG Huiwen，KOU Wei. Automatic classification method of large-scale curves and application[J].Journal of Systems＆Management，2010，19（2）: 640-644（in Chinese）.

[14] 冯晓蒲.基于实际负荷曲线的电力用户分类技术研究[D].北京: 华北电力大学，2010.

[15] 鞠平，金艳，吴峰，等. 综合负荷特性的分类综合方法及其应用[J]. 电力系统自动化，2004，28（1）: 64-68.JU Ping，JIN Yan，WU Feng，et al. Studieson classifieation and synthesis of cornposite dynarnie loads[J]. Automation of Eleetrie Power Systems，2004，28（1）: 64-68（in Chinese）.

[16] 张忠华. 电力系统负荷分类研究[D]. 天津: 天津大学，2007.

[17] 贺仁睦，刘应梅. 基于KOHONEN神经网络的电力系统负荷动特性聚类与综合[J]. 中国电机工程学报，2003，23（5）: 1-5.HE Renmu，LIU Yingmei. The characteristics clustering and synthesis of electric dynamic loads based on KOHONEN neural network[J]. Proceedings of the CSEE，2003，23（5）:1-5（in Chinese）.