浮标LOFIX定位时目标轨迹的AR滤波

刘桂瑜 乔斌 张磊 凌震莹

（第七一五研究所，杭州，310023）

被动全向声呐浮标具有隐蔽性强、工作距离远、效费比高、方便携带等优点，是航空反潜最常用的一种探测器材。距离比定位（LOFIX）利用多枚浮标收到的目标辐射强度，得出距离圆定位，是被动全向声呐定位的主要方法。LOFIX的定位误差在0.5～1 n mile，一般用作对目标的初始定位。距离圆的交点即为可能目标位置解，然后利用位置解到各浮标距离和最小的准则可以判断真实目标解，但是此方法并不总是有效。本文研究了在欠浮标（三枚）情况下两个距离圆的交点时，如何利用AR预测滤波估算目标解。

1 定位方法及原理分析

假设目标声源为点声源，其辐射方向性、浮标接收水听器方向性及传输介质是各向均匀的，忽略低频吸收因素影响，根据两个浮标接收到的同一个线谱的幅度比计算距离比，就可以确定一个目标距离圆轨迹，此圆的圆心位于两枚浮标位置的连线上并靠近接收信号大的浮标一侧。如果同时有三枚浮标收到同一个线谱，就可以得到两个圆，得到两个可能的目标位置解[1-4]。

设浮标位置为 B1(xB1,yB1)、B2(xB2,yB2)、B3(xB3,yB3)，目标实际位置为 T(xT,yT)，距离圆的圆心为 C1(xC1,yC1)、C2(xC2,yC2)，相应的浮标间距在直角坐标系下为d12、d13、d23，两枚浮标确定的距离圆半径为R12、R13。

目标距离比：

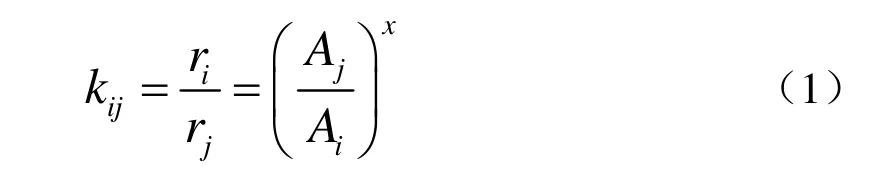
其中Aj、Ai是两枚浮标收到信号频域的幅度值，x是一个与声波传播几何衰减有关的值。

距离圆圆心为：

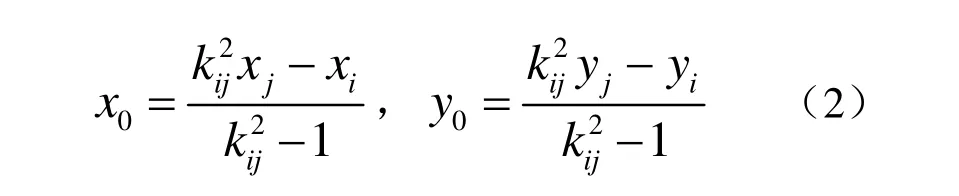
距离圆半径：

实际情况下一般同时使用至少四枚浮标进行定位，多个距离圆相交产生多个可能的目标解，式（4）对应的目标序号 j即为所要求的目标解：

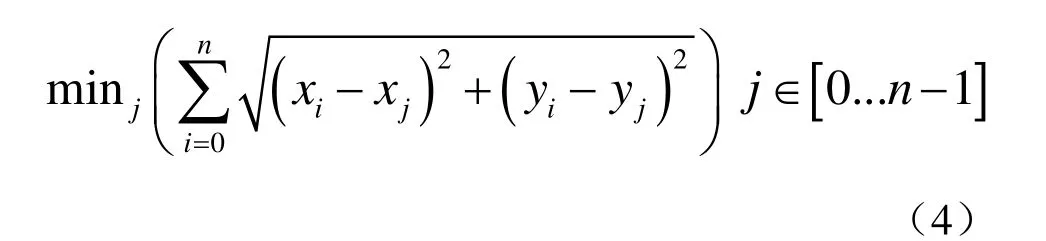
LOFIX定位的解算原理如图1所示。

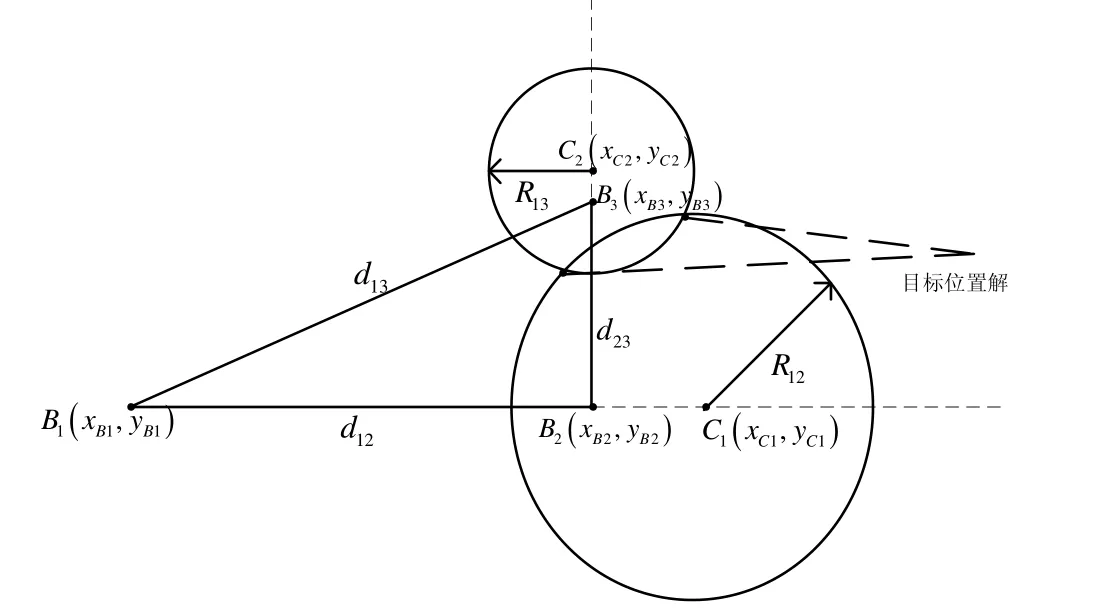
图1 LOFIX距离圆定位示意图

2 AR预测滤波在欠浮标情况下的应用

2.1 AR滤波简介

假设x是一个AR(p)过程，在以前p个数据样本的基础上预测，即：

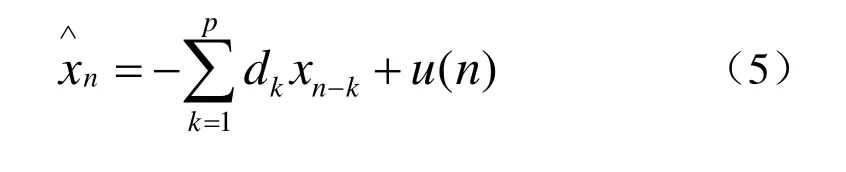
其中dk为AR模型的预测参数，u(n)是方差为σ2的激励白噪声，数据样本x(n)的自相关函数为：

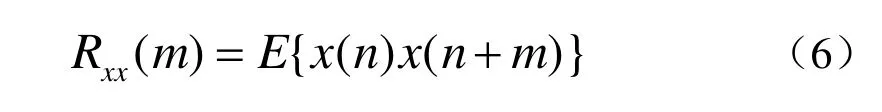
将式（5）代入并化简可得Yule-Walker方程：

写成矩阵方程形式[5]：

通过解矩阵方程，求出滤波器的系数{d1, d2,...,dp}，使预测功率Qp最小，进而求得预测值。一般来说，AR模型的阶数并不是先验已知的，为了避免AR模型的失配引起的预测误差过大，要求 k≤N /2，其中 N为记录数据的样本个数。

2.2 欠浮标情况下位置解

由第1节分析可知，三枚浮标会产生两个可能的交点目标解S1、S2，真正的目标解记S，由式（4）利用位置解到浮标距离和最小的准则可以判定真实目标解，但是目标一旦超出浮标所围成的几何区域外，此方法很可能会失效。

浮标探测的目标速度一般较慢（相对定位时间），运动轨迹不会产生剧烈的突变，相邻的若干运动轨迹点之间有较强的相关性，可以考虑使用AR预测滤波作为判定目标解的一种准则。假设在N时刻之前有p点目标解xn−k，k=1…p，由2.1节可知使用该预测样本建立AR预测滤波器得出N时刻的目标解预测值SAR，然后求取S1、S2与预测值SAR之间的距离：

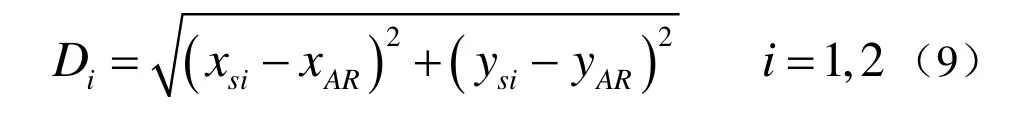
由上述分析可知，由AR预测得出的N时刻的预测值SAR与样本的位置信息有较强的相关性，则可认为距离较小的交点目标解是真正的目标解 S。然后把目标解 S作为一个最新的样本数据加入xn−k，即xn−1=S，xn−p舍弃，作为N+1时刻的预测样本，同理可以解算出N+1的真实目标解，以此类推，求解N+k时刻的真实目标解。

3 仿真及性能分析

3.1 仿真环境条件

● 目标声源到各枚浮标的声波传播速度相同；

● 3枚浮标的坐标为B1(0,0)、B2（0,3.33）、B3(3,5)，单位均为km（下同），目标均在各浮标的作用范围内；

● 目标产生1000 Hz单频信号，信噪比为70 dB，信号随距离的20lg10(r)衰减，声波衰减指数为2；目标的运动轨迹为T(0.46, 0.72)到T(1,2)；

● 两个距离圆的交点分别为S1(x1, y1)，S2(x2,y2)，真正的目标解记为S(x,y)；

● 每次的样本数据使用 11个目标位置数据，且AR滤波器的阶数为4。

3.2 仿真

图2为两个距离圆相交于两个交点，其中右侧交点为真正的目标解；图3为三枚浮标对运动的目标连续 LOFIX定位，并使用本文的算法解算目标解，可见解算的目标解均正确。AR模型和线性预测器是等价的[6]，是在最小平方意义上对数据的拟合，在满足一定信噪比的情况下，AR模型具有较好的性能。AR模型阶次的选择一般使用两个较常用的准则：最终预测误差准则，信息论准则。实际上对一个AR模型阶次的选择需要对所使用的具体信号得到的结果多次比较确定。可以根据数据的规律，从低次到高次不断的实验，当最后一项系数为0或者很小时，就可以停止了。

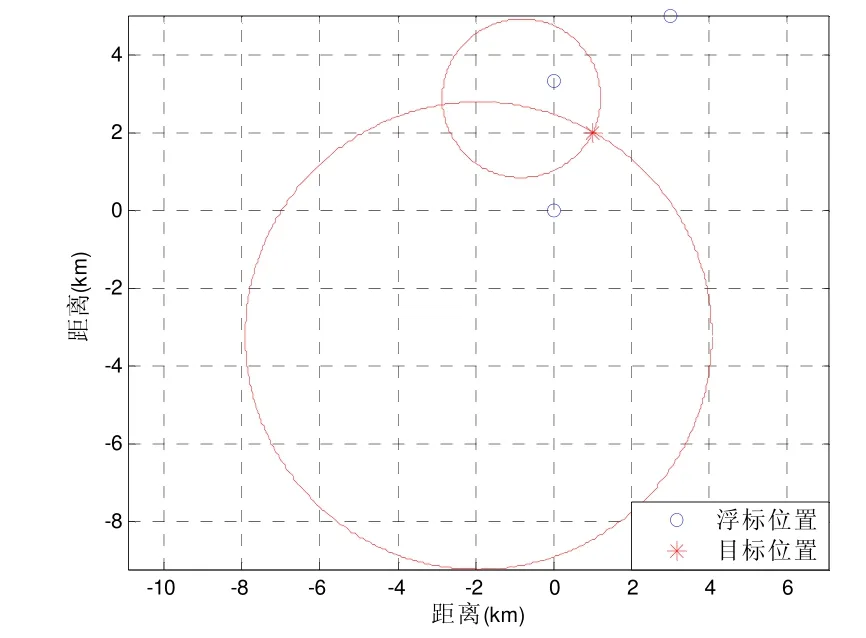
图2 距离圆示意图

图3 目标位置解

由仿真结果可知使用本文方法可以较好的解算目标位置解，目标位置变化较为平缓，4阶 AR时最后一项的系数已经很小，故使用4阶已经合适。但是同时也可以看出，本文使用的模型较为理想，实际上海洋环境具有高度的复杂性和不确定性，LOFIX定位的误差受诸多因素影响，当LOFIX定位误差较大时，本文算法使用样本数据已经不准确，可能会影响目标解算点。

4 结束语

LOFIX作为被动全向浮标的一种主要的定位方法，具有造价低、经济性好的优点，多在搜潜的初始阶段使用。多数情况下，还需要使用被动定向或主动全向浮标做进一步的精确定位。在欠浮标情况下，两个距离圆只有两个可能目标交点，本文使用AR预测滤波来判定真正的目标解，在一定程度上为扩大被动全向浮标的使用范围提供了一些思路，对实际的工程应用也有一定得借鉴意义。实际情况下一般使用多于四枚浮标进行 LOFIX定位，得到的目标位置解较多，为一定的概率区域，可考虑使用AR模型对每一个位置解做进一步的轨迹滤波，剔除一些误差较大的位置解，进一步缩小位置解概率区域，提高定位的精度与稳定性，这也是作者下一步的研究方向。

[1]孙明太. 航空反潜战术[M]. 北京: 军事科学出版社,2003.

[2]赵绪明. 航空搜潜战术模型与仿真研究[D]. 烟台: 海军航空工程学院, 2005.

[3]杨福渠, 鄂群, 刘德才. 被动声呐浮标距离比定位[J].声学与电子工程, 2000,(3):28-32.

[4]孙辉,李建辉,胡柱喜. 被动全向浮标 LOFIX定位精度仿真分析[J]. 声学与电子工程, 2009,(3):14-17.

[5]肖国有, 屠庆平. 声信号处理及应用[M]. 西安: 西北工业大学出版社, 1994.

[6]胡广书. 数字信号处理[M]. 北京: 清华大学出版社,2003.