基于改进的BP神经网络的大坝蓄水期实时预报模型

夏天倚 刘天祥 钟黎雨 陶 亮

（1.河海大学 水文水资源与水利工程科学国家重点实验室，南京 210098；2.河海大学 水资源高效利用与工程安全国家工程研究中心，南京 210098；3.河海大学 水利水电学院，南京 210098）

大坝原型监测在保证坝工安全上具有至关重要的作用.安全监测可以监视水工建筑物在初次蓄水期间以及随后长期运行工作的安全，并在施工过程中不断反馈，提高设计和施工水平［1］.目前，大坝安全监测资料分析模型主要有统计模型［2］，人工神经网络模型［3］，灰色模型［4］等单一分析模型以及多个子模型［5］组合而成的综合分析模型.神经网络由于兼具高度容错性、鲁棒性以及大规模并行处理特征［6］，被广泛应用在非线性系统的研究领域，因而特别适用于大坝监测预报研究.大坝时效位移的变化规律一定程度上反应了大坝的工作性态.时效位移突然增大或变化急剧变化即为大坝或地基病态工作的预兆［7］.而时效位移具有在初次蓄水时期剧烈变化的特点.在处理波动性较大、平稳性不足的蓄水期资料时，传统的BP神经网络模型往往预测精度不够理想.同时，由于初期蓄水时期水位的分期升高，坝体的整体性态也会有所变化，早期的观测资料并不适用于近期的拟合和预测，具有时变性和阶段性［8］.因而需要建立动态的监测模型.在传统的BP神经网络的基础上引入遗忘因子，以实现对观测资料的实时更新处理，特别针对初期蓄水情况下，分期抬高水位并保持平稳的变化特征，建立遗忘矩阵，减弱早期数据对预测结果的影响，实现对大坝监测资料分析预测的动态调整.

1 传统的BP神经网络

作为训练人工神经网络的基本方法，误差反向传播算法人工神经网络即BP神经网络（Back Propagation Algorithm of Artificial Neural Networks）由输入层（Input layer）、一个或多个隐含层（Hidden layer）和一个输出层（Output layer）3大部分组成.工作结构主要包括输入的影响因子数据资料在网络内的正向传播和反馈的计算误差的自后向前的反馈传播两个工作过程.其拓扑结构形式如图1所示.

图1 BP神经网络拓扑图

所谓正向传播阶段，包括信息处理、误差计算、信息传递3个部分.数据在层际神经元之间传递即为信息传递.而相互关系通过附加传递权值W 确定.信息处理即为信号经过激发函数，输出计算结果.误差计算指输出层神经元输出值与目标值的误差计算.当误差超出容许值时，连接向量W 按照梯度向下法进行修正计算；将计算值沿着正向信息传递的逆向，将W传递；因而将这一过程称为反向计算过程.当误差在容许值范围内时，退出计算.而这需要经过不断重复的迭代计算.

假设整个网络的输出为y.输入层、输出层分别含有n、m 个神经元.假设xj（j＝1，2，3，…，p）为某神经元输入，则隐层各神经元的输出分别为

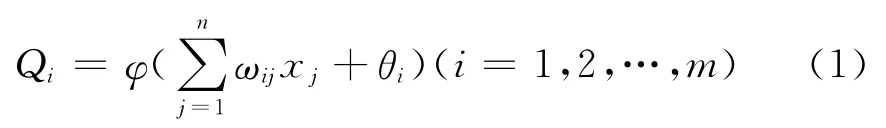
式中，ωij为隐含层神经元i与输入层神经元j的连接权重；θi为隐含层神经元的阈值；φ（x）为激发函数.整个网络的输出

式中，vi是输出层神经元与隐含层神经元i的连接权值.

以上为网络的正向计算过程.对某一学习样本xj（j＝1，2，…，p），当网络向量W（通常可以事先设定初始运算W）已经设定后，可以通过公式（1）和（2）正向计算出输出值Y（n），对应目标学习样本实测值G（n），其在第j个神经元上的误差信号为

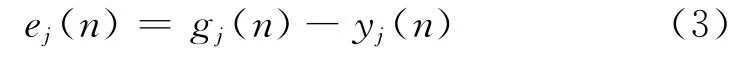
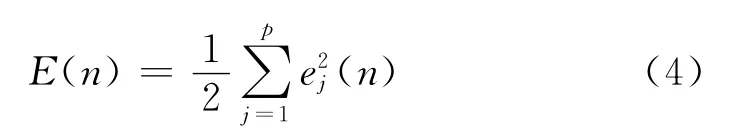
则对于整个计算过程，计算训练误差平方和.设用于训练的学习样本数量为N，则

则训练的目标就是通过与目标样本的不断比较求得一组权值W，使得EG得到最小值［9］

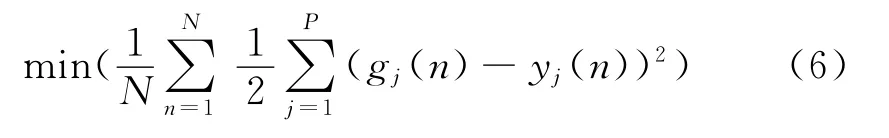
2 改进的BP神经网络模型原理

考虑到初次蓄水期，水位分段抬高、保持平稳、再次抬高的变化特点，距离预测点时间越近的数据，代表规律越为明显，越能为以后的预测提供有价值的信息.本文对应蓄水初期实测资料，对应不同的时间数据赋予不同的权值，较近的时间序列所赋权值较重，较远的时间时间序列所赋权值较轻，经过神经网络的训练后，得到考虑前期作用且能重点体现近期变化特点的权值W应用于预测.

对某一学习样本xj（j＝1，2，…，p），经过公式（1）和（2）可得到，相应于第j个神经元，其相对于实测值的误差信号为

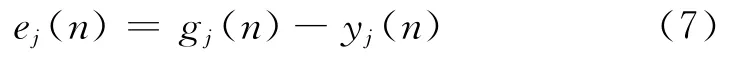
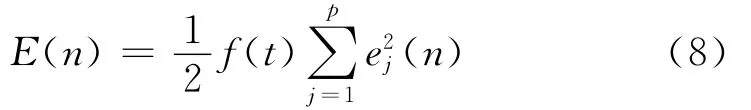
对应式（4），通过对应学习目标样本对网络的迭代训练，不断修正传播权值，最终得到一组权值W，使得目标函数EG取最小值，即

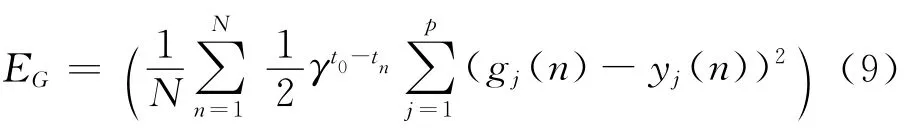
3 改进的BP神经网络模型算法

引入遗忘函数的BP神经网络具体算法步骤：

步骤1：网络初始化.考虑到数据不同系列之间差异较大，将输入数据按照（－1，1）的均匀分布.随机对输入数据赋初值Wij（0）.

步骤2：输入样本.输入样本xj（j＝1，2，…，p），gj（n）为第n个样本的期望输出.

其中，ωji为i层到j层的连接权值.

步骤4：引入遗忘因子，计算预测值与实测值误差平方和EG

步骤5：反向权值修正δ.

1）反向计算

对于输出单元

对于隐层单元

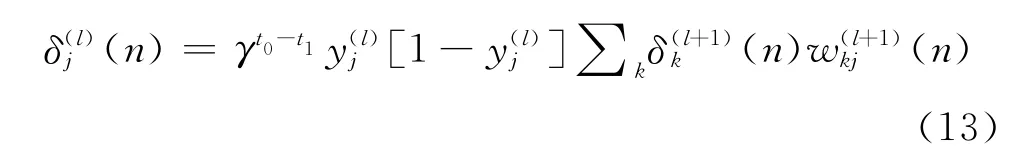
2）自输出层向输入层自后向前修正连接权

式中，η为学习率.

步骤6：n＝n＋1转至步骤2.运算直至误差平方和EG达到预定要求或者训练次数达到预定上限即可退出运算.

4 实例分析

取某混凝土高拱坝1 778高程处某点位移监测点径向位移进行资料分析，图2为初次蓄水期上游水位变化过程线，可见水位变化大致分为两个阶梯式阶段.第1阶段蓄水结束后，水位保持较长时间平稳状态直至2013年6月15日开始第2阶段蓄水，库水位开始上升，2013年6月29日停止蓄水，库水位短暂维持平稳后继续蓄水，2013年7月19日停止蓄水，之后维持该水位.为验证该方法对于变化较大的数据的处理能力，选取第2阶段蓄水期2013年6月10日至2013年10月13日126d数据作为分析时间序列.

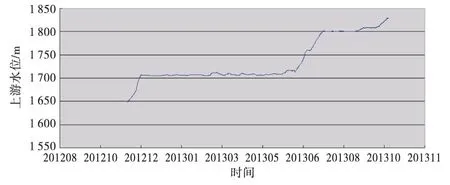
图2 蓄水期上游水位变化过程线

4.1 因子选择

坝体位移主要考虑水压、温度以及时效等因子对其产生的影响，本文选取水压分量δH、温度分量δT和时效分量δθ（趋势性分量）对坝体1 778高程处某一点的径向位移进行相关性分析.即δ（x，y，z）＝δH＋δT＋δθ.

水压因子选取：δH与水头H 的幂次方呈比例关系，故取 H1，H2，H3，H4，H55个因子.

温度因子选取：当混凝土水化热已散发，坝体内部温度达到稳定温度场，此时仅取决于边界温度变化，一般水温和气温作简谐变化，则混凝土内部的温度也作简谐变化.因此，选用多周期的简谐波作为因子［1］.即

时效因子选取：在蓄水初期δθ与θ成非线性.通常为对数、指数函数或双曲线等.对于坝体某一固定点的时效分量，可用下式表示：

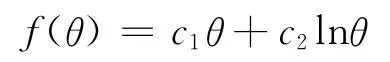
故取时效因子θ、lnθ，其中θ为测值当日到起测日的累计天数除以100［10］.共计有9个输入层因子.根据经验公式可知，隐含层节点数取（2n＋1）［11］个＝19个节点.以sigmoid函数为激发函数.

4.2 实验结果及分析

选择20130610～20131013共126d数据作为分析资料，选择前108个数据作为训练样本，后18个样本作为测试样本以检验所建立模型的正确性，通过自编程序实现拟合与预测.先后对比使用传统的BP神经网络算法模型预测的成果和使用改进后的BP神经网络算法模型计算的结果，通过对108个数据进行反复训练对比后，选择效果最好的W 预测20130926至20131013，共计18个样本.在应用改进后的BP神经网络时，添加遗忘矩阵，经过反复试算对比，取γ＝0.923 3时效果最好，学习速率取0.01，网络误差取0.01，计算次数31 487次.将预测输出与实际测量结果相比较，为了使计算结果更加明显，根据式（16）计算出预测输出与实测值的绝对误差，根据式（17）计算出相对误差，预测结果与实测结果见表1.

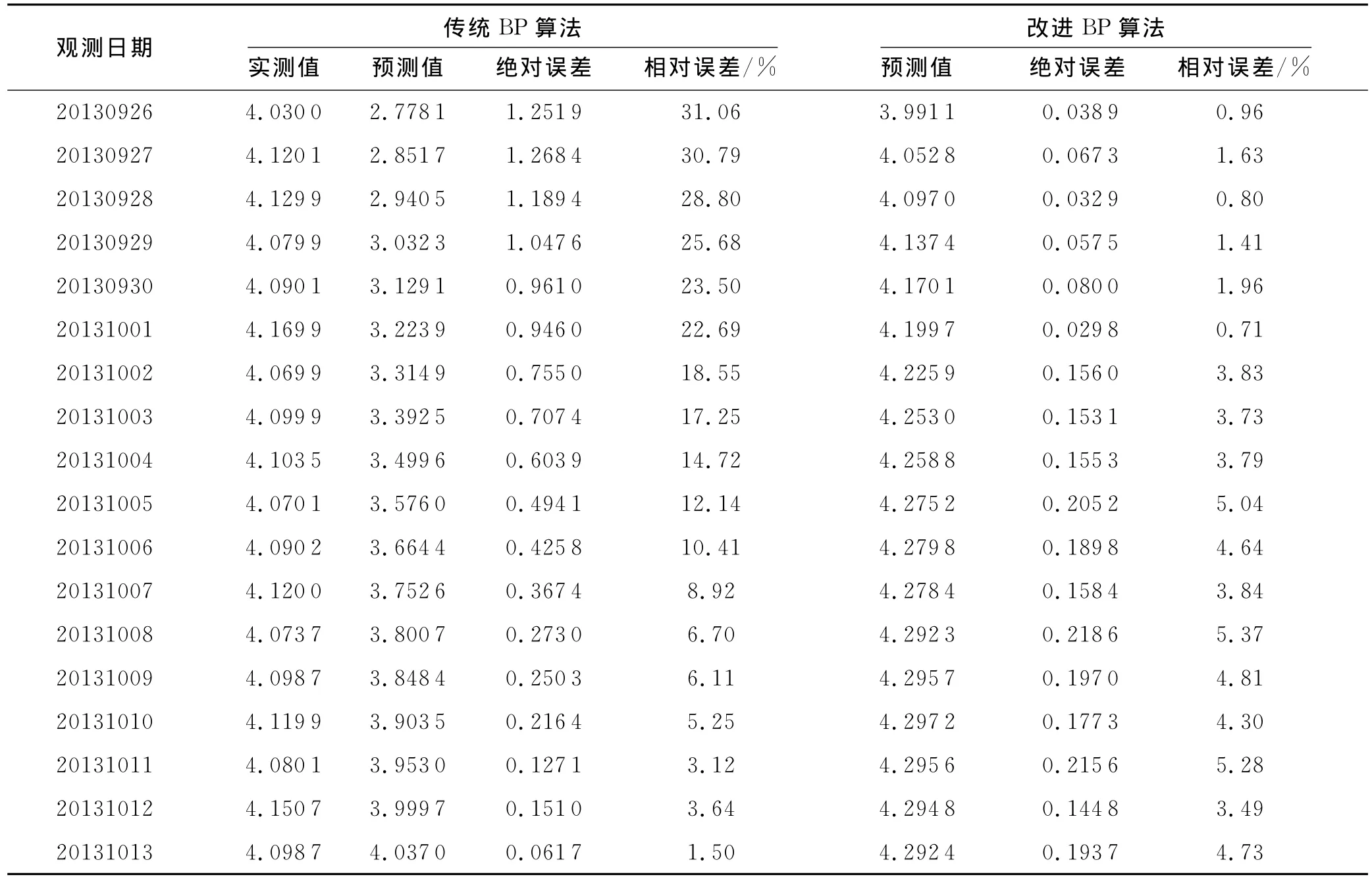
表1 径向位移预测精度对比

由表1可见，在采用传统的BP神经网络算法进行预测时，前期数据差值较大，绝对误差最大大于1 mm，相对误差最大达到31.06%.而后期数据预测效果较好，相对误差在5%以下.改进后的BP神经网络模型在整体预测精度上都大大提高，尤其在前期，绝对误差降低1mm，误差值均在1mm以下，相对误差控制在2%以下.结合图3分析原因，可见改进前的BP神经网络预测值呈早期迅速增长，后期趋于平稳的图形特征.这与训练数据本身以及坝前水位变化（图2）的前升后平的变化趋势是相吻合的.但这并不适用于预测点近期平稳上扬的数据结构.而改进后的BP神经网络模型依旧保持了上升的结构趋势，但是由于引入了遗忘函数，前期数据对整体数据的影响权重随时间序列降低，预测点近期数据影响权重相对较大，因而预测值不仅与预测点近期总体缓慢上扬的数据变化趋势相符，而且减弱了前期数据上升的速率，显示出平稳上扬的真实的数据变化规律.这种平稳上扬的趋势恰好与预测点近期的数据趋势相似，使得时间序列前3个点的相对误差从31.06%降低为不到2%，预测精度得到了明显的提高.而后期预测点也保持了相对较高的预测精度，相对误差在5.37%以下.这证明了引入遗忘函数的BP神经网络在蓄水期大坝安全监测模型的应用在理论上与有依据的，在实践中可以大大提高预测精度.

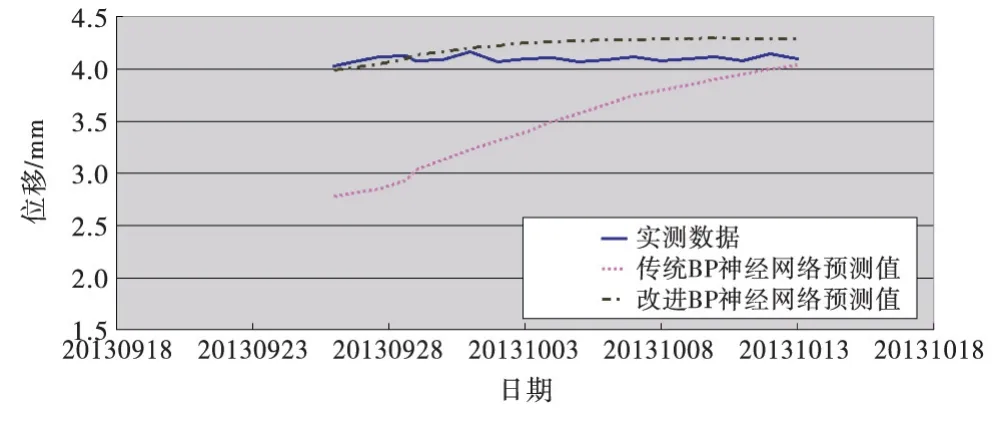
图3 径向位移实测与预测过程线对比

5 结 语

大坝蓄水初期，坝体性态随着水位不断升高而不断变化.传统的BP神经网络模型对这一变化不能给予准确及时的反应.本文应用改进的BP神经网络算法对某坝位移监测点径向位移进行资料分析，应用引入了遗忘因子的BP神经网络算法对监测数据进行了训练并预测，从预测结果可见，改进的BP神经网络算法可以对蓄水期大坝的性态变化进行实时更新，误差范围在0.8%至5.37%之间，相对于改进前的BP神经网络，将监测指标精度提高了约1mm，提高了预测效果，更适用于蓄水初期大坝监测的资料分析.

［1］ 吴中如.水工建筑物安全监控理论及其应用［M］.北京：高等教育出版社，2003.

［2］ 包腾飞，吴中如，顾冲时.基于统计模型与混沌理论的大坝安全监测混合预测模型［J］.河海大学学报：自然科学版，2003，31（5）：534－538.

［3］ 赵 斌，吴中如，张爱玲.BP模型在大坝安全监测预报中的应用［J］.大坝观测与土工测试，1999（6）：1－4.

［4］ 吴邦彬，陈 兰，葛 萃.改进的非等间距 GM（1，1）模型在大坝沉降分析中的应用［J］.水电能源科学，2012（6）：95－97.

［5］ 于 鹏，顾冲时.大坝安全监测的组合预测模型［J］.人民黄河，2006，28（1）：67－68，72.

［6］ 李 翔.从复杂到有序：神经网络智能控制理论新进展［M］.上海：上海交通大学出版社，2006.

［7］ 顾冲时，吴中如.大坝与坝基安全监控理论和方法及其应用［M］.南京：河海大学出版社，2006.

［8］ 杨庆春，李子阳.大坝蓄水期监测资料的时变分析模型［J］.水电自动化与大坝监测，2009，33（1）：54－56.

［9］ 叶 强，卢 涛，李一军.遗忘神经网络模型及其BP算法［J］.计算机工程，2004，29（20）：135－136.

［10］翁静君，华锡生.改进的BP神经网络在大坝安全监控中的应用［J］.水电自动化与大坝监测，2006，30（4）：62－65.

［11］赵二峰，刘敬洋，朱 凯.重力坝基岩力学时变特性随机动态分析模型［J］.武汉大学学报：工学版，2013（1）：89－94.