用“物理补偿法”突破数学积分的限制*
2014-10-21孙万军
孙万军
(江苏省六合高级中学,江苏 南京 211500)
现用普通高中课程标准实验教科书物理选修3-2(人民教育出版社)第5章第2节给出了正弦交变电流的有效值与其最大值之间的关系和.由于高中学生的知识水平所限以及《高中物理课程标准》中对正弦交变电流的有效值与其最大值之间关系的证明不作更高要求,笔者在课堂上对此并不做过多拓展.但在高三复习过程中,笔者发现很多学生对此问题的探讨具有浓厚兴趣;却因知识层次所限,苦于不知如何推导得出两者之间的关系而苦恼.传统的证明方法是运用高等数学中微积分的方法,但这不符合中学物理的教学实际.那么,有没有什么方法能突破这个限制呢?答案是肯定的.笔者在课余时间,对学有余力(参加奥赛)的学生,运用了高等数学中微积分的方法和中学物理中的“补偿法”,结合中学物理教学实际对正弦交流电的有效值与其最大值之间的关系进行了推导,从而消除了学生的疑惑;顺势把两种方法做了对比,让学生体会“物理补偿法”在此的“妙用”,并希望以此进一步引导学生学会运用类似方法提高解决相关物理问题的能力,增加学生的物理学科素养.
交变电流的有效值是根据电流的热效应来规定的,让交变电流和恒定电流通过相同阻值的电阻,如果它们在交变电流的一个周期内产生的热量相等,就把这一恒定电流的数值叫做这一交变电流的有效值.
方法1:数学积分法.
如图1所示的交变电流,它的瞬时表达式为u=Umsinωt,其中.在一个周期内产生的热量可表达为
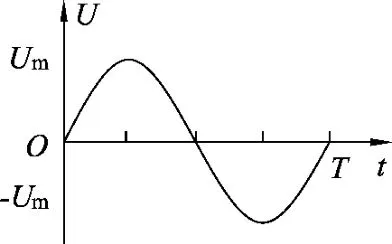
图1

由于Um、R为常量,可拿到积分号前面,故

注意到:2sin2θ=1-cos2θ,故上式可改写为
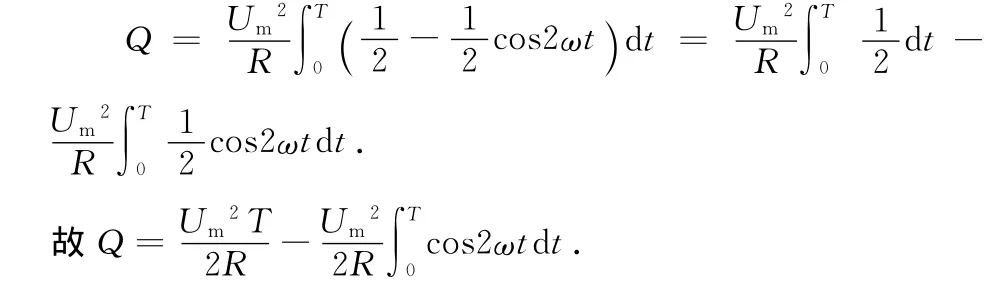


方法2:物理补偿法.
假设有两个交变电压,其变化规律如图2、图3所示,它们的最大值与周期都相同,它们的瞬时表达式分别为u=Usinωt、u=Ucosωt,其中把它们分别加在1m2m两个阻值相同的电阻上,设电阻的阻值为R,由于电流的热效应与电流的方向及先后作用的时间顺序无关,故在一个周期内两个交变电流产生的焦耳热相同,设都为Q,产生的总的焦耳热Q总=2Q.设它们交变电压的有效值为U,则有
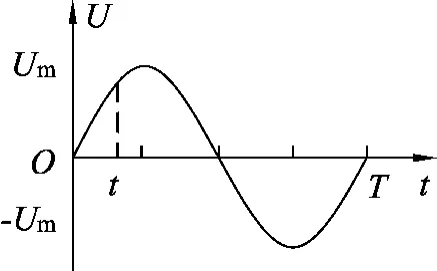
图2
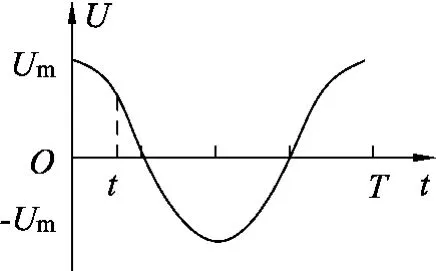
图3

另外,在任一时刻t,这两个电阻上的热功率分别为

两个电阻上总的发热功率为
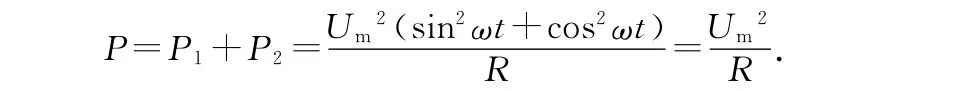
可以看出,两个电阻上总的发热功率是一定值,与时刻t无关,所以在一个周期内两个电阻上总的发热量为

方法对比:在介绍完两种方法后,笔者让学生对两种方法作出评价.学生普遍认为数学方法虽然很“高深”(因为高中阶段对微积分不作高要求),但显得比较“古板”;而对物理方法是大加赞赏,认为物理方法巧妙灵活,有明显的物理意义.
结束语:在高中物理中,有很多问题既可以用数学方法求解,也可以用物理方法求解(其实,数学方法中含有物理思想,物理方法中也含有数学成份.这里是指侧重数学方法和侧重物理方法).当两种方法都可以解决问题时,建议物理教师先采用数学方法,这种方法逻辑性强,是探究未知领域的根本方法,有较强的说服力,能让学生心服口服,但物理意义不明显;再运用物理方法求解,让学生体会物理方法求解问题的巧妙性,加深对物理过程的认识和理解.在平时的练习和考试中,如果遇到相关问题,应鼓励学生首选物理方法.
