钢桁架结构损伤识别的频响函数曲率法

朱新圆， 阿肯江·托呼提

(新疆大学建筑工程学院，新疆 乌鲁木齐 830047)

0 引言

结构损伤检测的提出是伴随着结构物的诞生而产生的，各种工程结构在投入使用后，由于环境的作用，会使结构存在裂缝、变形、腐蚀等损伤。结构的损伤可能会引起工程的倒塌，给人员生命安全和经济方面都造成巨大的损失，因此结构的损伤识别研究一直都是国际上的研究热点[1]。

一般而言，结构损伤识别需要解决4个层次的问题;①判断结构是否存在损伤;② 判断结构损伤位置;③判断结构损伤程度;④ 评估结构的剩余寿命。经过十几年的研究，结构损伤识别已经成为结构状态评估的重要组成部分，各国学者们提出了多种损伤识别方法。Pandey等[2]最早提出用模态参数去检测损伤，Sampaio[3]在此基础上提出了用频响函数检测损伤，姜增国[4]提出频响函数曲率比用于结构的损伤识别，由于频响函数比其他的模态参数包含更多的信息[5]，并且频响函数对结构损伤比较敏感，特别是在共振峰附近，能够准确地反映结构的动力特性，在用于损伤检测时其有效性和精确性较好。因此本文选用频响函数为损伤检测的指标。

目前钢结构的建筑物越来越多，大型桥梁以及钢结构建筑物中钢桁架的使用也越来越普遍，钢桁架结构的损伤检测技术则变得十分必要[6]，大量学者对桁架结构损伤检测进行研究，张丽梅等[7]提出柔度曲率幅值突变系数法对钢桁架进行检测，杨秋伟[8]提出了利用不完整测量的模态数据检测桁架结构损伤的方法，杜永峰等[9]对基于应变模态的桁架结构损伤指标进行研究，万璞佳[10]将模态分析和神经网络技术结合用于框架结构的损伤识别。王万平[11]对桁架结构的损伤识别提出了数据融合方法，并验证了该方法的有效性。李永梅等[12]用单元模态应变差法对桁架结构进行损伤识别，蔡小双等[13]提出了一种基于参与力向量理论的桁架结构损伤能识别方法，冯坤等[14]针对三维桁架提出了轴向模态应变能比法。然而桁架结构的杆件较多，因此准确定位桁架结构的杆件损伤位置则变得十分重要。本文用损伤识别指标精确地定位出结构损伤杆件出现的位置，即定位是上弦杆件、下弦杆件、斜腹杆件还是竖腹杆件出现损伤，并且能够判断出损伤的程度。

1 理论依据

结构在频率ω时所对应的频响函数曲率[3]为

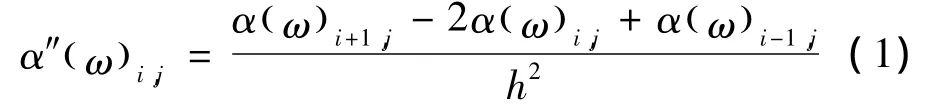
式中:αi，j是在j点施加力，在i点测得的位移响应。选频率范围内的频响函数曲率为

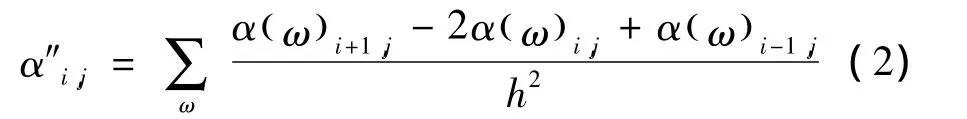
频率为ω时所对应的频响函数曲率差[3]为

式中:α″d(ω)i，j为损伤结构的频响函数曲率;α″(ω)i，j为完好结构的频响函数曲率。在所选频率范围内的频响函数曲率差为频率为ω时所对应的频响函数曲率比[4]为

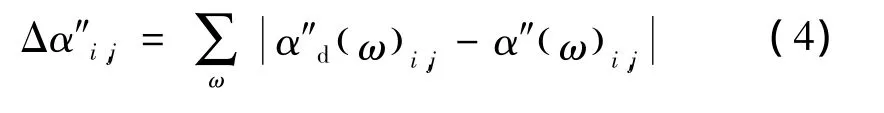
式中:α″d(ω)i，j为损伤结构的频响函数曲率;α″(ω)i，j为完好结构的频响函数曲率。在所选频率范围内的频响函数曲率比为

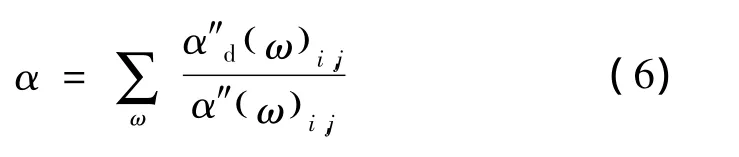
2 数值模拟

图1所示为一个二维桁架结构的有限元模型，结构长5 m，高0.5 m，共有22个节点，弹性模量为210 GPa，横截面积为3 000 mm2，材料密度为7 800 kg/m3。损伤情况分别为:①单处损伤工况。4～5损伤20%，40%，60%，80%;15 ～16 损伤20%，40%，60%，80%;5～15损伤20%，40%，60%，80%;4～15损伤20%，40%，60%，80%。② 多处损伤工况。3～4，7～8损伤20%，40%，60%，80%;3 ～4，18 ～19 损伤20%，40%，60%，80%;3 ～4，7～19 损伤20%，40%，60%，80%;3～4，8 ～19 损伤20%，40%，60%，80%。

图1 二维桁架结构有限元模型

2.1 单处损伤考虑不同损伤程度

结构为悬挑结构，检测点为下弦上的所有节点，因此结构的频响函数曲率和频响函数曲率差呈下降的趋势，但是在结构存在损伤的位置会产生突变，而频响函数曲率比呈水平趋势，在损伤位置产生突变。频响函数曲率比比频响函数曲率与频响函数曲率差更直观，不需要考虑结构的形式。

下弦杆4～5杆件4种不同损伤程度下的频响函数曲率、曲率差以及曲率比如图2～4所示。从图中可见，结构在4点处产生突变，并且随着损伤程度的变化，突变程度也发生相应的变化，但是频响函数曲率差对于小程度的损伤不敏感。

当曲线在4～5之间产生突变时，可能涉及损伤的杆件有4～5杆件，15～16杆，4～15杆，5～16杆，5～15杆，不能够精确地检测出到底是哪一根杆件损伤会使检测结果精确性降低，因此可以根据曲线的变化点来尽可能得缩小可能损伤范围或者精确损伤位置。

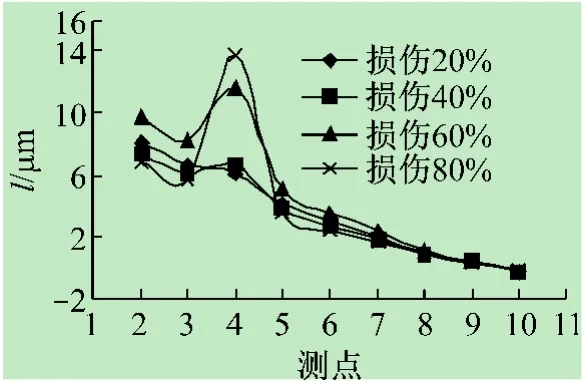
图2 4～5不同损伤程度频响函数曲率

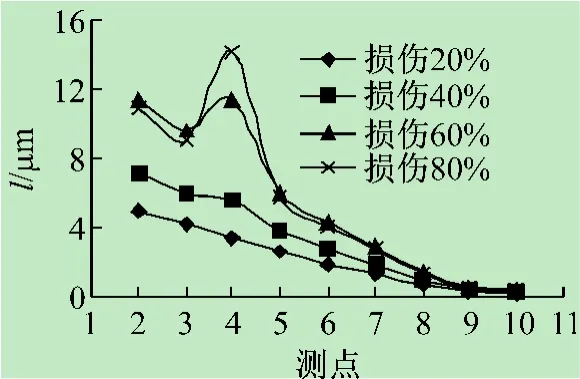
图3 4～5不同损伤程度频响函数曲率差

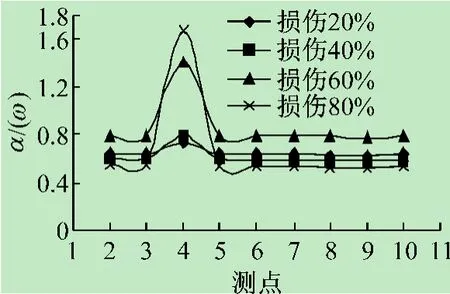
图4 4～5不同损伤程度频响函数曲率比

4～5之间产生损伤，会影响4，5点的频率响应，但是在5节点处有两根斜腹杆的作用，因此只在4点有突变。所以当4点产生突变时，可以缩小它的损伤区域为4～5杆件或是3～4杆件。在检测的过程中，我们可以通过曲线的变化来缩小可能损伤的范围，增加检测结果的精确性。

上弦杆15～16在4种程度的损伤下，检测结果如图5～7所示。由于15点有两根斜腹杆作用，因此只在16点有突变，即反映在下弦节点5点上。3个损伤识别指标均在5点在处产生突变，并且随着损伤程度的变化产生相应的变化。因此5点产生突变可以缩小损伤杆件为15～16杆或者16～17杆。在检测上弦杆件损伤情况时，频响函数曲率差对于小程度的损伤不敏感。

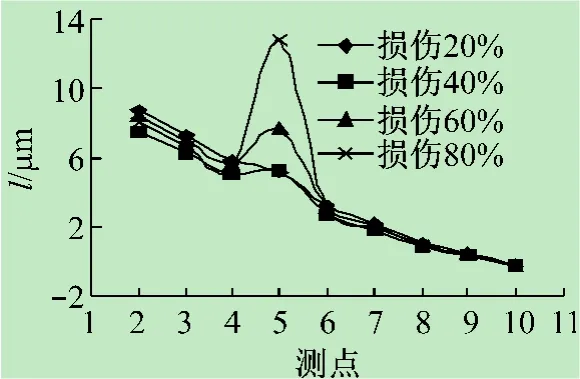
图5 15～16不同损伤程度频响函数曲率

图6 15～16杆不同损伤程度频响函数曲率差

图7 15～16杆不同损伤程度频响函数曲率比

斜腹杆5～15损伤时，损伤检测结果如图8～10所示。频响函数曲率与频响函数曲率比在4点产生正突变，在5点产生负突变，并且随着损伤程度的增加，突变增加，频响函数曲率差只在5点产生突变。因此当在两点检测区域，一点出现正突变，一点出现负突变时，我们可以精确其损伤位置为斜腹杆。

图8 5～15杆不同损伤程度频响函数曲率

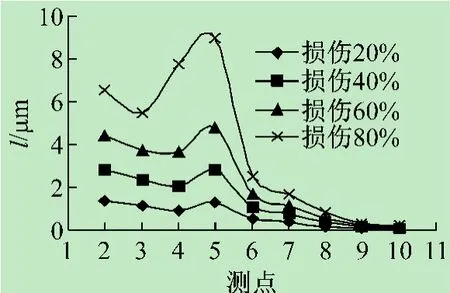
图9 5～15杆不同损伤程度频响函数曲率差

图10 5～15杆不同损伤程度频响函数曲率比

当竖腹杆4～15损伤时，检测结果如图11～13所示。频响函数曲率没有变化，因此频响函数曲率对竖腹杆的损伤检测不适用。频响函数曲率差只在4点产生突变，而频响函数曲率比在3点与5点产生正突变，在4点产生负突变，4点的负突变是3点与5点正突变的2～3倍。因此当频响函数曲率比出现如图12所示的曲线时，我们可以精确其损伤的杆件为4～15杆。

2.2 多处位置损伤

结构多处损伤情况下结构得到检测结果如图14～25所示，可以通过其检测曲线判断结构的损伤位置，频响函数曲率与频响函数曲率差对于不同位置损伤程度的检测，不能用曲线突变大小来判断，损伤区域越靠近支座的位置，频响函数曲率与频响函数曲率差对损伤就越敏感。频响函数曲率比不受支座位置的影响，不仅能够检测出结构损伤的位置、损伤程度，而且可以精确定位损伤的杆件。

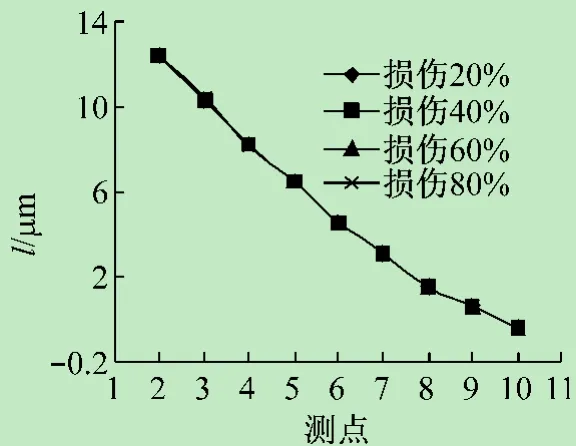
图11 4～15杆不同损伤程度频响函数曲率

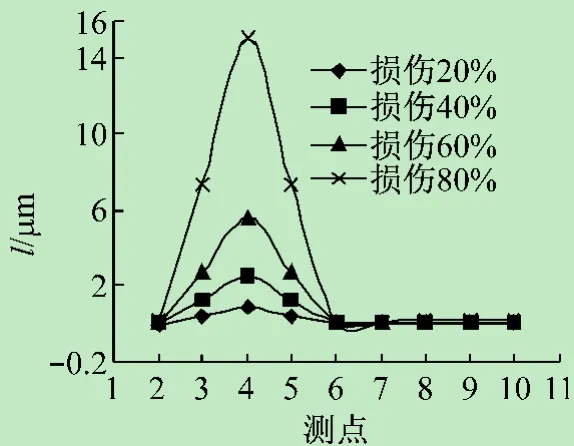
图12 4～15杆不同损伤程度频响函数曲率差

图13 4～15杆不同损伤程度频响函数曲率比

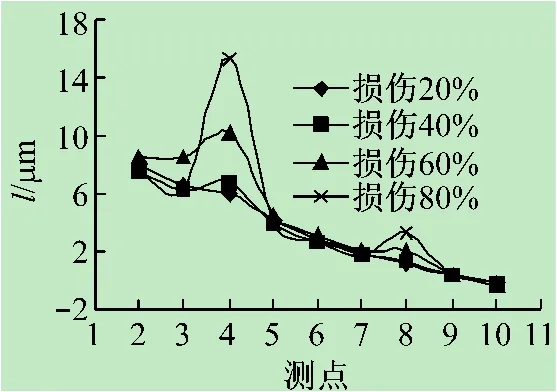
图14 3～4，7～8杆损伤频响函数曲率

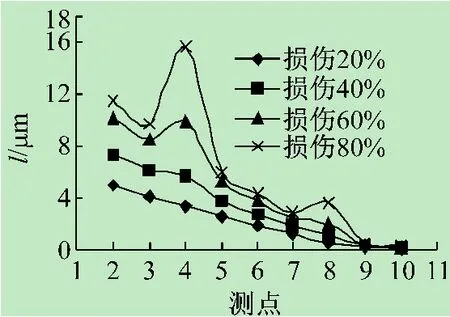
图15 3～4，7～8杆损伤频响函数曲率差

图16 3～4，7～8杆损伤频响函数曲率比

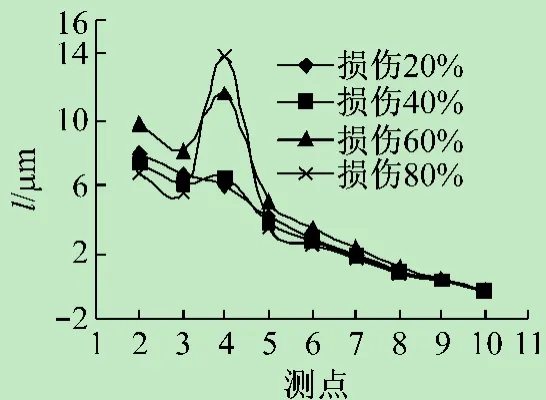
图17 3～4，7～18杆损伤频响函数曲率

图18 3～4，7～18杆损伤频响函数曲率差

图20 3～4，7～19杆损伤频响函数曲率

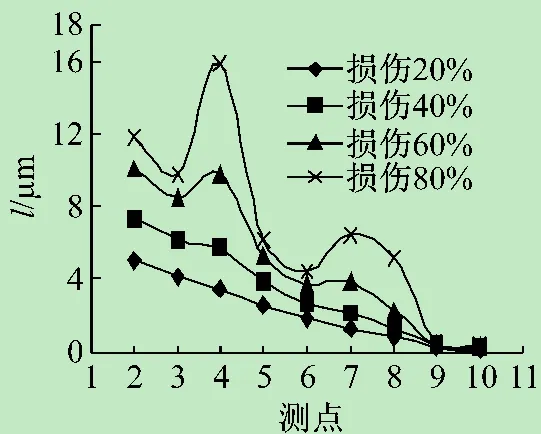
图21 3～4，7～19杆损伤频响函数曲率差

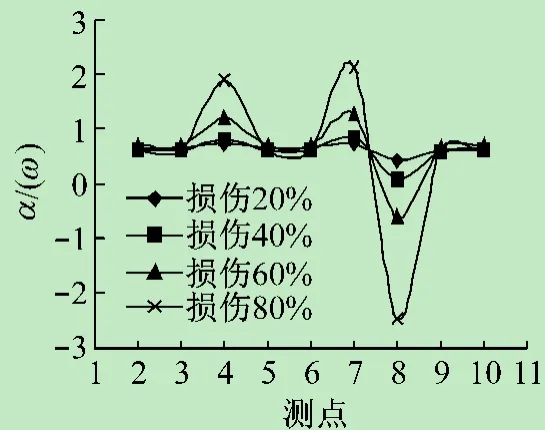
图22 3～4，7～19杆损伤频响函数曲率比

图23 3～4，18～19杆损伤频响函数曲率

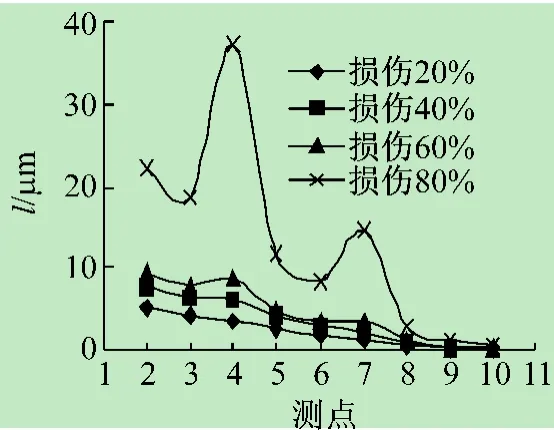
图24 3～4，18～19杆损伤频响函数曲率差

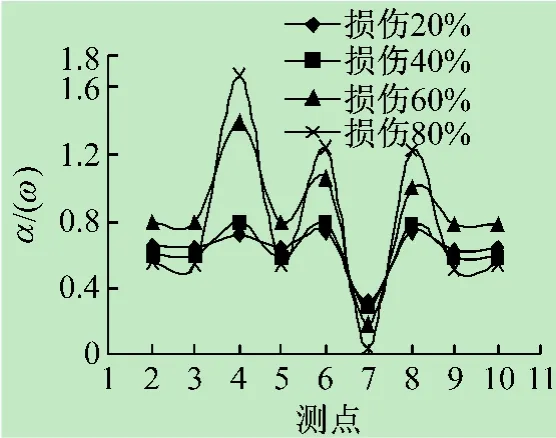
图19 3～4，7～18杆损伤频响函数曲率比

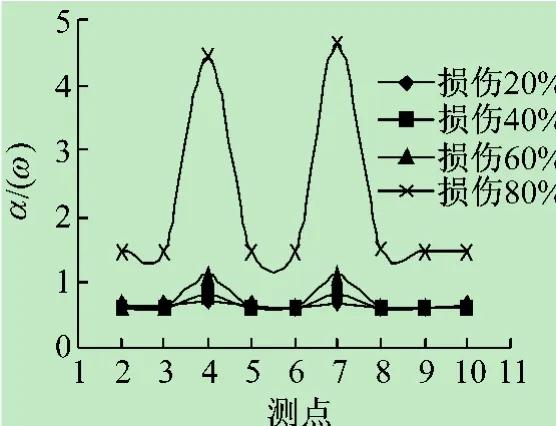
图25 3～4，18～19杆损伤频响函数曲率比

3 结语

钢桁架结构损伤的检测精确性最好的损伤识别指标是频响函数曲率比，不仅能通过损伤检测确定损伤的位置，并且可以判定结构的损伤程度。频响函数曲率可以检测出上弦杆、下弦杆、斜腹杆的损伤位置以及损伤程度，但无法检测出结构竖腹杆的损伤情况。频响函数曲率差在进行损伤检测时，可以对检测出结构的损伤情况，但频响函数曲率差对小程度损伤进行检测时敏感性较低。

进行钢桁架的损伤检测时，可以根据频响函数曲率比的曲线图形判断出结构损伤具体出现在哪根杆件，对于上弦杆件和下弦杆件可以缩小可能损伤范围到2根杆件，对于斜腹杆和竖腹杆可以精确检测出其损伤的杆件。

多处损伤的钢桁架损伤检测通过频响函数都可以检测出其损伤位置，但是对于不同位置的损伤不能根据频响函数曲率和频响函数曲率差判断损伤程度，上述两个损伤识别指标受结构形式的影响，越靠近支座处对损伤越敏感，但是频响函数曲率比不受结构形式的影响，可以检测出结构的损伤程度以及精确损伤出现杆件的位置。

[1] 郭惠勇，李正良，彭 川.结构损伤识别动力技术的研究与进展[J].重庆建筑大学学报，2008，30(1):140-146.GUO Hui-yong，LIZheng-liang，PENG Chuan.Researchesand Advances in Structural Damage Dynamic Identification Technology[J].Journal of Chongqing Jianzhu University，2008，30(1):140-146.

[2] Pandey A K，Biswas M，Samman M M.Damage detection from change in curvature mode shapes.Journal of Sound and Vibration，1991，142，321-332.

[3] Sampaio R P C.Damage Detection Using the Frequency-Response-Function Curvature Method [J].Journal of Sound and Vibration，1999，226(5)，1029-1042.

[4] 姜增国，张 桢.基于应变频响函数曲率的结构损伤识别[J].建筑科学与工程学报，2009，26(4):40-43.JIANG Zeng-guo，ZHANG Zhen.Structural damage identification based on sfrf curvature[J].Journal of Architecture and Civil Engineering，2009，26(4):40-43.

[5] 汪之松，郭惠勇，李正良.基于频率响应的不同结构损伤识别方法研究[J].工程力学，2008，25(6):6-13.WANG Zhi-song，GUO Hui-yong，LIZheng-liang.Identification methods for different structural damage based on frequency response[J].Engineering Mechanics，2008，25(6):6-13.

[6] 李国东.钢结构损伤诊断实用方法研究[D].北京:中国地震局工程力学研究所，2010.

[7] 张丽梅，陈务军，杜守军，等.钢桁架结构损伤检测的柔度曲率幅值突变系数法[J].东南大学学报，2005，35(Sup.):133-138.ZHANG Li-mei，CHEN Wu-jun，DU Shou-jun，et al.Testing damage on the steel truss structure using the method of the sudden change coefficient of flexibility of curvature[J].Journal of Southeast University(Natural Science Edition)，2005，35(Sup.):133-138.

[8] 杨秋伟.不完整测量条件下检测桁架结构损伤的一种方法[J].机械强度，2010，32(1):001-004.YANG Qiu-wei.Damage detection for truss structures using incomplete modal parameters[J].Journal of Mechanical Strength，2010，32(1):001-004.

[9] 杜永峰，邵云飞.基于应变模态的桁架结构损伤指标研究[J].甘肃科学学报，2007，19(3):127-130.DU Yong-feng，SHAO Yun-fei.Study on damage of truss structure based on strain modal[J].Journal of Gansu Sciences，2007，19(3):127-130.

[10] 万璞佳，基于模态分析和神经网络技术的框架结构损伤识别研究[D].西安:西安建筑科技大学，2012.

[11] 王万平，翁光远，申 伟.桁架结构损伤的数据融合方法研究[J].工业建筑，2012，42(12):129-132.WANG Wan-ping，WENG Guang-yuan，SHEN Wei.Study on data fusion method for truss structure damage identification[J].Industrial Consturction，2012，42(12):129-132.

[12] 李永梅，郭 磊，孙国富，等.桁架结构损伤识别的单元模态应变差法[J].铁道学报，2010，32(6).LI Yong-mei，GUO Lei，SUN Guo-fu，et al.Identification of damage of truss structures using elemental modal strain method[J].Journal of the China Railway Society，2010，32(6).

[13] 蔡小双，纪国宜.基于残余力向量法的桁架结构损伤识别[J].工业建筑，2013，43(增刊):211-215.CAI Xiao-shuang，JI Guo-yi.A damaged identification method of truss structures based on residual force vector[J].Industrial Construction，2013，43(Sup.):211-215.

[14] 冯 坤，杨永春，郑 秩.基于轴向模态应变能比法的三维桁架结构损伤定位方法[J].振动与冲击，2013，32(12):169-174.FENG Kun，YANG Yong-chun，ZHENG Yi.Damagedetection method of a three-dimensional truss structure based on axial modal strain energy ratio[J].Journal of Vibration and Shock，2013，32(12):169-174.

[15] 张 军，刘建勋，徐 进，等.结构损伤诊断的模态柔度差曲率法[J].工程力学，2011，28(12):112-117.ZHANG Jun，LIU Jian-xun，XU Jin.Structural damage detection based on change in curvature of flexibility[J].Engineering Mechanics，2011，28(12):112-117.