流体力学在液压管路设计中的应用

康建喜

(咸阳陶瓷研究设计院 陕西 咸阳 712000)

前言

流体力学，是研究流体的力学运动规律及其应用的学科。其主要研究在各种力的作用下，流体本身的状态以及流体和固体壁面、流体和流体之间、流体与其他运动形态之间的相互作用的力学分支。在农业、工业、航天、军事及工程中具有重要的应用价值。本文主要介绍了某些流体力学在液压管路设计中的几点应用。在液压管道设计中，充分应用流体力学这门基础学科。

1 液压管道压力损失的种类

液压管道系统由若干管道与管接头、阀件等局部装置连接而成。管道系统主要有串联、并联和分支等几种结构形式，液体在流经管道系统时的能量损失工程上通常用压差形式表示，称为压力损失。压力损失由黏性摩擦阻力引起的沿程压力损失和由于流道形状变化(突然转弯，阀口)及流动方向变化因相互撞击和出现旋涡等所产生的局部压力损失组成。压力损失与液流的流态有关。

2 液体的2种流态及雷诺判据

液体在管道中流动时有层流和紊流2种流动状态(简称流态)。层流时，液体质点沿管轴呈线状或层状流动，而没有横向运动，互补掺混和干扰。紊流时，液体质点除了横向脉动还有相对于平均运动的反向运动，强烈搅混，质点之间相互碰撞，做混杂紊乱状态的流动，2种状态可用雷诺数来判别。

雷诺数Re是由管内的平均流速v、管道(或流道)的水力直径dH、液体的运动黏度μ这3个参数所组成的一个无因次数。

Re=vdH/μ=ρvdH/μ

式中:v——平均流速,m/s;

dH——水力直径,dH=4A/x,m;圆截面管道的水力直径dH与其管径d相同；

A——液体通流截面面积,m2;

x——通流截面的湿周长度,m;

υ——液体的运动黏度,m2/s;

ρ——液体密度,kg/m3;

μ——液体的动力粘度,Pa·s。

如果液流的雷诺数相同，则流动状态也相同。

水力直径的大小反映了管道或流道的通流能力，水力直径大，意味着液流和管壁的接触面积小，阻力小，通流能力大。在通流截面面积相同但形状各异的所有流道中，圆形截面管道的水力直径最大。

液体由层流转变为紊流时的雷诺数和由紊流转变为层流时的雷诺数是不相同的，前者称为上临界雷诺数Re上，后者称为下临界雷诺数Re下，Re上>Re下，因此一般都采用后者作为判别液流状态的依据，称为临界雷诺数Rec。当液流的实际雷诺数Re小于临界雷诺数Rec时，液体为层流；反之，为紊流。

常见液流管道的水力直径及临界雷诺数可以通过查相关的数据获得。在所有的液体流道中，光滑圆管的临界雷诺数最大为Rec=2 300。

3 沿程压力损失的计算

3.1 计算公式

管道中沿程压力损失△Pλ按照达西(Darcy)公式计算:

式中:λ——沿程阻力系数,是雷诺数Re和管道内壁粗糙度(△)的函数;

△——管内壁的绝对粗糙度,mm;△的数值与管壁材质有关;

L——管道长度,m。

3.2 沿程阻力系数λ

圆管沿程阻力系数λ的数值可以根据Re值及相对粗糙度△/d(△为管内壁的绝对粗糙度，△的数值与管道材质有关，请参见表1所示;d为管道直径)的值按表2相应的公式进行计算。

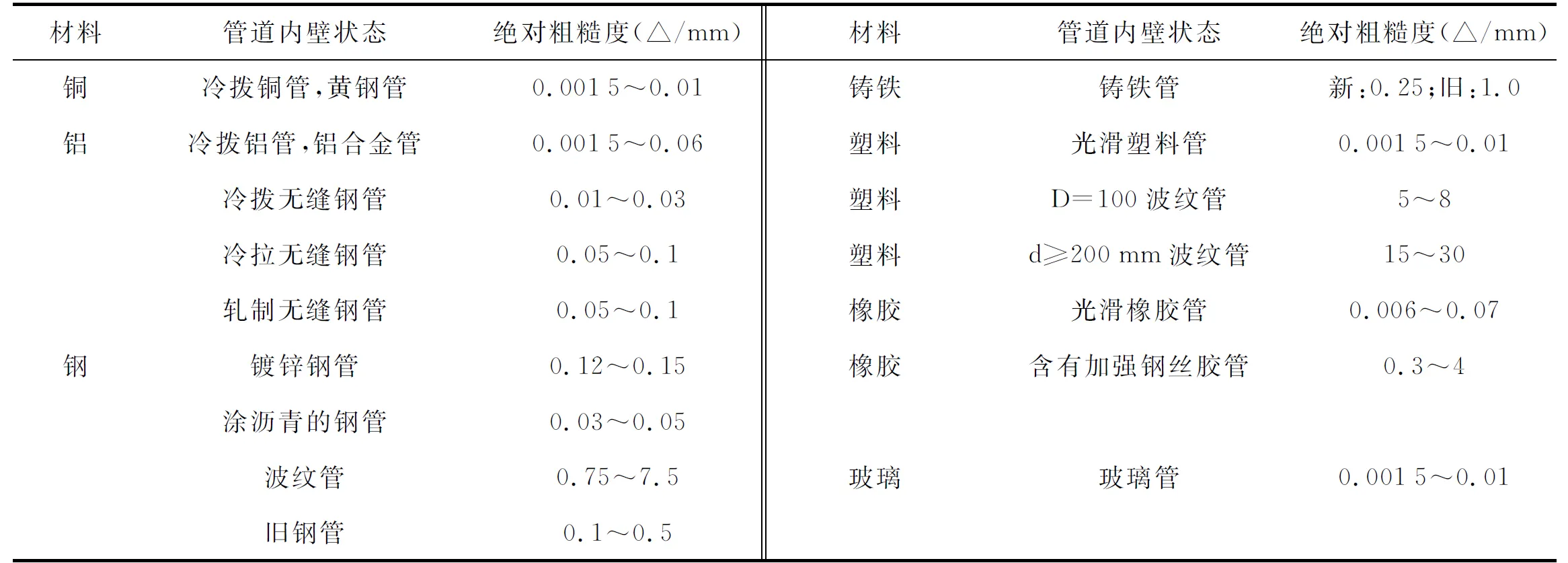
表1 不同材料管道的内壁绝对粗糙度△

表2 圆管沿程阻力系数λ计算公式

注：①层流时，λ仅与雷诺数Re有关，与相对粗糙度无关；②工程中处于层流到紊流过渡区很少，其λ可按光滑管紊流计算；③紧贴管壁处(简称近壁处)的液体受黏性切应力支配，液体质点的脉动受到限制，故称其为黏性底层；④黏性底层厚度大于绝对粗糙度称为光滑管紊流区，其λ仅与雷诺数Re有关，不受管壁粗糙度影响；⑤近壁处黏性底层厚度近似等于绝对粗糙度称为过渡区，其λ是雷诺数Re和管道内壁相对粗糙度d/△的函数，即λ=(Re，d/△)；⑥近壁处黏性底层厚度小于绝对粗糙度，称为粗燥管紊流区，管壁粗糙表面刺破近壁流层，粗糙度严重影响流动，其λ仅是管道内壁相对粗糙度d/△的函数。

对于非圆管的沿程阻力系数，可将λ公式中的d和Re公式的d换成水力直径dH，代入计算。

4 局部压力损失计算

4.1 计算公式

局部压力损失△Pξ一般按下式进行计算:

式中:ζ——局部阻力系数，其具体数值与局部阻力装置的类型和雷诺数有关;通常,当Re>105时,ζ与Re无关;

ρ——液体密度,kg/m3;

υ——液体的平均流速，m/s;v或为局部装置前，或为局部装置后管段的平均流速，它必须与局部阻力系数ζ相对应，除特别声明，通常指两平均流速中较高者。

4.2 局部阻力系数ζ

除断面扩大、缩小等个别局部阻力装置的局部阻力系数可用理论计算外，大部分局部阻力装置的阻力损失系数多由实验测出或由经验公式算出，且大部分是针对紊流而言。

4.2.1 断面扩大管道

1)突然扩大管道。设管道断面积由A1突然扩大成A2，1-1断面和2-2断面的平均流速分别为v1和v2,则局部压力损失△Pξ为:

当A2>>A1(例如液流由管道流入油箱的情况)，则有ζ1=1。

2)渐扩管道。渐扩管道的局部压力损失计算式用系数k来修正，即:

4.2.2 断面缩小时的压力损失

1)突然缩小管道。突然缩小管道的压力损失计算公式为:

式中:Cv——流速系数，为缩流断面上实际的平均流速vc与理想的平均流速v0之比；

Cc——断面收缩系数，为缩流断面积A1与管道断面积A2之比。

断面突然缩小管道系数Cc、Cv及ξ见表3。

表3 断面突然缩小管道的Cc、Cv及ξ值

2)渐缩管道。渐缩管道的压力损失也按渐扩管的公式进行计算，但其中ξ的计算公式为:

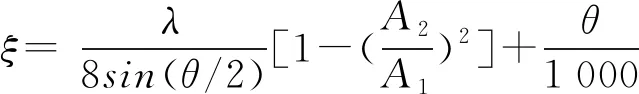
式中：λ——变径后的沿程阻力系数。

当θ角较小且过渡段圆滑时,ξ=0.05～0.005,渐缩管道的压力损失系数也可由图查出。

4.2.3 弯管的局部压力损失

弯管的流动会产生双漩窝形式的二次流动,弯度较大时液体会从管壁剥离。其流动现象十分复杂,只能用实验方法求得其阻力系数ξ。

液压系统常见的是圆滑弯管,其总压力损失△P=ξ(ρv2/2)中的损失系数ξ(包含弯管局部的磨擦损失)可按下列公式算出。这些公式的适用范围为：弯管中心的曲率半径R和管半径r之比R/r>2，且2×104

在Re(r/R)2<91时，ξ=0.008 73aλcθ(R/r)

在Re(r/R)2>91时，ξ=0.002 41aθRe-0.17(R/r)0.84

式中: θ——弯管方向变化角;

λc——无剥离现象的缓慢弯管的管摩擦系数。

45°弯管：α=1+14.2(r/R)1.47

90°弯管：α=0.95+17.2(r/R)1.96

R/r<19.7,α=1 ,

R/r>19.7

180°弯管：α=1+116(r/R)4.52

4.2.4 液体流经管道分支处的局部阻力损失

4.2.5 流体流经液压阀及辅件的局部压力损失

液压阀及辅件上的局部阻力系数可参照相关的对照表，其中各种阀口的阻力系数因开口量的不同而有较大的变动幅度，开口量较大时取小值，开口量较小时取大值，也可根据通过阀的实际流量直接计算其局部压力损失△Pv。

△Pv=△Ps(q/qs)2

式中:q——阀的实际流量;

qs——阀的额定流量;

△Ps——阀在额定流量qs下的压力损失。

5 管路系统压力损失的叠加

一个液压系统总的压力损失应为所有沿程压力损失与所有局部压力损失之和，即:

式△Pv=△Ps(q/qs)2适用于两相邻局部阻力装置间的距离大于管道内径10～20倍的场合，否则计算出来的压力损失值比实际数值小。其原因是进口起始段的影响，即局部障碍距离太小，通过第一个局部阻力装置后的液体尚未稳定就进入第二个局部阻力装置，从而造成更强烈的液流扰动，使阻力系数要高于正常值的2～3倍。

液压系统中的压力损失不仅耗费功率，还将使系统油温增高，工况恶化。因此，在液压系统设计中应设法减小压力损失，其措施包括采用合适黏度的液体及流速，力求管子内壁光滑，尽量减少连接管的长度和局部阻力装置，选用压降小的控制阀等。

6 结语

流体力学作为一门基础学科，随着各个学科的交叉及边沿学科的出现，将来会越来越多地应用在各个工程设计当中，在液压传动中的应用只是其中一个范例。在液压传动当中，由于工作介质为液体，决定了流体力学的应用广泛。在液压传动系统的分析与设计中，只有通过合理的计算，选择适合某一个液压系统合适的管路系统，阀件系统，才能使该系统能够稳定、可靠地运行，才能实现较小的经济投资，较低的运行成本。所有这些都需要流体力学的基本理论知识，用流体力学的方法来假设液压介质或液压油在液压系统中的某种流动状态，从而确定液压介质或液压油在系统中的运行状态，工作状态。在某些特殊需要的状态下，要对液压介质的运行进行仿真，模拟流体在有载荷下的状态，从而对各种参数进行验证，对某些参数进行再次修正，使得系统能够在一个最佳的状态下运行。