扩散模型和凝聚模型耦合作用下胶体凝聚动力学的Monte Carlo模拟研究

熊海灵 杨志敏 李 航

(1西南大学计算机与信息科学学院,重庆 400715;2西南大学土壤多尺度界面过程与调控重庆市重点实验室,重庆 400715;3西南大学资源环境学院,重庆 400715;4西南大学三峡库区生态环境教育部重点实验室,重庆 400715）

1 引言

胶体稳定性的研究在胶体科学中一直占有很重要的地位,Smoluchowski方程对胶体凝聚动力学的描述是建立在平均场近似的基础上的.实验上可测量胶体凝聚的速率常数,但无法据此分析团簇大小对速率常数的影响.胶体稳定性理论(Derjaguin-Landau-Verwey-Overbeek(DLVO））虽可对胶体凝聚速率常数作定性解释,但仍难以就团簇结构对速率常数的影响规律作出定量处理.1

Monte Carlo模拟方法是近年来发展起来的一种可用于研究胶体颗粒相互作用的计算机模拟方法.2,3目前胶粒凝聚的Monte Carlo模拟最活跃的领域主要在四个方面,4即:胶体理论的进展及计算方法的改进,热力学性质的模拟,动力学性质的模拟,团簇结构性质和形貌特征的模拟.动力学性质的模拟包括使用Smoluchowski方程对体系中每一个颗粒与其它颗粒可能进行的“反应”都作微观模拟,5也包括了其它形式的模拟.6-11由于体系的复杂性,基于Smoluchowski方程的模型虽然有微观机理方面的正确性,但其准确性不足;其它形式的模型虽然准确性较好,但普遍适应性欠佳,模型的物理意义也不明确.目前还没有一个模型既能明确地表达体系的微观机理,又有宏观上的普遍适应性.4分析原因主要有以下两点:(1）基于Smoluchowski方程的模型需要建立在6条假设1的基础上,这种基于微观表象强加于模型上的约束条件,严重影响了它在真实系统中的应用,其中对所有碰撞都导致粘结,所有颗粒在碰撞前后均为实心球体的假设是该模型与实际相差太大的最根本原因;(2）其它形式的模型2,6-8,12-15大多还是从Smoluchowski方程的模型出发,孤立地解决那6条假设所带来的问题.如有的模型考虑到凝聚过程中形成的团簇不是一个实心的、规则的球体,而人为地设定一个固定的形状因子,显然这样一个形状因子难以描绘团簇的实际特征,也就更难以确定团簇的扩散机理.有的模型为了解决一碰撞就粘结的问题,也是人为地设定一个较小的凝聚概率,显然这也无法表达不断发展变化的各种大小的团簇的凝聚机理.

实际上,胶体的凝聚动力学行为及团簇的形貌特征是直接受团簇的扩散机理以及凝聚机理影响的,只有确定了正确的扩散模型和凝聚模型,模拟的结果才可能准确,模型也才能有较好的适应性.

目前在众多模型中,7,8,15,16团簇-团簇凝聚(CCA）模型可以较好地用来描述胶粒凝聚的过程.17即该模型可以用来描述胶粒先聚合成小的结构(团簇）,这些小的结构再经多次聚合而形成越来越大的结构体的过程.以CCA模型为基础,胶粒凝聚过程一般认为可分为两类:扩散控制过程的扩散置限团簇凝聚(DLCA）与反应控制过程的反应置限团簇凝聚(RLCA）.18-20在扩散控制的凝聚中,两个粒子(胶体颗粒或团簇）一旦相遇即发生凝聚.所以,胶体颗粒的凝聚速度由碰撞概率决定,一切影响颗粒移动速度的因素都影响碰撞概率,从而影响凝聚速度.而在反应控制过程中相碰撞的两个胶体颗粒或团簇不是一碰撞就凝聚,而是以一定的、概率值小于1的概率发生凝聚,这个概率可被称为有效碰撞概率.此时胶体凝聚速度不仅受碰撞概率所制约,而且受有效碰撞概率所制约.由此可以看出,由于RLCA过程的凝聚概率等于碰撞概率与有效碰撞概率的乘积,所以相对来说RLCA过程是一种慢速进行的凝聚过程.不同体系及同一体系不同条件下的碰撞概率和有效碰撞概率具有较大的差异.21

然而,问题的关键是如何确定碰撞概率和有效碰撞概率,也就是说在利用CCA模型进行计算机模拟时如何确定扩散模型和凝聚模型.这两个模型都要求模拟过程既能联系诸多影响胶粒凝聚的热力学条件,又要能体现胶体科学中已经被人们普遍认同的慢速凝聚和快速凝聚之间的联系,这样才能实现模型不但准确性,普适性好,而且模型的物理意义也明确.

多年来,人们为确定这两个模型作了艰苦的努力,6-8直到分形理论5,9,13,22的诞生及其在胶体科学中的应用,才使问题有了转机.现在许多实验表明,23-28胶体颗粒的凝聚体是分形结构,所以,传统的模型应该就分形特性的加入进行调整.Ziff等1证明,如果考虑到团簇的分形特性,Smoluchowski方程可以比较准确地表达胶体的凝聚动力学.根据Kirkwood-Riseman理论,7,8,12对于不规则形状的颗粒或团簇,其移动的布朗扩散系数Ds与其质量s(实际可以用团簇中的粒子数表达）的关系可以用下式描述:

其中D0是单个粒子的扩散系数,γ则称为扩散指数(diffusivity exponent）.从公式(1）可以看出,对于γ=0的情况,实际就是大小团簇的扩散系数相同,与团簇的质量无关;对于γ＜0的情况,则对应小团簇比大团簇移动快;对于γ＞0的情况,则对应小团簇比大团簇移动慢.已有文献5,6,8,15表明,当γ足够大时,在CCA模型下会得到与DLA模型类似的凝聚体.DLA模型所对应的凝聚体是在有“凝聚中心”的前提下产生的,5,6,8,15但为什么会产生“凝聚中心”?为什么会出现小团簇比大团簇移动慢的现象?也就是说γ＞0的物理意义何在?在此以前还未见文献报道.对于这些问题,本研究试图给一个合理的解释.

根据Meakin的研究,8,15碰撞在一起的两个颗粒或团簇粘结在一起的概率Pij可用下式描述:

其中i、j分别代表碰撞在一起的两个颗粒或团簇的质量,σ称为凝聚概率指数(sticking probability exponent）,P0表示两个初级粒子由于布朗运动碰撞而粘结在一起的概率,显然P0≤1,当Pij＞1时则被设置为1.从公式(2）可以看出,对于σ=0的情况,实际就是大小团簇碰撞的有效碰撞概率相同,与团簇的质量无关;对于σ＞0的情况,团簇间的有效碰撞概率随团簇质量的增加而增大;对于σ＜0的情况,团簇间的有效碰撞概率随团簇质量的增加而减小.以前的研究2,8,15大多集中在σ≥0的情况,关于σ＜0情况是否有明确的物理意义的探讨,至今也还未见报道.

Meakin等6分别利用公式(1）、(2）,从团簇的移动性和团簇的凝聚概率的角度,单独考察了胶粒凝聚过程中团簇大小的分布,发现团簇大小的分布具有标度性质.但Ziff等1指出仅从团簇的大小分布来证明模型的正确性是不够的,由此来研究胶体的凝聚动力学行为也是不全面的.因此必须比较系统地考虑团簇的移动性和团簇碰撞的凝聚概率对胶体凝聚动力学的影响.

先期的研究已表明虽然各种胶体的特性不一样,但其凝聚的机理与动力学却有相似之处.20,21,29,30因此本研究将凝聚过程动力学的各个影响因素的作用归结为扩散指数和凝聚概率指数的作用,通过调整扩散指数和凝聚概率指数大小来探讨胶体凝聚的动力学过程.

2 模拟研究方法

模拟在边长为100个单位胶粒直径长度的立方体中进行,立方体被划分成边长为单位胶粒直径长度的小立方体格子(总共1003个）,初始时N0=10000个粒子被无重叠地随机置放在三维网格中,粒子在X、Y、Z轴的6个方向上做随机运动.模拟中胶粒或团簇移动、碰撞、粘结的规则与文献6,17相似,模拟时间按式(3）增长:12

其中,Dmax是当前体系中团簇(含单粒）的最大扩散系数,是在模拟过程中进行统计比较得出的,Nc是当前体系中的团簇数(包括单粒）,由此得到模拟实验的时间的标度是在相同环境条件下单个胶体粒子移动单位胶粒直径所需的时间.模拟中考察不同扩散指数和凝聚概率指数及其组合对凝聚过程的影响.

对公式(1）、(2）而言,以前的研究结果8,12大多只是考虑了γ≤0和σ＞0时的情况,因为这两种情况与实际的胶体体系在常规情况下的凝聚特征是基本相符的.本模拟实验为了比较全面地研究这两个因子的影响,以及有效地表征前人提出的三个凝聚模型(DLA、RLCA和DLCA）13,31之间的联系,故意设定了扩散指数和凝聚概率指数较宽的取值范围.根据Einstein-Stokes定律,γ＞0似乎是很不合理的.但后面的对模拟结果讨论将表明,γ＞0仍然可能有确定的物理意义.扩散指数γ的取值为:2.0,1.0,0.5,0.1,0,-0.5至-3.0(步长为-0.1）;凝聚概率指数σ的取值为:3.0,2.0,1.0,0.5,0.1,0,-0.5至-2.0(步长为-0.1）.

在模拟研究中,随着时间t的延伸,团簇中的粒子数不断增多,团簇的数目不断减少,我们可以对含粒子数s的团簇数Ns(t）进行统计.在三维情形下,设边长为L的立方体点阵中的总粒子数为N0,则粒子密度ρ为N0/L3,对团簇数Ns(t）除以L3进行约化以消除点阵尺寸的影响,得到:

这里的ns(t）是t时刻单位体积内含s个粒子的团簇的数目.研究表明,7,23-25团簇大小分布可用式(5）描述:

式中,t为聚集时间,τ的取值一般介于-2和-2.5之间,文献7已对其取值作了比较详细的研究,根据文献7的研究结果,本文约定τ的取值为-2,S(t）为团簇大小的质量权重平均:

公式(5）中的f(x）为动态标度函数.已有的实验结果7,23-25表明,凝聚过程的早期S(t）随时间t按指数规律增长,即有S(t）～eat,这里a为指数增长因子;而在凝聚过程的后期S(t）随时间t按幂函数规律增长,即S(t）～tb.与前人研究16相同,本模拟实验中对团簇分布的标度关系通过Ns(t）S(t）2对s/S(t）作双对数图来验证,而对团簇大小的质量权重平均随时间的增长关系可以通过对S(t）取对数对t作图和通过S(t）对t作双对数图来观察.

3 结果与讨论

3.1 胶体体系随时间的演变

图1表示了不同γ和σ及其组合作用下胶体体系在凝聚过程中体系团簇总浓度及含有不同粒子数的团簇的浓度随时间的变化关系.图中的蓝虚线代表体系团簇总浓度的变化趋势,另外的5条曲线分别代表了单粒子、2粒子团簇、3粒子团簇、4粒子团簇和5粒子团簇浓度的变化趋势,其它大小团簇浓度的变化趋势与5粒子团簇类似,其曲线没有画出.团簇浓度用体积分数表达,即由体系中这种大小的团簇的总数除以立方体的格点数而得到.体系聚集时间的标度是单粒子在体系中移动单位粒子直径距离所需要的时间.

可以看出,胶体的凝聚过程是团簇总浓度逐渐减小的过程,对于单粒子来说,其浓度都是单调下降,其它团簇的浓度则都是先上升,而后下降,且团簇浓度曲线上都有一最高点.但对于不同的体系(即不同的扩散指数和凝聚概率指数取值）,胶体团簇总浓度及单粒子浓度变化的快慢是不同的,其它团簇浓度曲线的峰高及峰宽也是有较大差异.

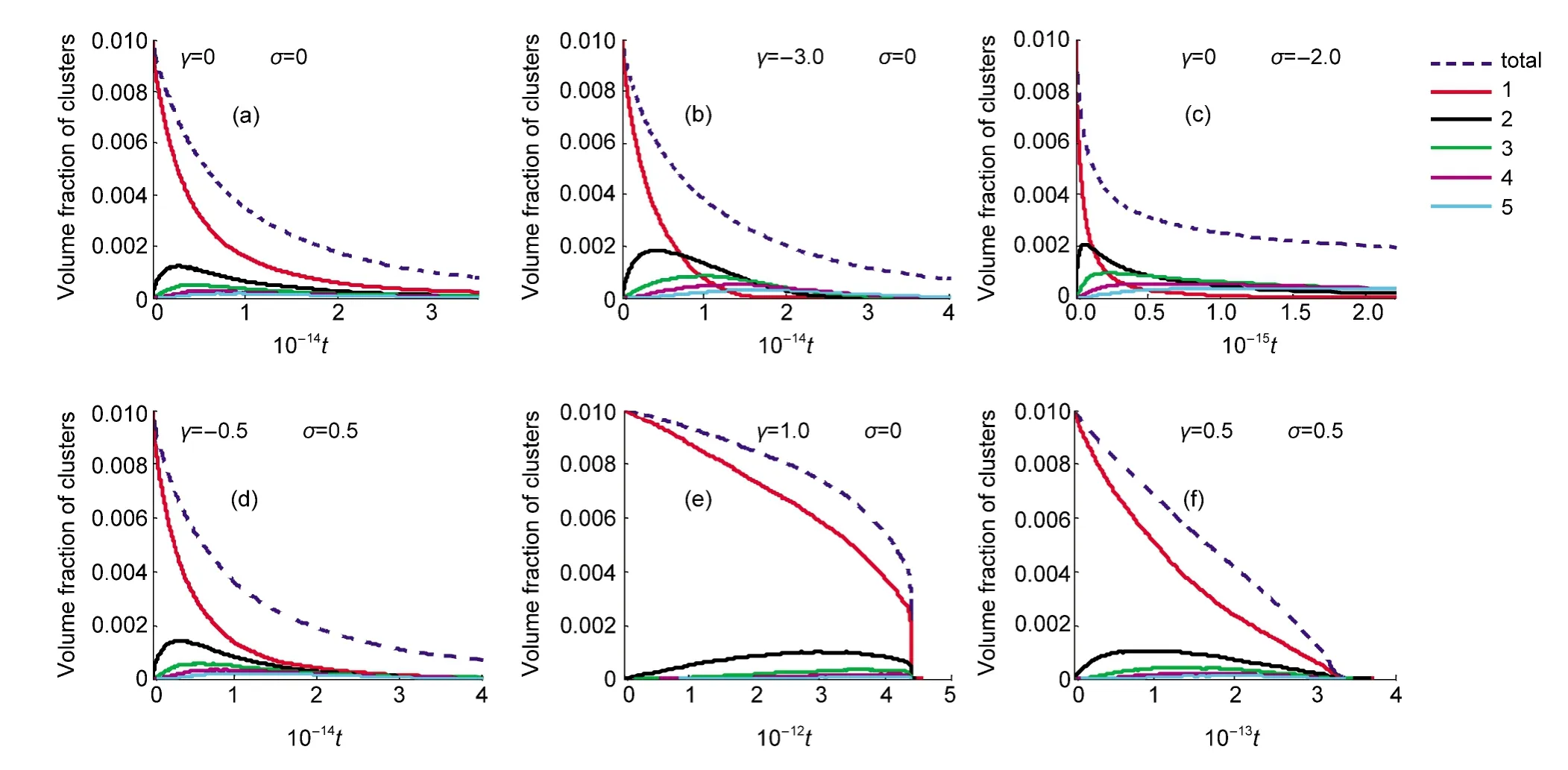
图1 体系的团簇浓度随时间的变化关系Fig.1 Time evolution of concentrations of colloidal clusters in the system

模拟结果表明,在σ取定值的前提下,当γ＜0时,随着γ的增大,峰的高度(团簇的最大浓度）逐渐变低,而峰宽逐渐增大.原因可能是在γ较小的情形中,团簇的扩散系数受团簇大小的影响大,团簇越大,扩散系数越小.在γ=0时,团簇的扩散系数为一常数,这就意味着,大小凝聚体移动的速率相同,浓度变化的速度也就相同.因此,在γ=0时,单粒子浓度下降线不与其它团簇的变化曲线相交,实际上,其它各种团簇浓度变化曲线也是不相交的,即理论上在某一时刻点始终存在各种团簇共存的现象(图1(a））.在γ＜0时,小团簇总会逐渐消失殆尽,大团簇的浓度逐渐增大并超过小团簇的浓度(图1(b））.在γ＞0时,表现出大团簇比小团簇运动快,当γ很大时,则类似于有单一凝聚核的DLA模型(图1(e））.9

图2反映了γ对团簇均匀性的影响.从图2可以看出,γ很小时,形成的团簇非常均匀(图2(a））.当γ很大时,则体系中基本上只有最大的那个团簇在移动,而且这个团簇非常类似于DLA模型形成的产物(图2(b））.该结果表明,γ＞0描述了体系有确定凝聚中心(可能是一个或多个）时的胶体凝聚情形,而当γ＞＞0时,体系只有一个凝聚中心.那么在实际问题中,这种凝聚中心是如何产生的呢?毫无疑问,凝聚中心存在的前提是:大团簇是一个“吸引中心”,即该“吸引中心”对体系中其它小团簇或单粒的吸引力大于小团簇与小团簇、小团簇与单粒及单粒与单粒间的吸引力.在这种情形下,胶体颗粒或小团簇的移动不受布朗运动的制约,而可能是受一种由大团簇产生的作用力场(如强长程范德华力,32电场力等）或体系边界处的外力场的作用.由此可以看出:γ＜0适合于描述颗粒的碰撞概率由布朗运动决定的情况;而γ＞0适合于描述颗粒的碰撞概率由颗粒的“定向移动”决定的情况,而该“定向移动”的推动力可来自于大团簇产生的强“长程范德华力”,“电场力”等,或来自于体系边界处的外力场作用(如重力场33中的沉降过程）.

在γ取定值的前提下,σ对胶体体系的凝聚过程的影响类似于γ对胶体凝聚过程的影响.团簇总浓度随着时间的延长而逐渐降低是必然的趋势,但当σ＜＜0时,后期的凝聚几乎停滞,因此计算机模拟时也很难达到最后形成一个团簇的结果(图1(c））;当σ＞＞0时,则逐渐演变成为快速凝聚,直接受初级粒子有效碰撞概率的影响,即受公式(2）中P0的影响,凝聚过程与图1(a）类似.σ从-2.0变化到3.0的总体趋势是体系向终态(形成一个团簇）发展所需的时间逐渐缩短.但σ增加到一定程度后,体系凝聚成一个团簇的总时间就不会再缩短了,即保持快速凝聚所需的时间.σ具体增加到什么程度而使慢速凝聚变为快速凝聚,依初始粒子的有效碰撞概率P0而定.通过公式(2）可以推算出,当满足σ≥-ln P0/ln(ij）时,大小为i、j的两个团簇碰撞必然发生凝聚;当σ为一固定的正值,i、j满足 ij≥时,体系则由慢速凝聚过渡到快速凝聚.

图2 扩散指数对团簇大小均匀性的影响Fig.2 Effect of diffusivity exponent on clusters′uniformity of size grading

在各种情形中单粒子的浓度都是单调减少的,在σ较小的情况下,大团簇的浓度逐渐超过小团簇的浓度(图1(c））,在σ较大的情况下,小团簇的浓度始终大于大团簇的浓度,与γ的影响相同,最终这两种情况下体系中团簇的浓度都趋向一样,与图1(a）表达的情况类似.与γ不同的是在σ接近-2.0时,峰的高度逐渐变高,峰宽也逐渐增大,在σ趋向0的过程中峰高逐渐变低,峰宽也逐渐减小,到σ＞0后,峰高,峰宽则维持基本不变,这说明在γ=0的情况下,σ在这个范围内对体系团簇的大小分布影响不太明显,因为到凝聚的后期实际上已基本过渡到了快速凝聚阶段,σ的大小只是影响过渡的早晚,σ越大过渡得越快,σ越小过渡得越晚.σ＜0和γ＜0时,随着凝聚过程的发生,体系团簇都体现出均匀分布的特性.σ＜0所对应的均匀性来自于团簇的有效碰撞概率随团簇质量的增大而减小,碰撞主要发生在两个小团簇之间,因此大团簇的继续扩张得到遏制,凝聚过程到后期也就很难继续进行;γ＜0所对应的均匀性来自于单粒或小团簇的移动几率大,从而发生碰撞的可能性也就大,而且这种碰撞主要是因为小团簇的移动造成的,但这并不妨碍大团簇的继续扩张,凝聚过程能继续进行.显然,γ＜0与实际胶体体系在常规情况下的凝聚非常相似,但对σ＜0能否给出合适的物理解释,还期待进一步的研究.

通过大量的γ和σ的组合模拟实验,发现γ对凝聚过程中体系团簇均匀程度的影响占主导作用(图1(d,e,f））,而σ则主要影响团簇的密实程度,这在后边的研究中可以得到证实.根据已有的研究,7,12图1(d）能较好地反映胶体体系在常规情况下的凝聚过程,即体现了小团簇比大团簇移动快,有效碰撞概率随团簇的增大而增大的特性.

3.2 团簇大小分布及其标度关系

图3为体系团簇的大小分布.每个子图中的10条曲线分别代表不同时刻(体系团簇数减少至分别为 0.95N0、0.90N0、0.80N0、0.70N0、0.60N0、0.50N0、0.40 N0、0.30N0、0.20N0、0.10 N0）,粒子数为s的团簇个数Ns(t）对s的双对数关系,其中N0为初始模拟体系的粒子数.这也是Meakin等6从团簇的移动性和Family等7从团簇凝聚概率的角度,单独考察胶粒凝聚过程中团簇大小分布的主要工作.他们认为胶体体系团簇大小分布存在转折点.在主要考虑γ的影响时(令σ=0）,本模拟实验在γ＜-0.7时,团簇大小呈现钟罩形分布,而当γ＞-0.7,团簇分布呈现单调下降;在主要考虑σ的影响时(令γ=0）,当σ＜-0.9时,团簇大小呈现钟罩形分布,而当σ＞-0.9,团簇分布呈现单调下降.图3(a,b）显示了这个转折点时团簇的大小分布,这个转折点的意义在于当γ＞-0.7时或σ＞-0.9时,只要s1＜s2,Ns1(t）恒大于Ns2(t）,即所含粒子数少的团簇的个数始终大于所含粒子数多的团簇的个数,直观表现是团簇分布高度分散.

本模拟实验还探讨了γ和σ的组合影响,以及团簇大小分布曲线的包迹(即各个曲线的公切线）的特征.

模拟实验发现γ和σ对团簇大小分布的组合影响体现一个正负效应的关系,即γ和σ的取值如果都有使团簇大小分布呈现钟罩形分布的趋势,则组合后钟罩形分布的趋势更明显;γ和σ的取值如果都有使团簇大小分布呈单调下降的趋势,则组合后单调下降的趋势更陡,如图3(e）的曲线比图3(f）的曲线更陡;如果γ和σ的取值效应相反,则组合后彼此削弱,对比图3(e）和3(f）,σ=0.5大于转折点(-0.9）,其效应是使团簇分布呈现单调下降,但在图3(f）中γ=-2,其效应是使曲线变得弯曲,由于其值远小于转折点(-0.7）,所以曲线还是呈现了钟罩形.

图3最重要的特征是各时间点团簇大小分布曲线的包迹是一条直线,这说明团簇大小分布有动态标度性质,7,8,12γ和σ组合作用时会对此斜率有一些改变(图3(c,e））,但团簇大小分布曲线的包迹仍然是一条直线,这说明团簇大小分布的标度性质是依然存在的.另外一种考察团簇大小分布是否具有标度性质的方法是通过Ns(t）S(t）2对s/S(t）作双对数图,发现不同时刻体系的团簇分布基本落在同一条标度曲线上(图4）,这说明团簇的大小分布可被动态标度,7,25即各阶段胶体的凝聚过程具有同一性.

3.3 团簇重均大小S(t）的变化

在不同的P0、γ和σ作用下,一般都体现出在凝聚的初始阶段S(t）随t缓慢增加而后迅速增加的规律.这说明胶体的凝聚动力学过程是一个存在正反馈机制的非线性动力学过程.凝聚开始时,体系形成了一些小的团簇,但因小的团簇的范德华力远远大于单粒,所以小的团簇将加速凝聚速度.而凝聚速度的增加使这些小的团簇以更快的速度凝聚成更大的团簇,这反过来又使凝聚速度进一步加快而形成更大的团簇,这种过程可使体系在瞬间迅速完成聚合过程,图5中团簇重均大小S(t）随时间的变化曲线可以清楚地反映出这种正反馈现象.

P0、γ和σ对这种正反馈机制有不同的影响,在γ＜0或σ＞0,当P0取定值时,σ和γ对S(t）的影响并不明显,即对S(t）随t由缓慢增加何时向迅速增加过渡的影响似乎并不明显;相反在γ＞0或σ＜0,当P0取定值时,γ的增大将推动S(t）随t由缓慢增加向迅速增加的过渡,而且这种过渡更迅速,而σ的减小将延迟S(t）随t由缓慢增加向迅速增加的过渡,而且这种过渡也变得缓慢.当σ＜＜0时,凝聚动力学过程就不再是正反馈机制的动力学过程,相反,而变成负反馈机制的动力学过程,由于在这种情况下团簇之间的有效碰撞概率随着团簇质量的增大而减小,所以后期的凝聚过程将变得越来越慢.σ＜＜0可能对应了胶体体系中单粒或团簇之间存在某种排斥力场,而且这种排斥力场随着团簇质量的增大而逐渐增强的现象.

图3 体系团簇的大小分布Fig.3 Cluster-size distribution in the system

在γ和σ取定值时,P0对S(t）随t由缓慢增加何时向迅速增加过渡的影响非常明显,图5表示了γ=-0.5、σ=0.25,P0对这种过渡的影响.从图5中可以看出,随着P0的减小,这种过渡将大大延迟,而且这种过渡也逐渐变得缓慢.从模拟实验看出,P0和σ对S(t）随t变化的影响最为明显.

图4 团簇大小分布时间标度关系Fig.4 Scaling relations of the time-dependent cluster-size distribution

较多的文献讨论了团簇重均大小的标度关系,7,8,12,18,19普遍认为团簇重均大小与体系团簇大小分布的联系可用公式(5）、(6）表达.本模拟实验主要研究了快速凝聚和慢速凝聚情况下团簇重均大小增长规律的联系和区别.图6(a,b）主要表达了在初级粒子有效碰撞概率P0=1的情况下,γ和σ单独作用对团簇重均大小增长规律的影响,其中最右绿色的实线则代表了在P0=0.01、γ=-0.5、σ=0.25时团簇重均大小随时间增长的双对数关系.

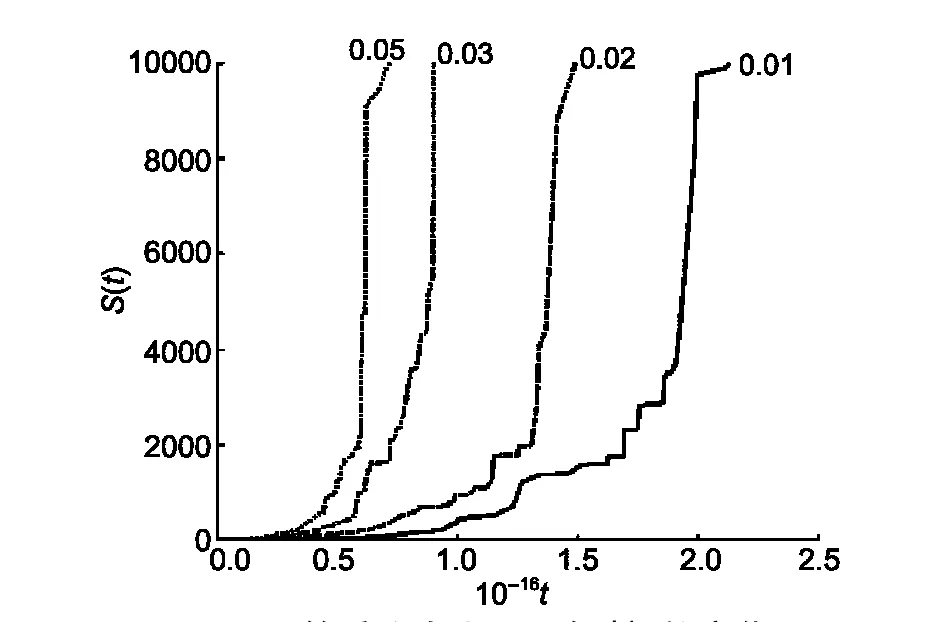
图5 团簇重均大小S(t）随时间的变化Fig.5 Time dependence of the weight-averaged cluster size S(t）

从图6(a）可以看出,在σ=0时,当γ＞0时,随着γ的减少,团簇的平均增长幂函数指数也相应减小,表现为团簇的结构变得疏松,实际上γ＞＞0时,则对应DLA模型.当γ＜0时,各条S(t）随t的增长曲线重合在一起,这说明在扩散控制的凝聚中,粒子的移动与其大小和形状有关,两个粒子一旦相遇即发生凝聚,且一个重要特征是不同体系的凝聚具有同一性,其变化规律是一致的.

从图6(b）可以看出,在γ=0时,当σ＜0时,随着σ的减少,团簇的平均增长幂函数指数也相应减小,表现为团簇的结构变得疏松,实际上σ＜＜0时,则对应慢速凝聚模型.当σ＞0时,团簇间的粘结与其大小和形状有关,团簇间的有效碰撞概率随σ的增大而增大,但到一定程度,实际已发展成为快速凝聚,即有效碰撞概率为1,图6中σ＞0时S(t）的各条增长曲线几乎完全重合在一起的现象正说明了这一点.

关于团簇重均大小随时间增长规律的问题,理论和实际之间还有较大的差距.大多数计算机模拟的结果显示S(t）随t按幂函数规律增长,2,6但实验研究则出现S(t）先随t按指数规律增长,而后按幂函数规律增长的现象.23-25本模拟实验对P0=0.01、γ=-0.5、σ=0.25的情况,早期按对S(t）取对数后对t作图,后期则作S(t）与t的双对数图,观察发现图6(c,d）确实都呈现直线关系,这在一定程度上证实了实验研究的结果,同时也说明本实验使用扩散模型和凝聚模型相结合的方法来模拟胶体体系的凝聚动力学行为是正确的.

图6中P0=0.01、γ=-0.5、σ=0.25的曲线表明,慢速凝聚在初期与快速凝聚有较大的差别,但普通的慢速凝聚进行到一定程度后会发展为快速凝聚,即到后期团簇重均大小的增长规律彼此是一样的.值得注意的是P0=0.01所代表的慢速凝聚与图6(b）中σ＜＜0时所代表的慢速凝聚有本质的区别,这个问题在3.4节有详细的论述.

3.4 扩散指数和凝聚概率指数对团簇分形维数的影响

采用盒维数方法25计算体系团簇的分形维数,如表1所示.每个分形维数对应3次模拟实验,对结果求算术平均,表中除σ=-1.0,-1.5,-2.0外,其它都是最终凝聚形成了一个凝聚体.

在初始条件相同的情况下,当γ＜0时,凝聚体的分形维数基本上是相同的,都为1.93左右,与前面团簇的平均大小S(t）的变化规律是一致的,这也进一步说明不同体系快速凝聚的过程具有同一性.然而,当γ＞＞0,在粒子浓度很低时,团簇凝聚变成与DLA相当,因为在这种情况下实际上只有一个单独的团簇(即最大的团簇）在运动,并且在其扩散运动时,它将余下的单个粒子都收集于自身,表现为分形维数明显增加.

图6 团簇重均大小的标度关系Fig.6 Scaling relations of the weight-averaged cluster size

表1 扩散指数和凝聚概率指数对分形维数的影响Table 1 Effects of diffusivity exponent and stickingprobability exponent on fractal dimension

同样,当σ＞0时,凝聚体的分形维数为1.93左右,与σ=0、γ＜0时的情况非常类似,这时胶体体系过渡到后期实际已完全变成扩散控制凝聚,因为碰撞在一起的两个团簇粘结在一起的概率随着团簇的质量增大而增大,到一定程度有效碰撞概率Pij(σ）实际已等于1,即碰撞就导致粘结,这说明反应控制凝聚(RLCA）会最终过渡到扩散控制凝聚(DLCA）,这也是最终凝聚体分形维数相差不大的根本原因.

σ对团簇分形维数的影响最有趣的结果在于σ＜0的情况.如前文所述,σ＜0对应了慢速凝聚过程,大多文献8,12,13都认为慢速凝聚得到的团簇的分形维数要比快速凝聚的大,但为什么本研究结果得到的分形维数有随着σ的减小而逐渐减小的趋势呢?我们认为其原因在于σ＜0时,碰撞在一起的两个团簇粘结在一起的概率随着团簇的质量增大而减小,在凝聚过程中则体现为两个级别小的团簇更容易粘结在一起,也就是说大团簇的产生是两个小团簇聚结而成的,而不是一个大团簇与一个小团簇聚结而成的(γ＞＞0的情况大多如此）,在这种情况下形成的团簇必然有较小的分形维数.大多文献中所说的慢速凝聚是因为在保持了发生碰撞的两个团簇粘结在一起的概率随着团簇的质量增大而增大的规律的前提下,初级粒子之间的有效碰撞概率P0就很低,在这种情况下,大团簇大多是大团簇与大团簇或大团簇与小团簇聚结而成的,其分形维数必然要比σ＜0时形成的团簇的分形维数大.当σ＜0时,体系成为先快后慢的慢速凝聚,即颗粒越大,有效碰撞概率越小,这可能对应大团簇为一排斥中心,即胶体颗粒存在“排斥力场”的现象.但这只是从凝聚模型得到的一个有趣现象,在什么情况下会存在“排斥中心”?是否有明确的物理意义?还需作进一步的探索.

总之,本研究结果表明,在初级粒子之间的有效碰撞概率就很低的情况下,所谓慢速凝聚从理论上可以分为先慢后快和先快后慢两种情况,先慢后快对应了σ＞0的情况,先快后慢对应了σ＜0的情况.注意,这里提出的先快后慢或先慢后快是对各自的整个凝聚过程而言的,当P0＜＜1时,σ＞0对应的慢速凝聚过程可以用“越来越快”描述其凝聚过程,而σ＜0对应的慢速凝聚过程可以用“越来越慢”表达.

4 结论

Meakin和Family各自独立地考虑团簇的移动性和团簇碰撞的凝聚概率,对胶体体系凝聚过程中团簇大小分布进行了研究,本模拟实验在此基础上,以公式(1）为团簇的移动模型,以公式(2）为团簇的凝聚模型,并将凝聚过程动力学的各个影响因素的作用归结为扩散指数γ和凝聚概率指数σ的作用,系统地考虑团簇的移动性和团簇碰撞的凝聚概率对胶体凝聚动力学行为的影响,得到了如下几个重要结论.

(1）模拟实验证实了在凝聚过程中,早期的团簇重均大小按指数规律增长,而后期按幂函数规律增长的实验现象,这也进一步说明了胶体的凝结动力学过程在常规情况下,是一个存在正反馈机制的非线性动力学过程,而在σ＜＜0时,模拟研究显示该凝聚动力学过程具有负反馈特性,不过该情况是否具有明确的物理意义,目前尚不清楚.

(2）以CCA模型为纽带,考虑γ和σ的作用,将DLCA、RLCA与经典的DLA模型有机地联系在一起:

根据γ,可以将快速凝聚分为DLCA式的快速凝聚和DLA式的快速凝聚.前者对应了无固定凝结核的扩散控制凝聚过程,后者对应了有固定凝结核的扩散控制凝聚过程.已有的研究表明,γ＞0时,前者可逐渐过渡到后者.本文的分析进一步表明,γ＞＞0实际代表了体系中团簇或单粒做“定向运动”而非无规则的布朗运动的情况.这种“定向运动”的推动力可能来自于大团簇产生的强“长程范德华力”,“电场力”等,或来自于体系边界处的外力场的作用.

根据σ,可以将慢速凝聚分为先慢后快,即“越来越快”的慢速凝聚和先快后慢,即“越来越慢”的慢速凝聚.前者对应了P0＜＜1、σ＞0的情况,即常规的胶体凝聚,后者对应了P0＜＜1、σ＜＜0的情况,即可能大团簇为一排斥中心,胶体颗粒存在“排斥力场”的现象;前者为研究慢速凝聚向快速凝聚的过渡提供了依据,后者对胶体的稳定性研究可能有一定的参考价值.

(3）以凝聚模型为基础,对慢速凝聚向快速凝聚的过渡进行了定量描述:当i×j固定,σ≥-ln P0/ln(ij）时,大小为i、j的两个团簇碰撞就要发生凝聚;当σ为一固定的正值,i、j满足ij≥P0-1/σ时,体系则由慢速凝聚过渡到快速凝聚.本研究发现扩散控制凝聚中,不同体系的凝聚具有同一性,其变化规律是一致的.

总之,模拟研究表明,胶体体系的凝聚实际是一种分形凝聚,σ＞0时,其凝聚动力学过程是一个存在正反馈机制的非线性动力学过程,σ＜0时则具有负反馈的特性.显然在进行计算机模拟时必须综合考虑团簇的移动特性和碰撞特性,才能较好地反映胶体凝聚的动力学过程.

(1）Ziff,R.M.;McGrady,E.;Meakin,P.J.Chem.P hys.1985,82(11）,5269.doi:10.1063/1.448600

(2）Rottereau,M.;Gimel,J.C.;Nicolai,T.;Durand,D.Eur.Phys.J.E 2004,15(2）,133.doi:10.1140/epje/i2004-10044-x

(3）Zhang,H.L.;Zhou,G.Journal of Fuel Chemistry and Technology 1998,26(1）,79.[张慧宁,周 革.燃料化学学报,1998,26(1）,79.]

(4）Li,J.S.;Bian X.X.Ch emistry 1998,61(11）,9.[李敬生,边选霞.化学通报,1998,61(11）,9.]

(5）Evilevitch,A.;Rescic,J.;Jönsson,B.;Olsson,U.J.P hys.Chem.B 2002,106(45）,11746.doi:10.1021/jp020467r

(6）Meakin,P.;Vicsek,T.;Family,F.Phys.Rev.B 1985,31(1）,564.doi:10.1103/PhysRevB.31.564

(7）Family,F.;Meakin,P.;Vicsek,T.J.Chem.Phys.1985,83(8）,4144.doi:10.1063/1.449079

(8）Meakin,P.;Family,F.P hys.Rev.A 1988,38(4）,2110.doi:10.1103/PhysRevA.38.2110

(10）Zheng,D.M.;Zhu,S.G.;Jiang,W.T.;Dai,J.Journal of Nanchan g University(E ngineering&Technology）2011,33(2）,129.[郑典模,朱升干,蒋文天,戴 健.南昌大学学报:工科版,2011,33(2）,129.]

(11）Liu,D.J.;Qiu,Z.M.Computers and Applied Chemistry 2012,29(4）,451.[刘东京,邱祖民.计算机与应用化学,2012,29(4）,451.]

(12）Gonzalez,A.E.Phys.Rev.Lett.1993,71(14）,2248.doi:10.1103/PhysRevLett.71.2248

(13）Jullien,R.Conpemp.Ph ys.1987,28(5）,477.doi:10.1080/00107518708213736

(14）Haw,M.;Poon,W.;Pusey,P.P hys.Rev.E 1997,56(2）,1918.doi:10.1103/PhysRevE.56.1918

(15）Meakin,P.;Chen,Z.Y.;Deutch,J.J.Chem.P hys.1985,82(8）,3786.doi:10.1063/1.448890

(16）Meakin,P.J.Sol-Gel Sci.Technol.1999,15(2）,97.doi:10.1023/A:1008731904082

(17）Xiong,H.;Li,H.;Chen,W.;Xu,J.;Wu,L.J.Colloid Interface S ci.2010,344(1）,37.doi:10.1016/j.jcis.2009.12.051

(18）Wang,H.;Pan,Y.M.;Cai,Z.S.;Wang,G.C.;Zhao,X.Z.Chem.J.Chin.Univ.1999,20(9）,1419.[王 惠,潘荫明,蔡遵生,王贵昌,赵学庄.高等学校化学学报,1999,20(9）,1419.]

(19）Wang,H.;Wang,G.C.;Cai,Z.S.;Pan,Y.M.;Zhao,X.Z.Chem.J.Chin.Univ.2000,21(6）,922.[王 惠,王贵昌,蔡遵生,潘荫明,赵学庄.高等学校化学学报,2000,21(6）,922.]

(20）Sandkühler,P.;Lattuada,M.;Wu,H.;Sefcik,J.;Morbidelli,M.Adv.Colloid Interface S ci.2005,113(2）,65.

(21）Klein,R.;Meakin,P.Nature 1989,339(6）,360.

(22）Loh,N.D.;Hampton,C.Y.;Martin,A.V.;et al.Nature 2012,486(7404）,513.doi:10.1038/nature11222

(23）Robinson,D.;Earnshaw,J.Phys.Rev.A 1992,46(4）,2045.doi:10.1103/PhysRevA.46.2045

(24）Robinson,D.;Earnshaw,J.Phys.Rev.A 1992,46(4）,2055.doi:10.1103/PhysRevA.46.2055

(25）Robinson,D.;Earnshaw,J.Phys.Rev.A 1992,46(4）,2065.doi:10.1103/PhysRevA.46.2065

(26）Zhu,H.L.;Li,H.;Jiao,M.Y.;Tian,R.A cta P edolo gica Sinica 2012,49(3）,409.[朱华玲,李 航,贾明云,田 锐.土壤学报,2012,49(3）,409.]

(27）Zhu,H.L.;Li,B.;Xiong,H.L.;Li,H.;Jia,M.Y.A cta Phys.-Chim.Sin.2009,25(6）,1225.[朱华玲,李 兵,熊海灵,李 航,贾明云.物理化学学报,2009,25(6）,1225.]doi:10.3866/PKU.WHXB20090631

(28）Wang,H.X.;Ma,J.;Song,Z.B.;Liu,D.Z.Acta Optica Sinica 2011,31(3）,284.[王红霞,马 进,宋仔标,刘代志.光学学报,2011,31(3）,284.]

(29）Lin,M.;Lindsay,H.;Weitz,D.;Ball,R.;Klein,R.;Meakin,P.Phys.Rev.A 1990,41(4）,2005.doi:10.1103/PhysRevA.41.2005

(30）Lin,M.;Lindsay,H.;Weitz,D.;Klein,R.;Ball,R.;Meakin,P.J.P hys.:Cond es.Matter 1990,2(13）,3093.

(31）Whitesides,G.M.;Grzybowski,B.Science 2002,295(5564）,2418.doi:10.1126/science.1070821

(32）Xiong,H.L.;Yuan,Y.Z.;Li,H.;Zhu,H.L.;Jiang,X.J.A cta Phys.-Chim.Sin.2007,23(8）,1241.[熊海灵,袁勇智,李航,朱华玲,蒋先军.物理化学学报,2007,23(8）,1241.]doi:10.3866/PKU.WHXB20070819

(33）Yuan,Y.Z.;Xiong,H.L.;Li,H.;Zhu,H.L.;Jiang,X.J.A cta Phys.-Chim.Sin.2007,23(5）,688.[袁勇智,熊海灵,李航,朱华玲,蒋先军.物理化学学报,2007,23(5）,688.]doi:10.1016/S1872-1508(07）60044-8