石墨烯条带的电子结构与性质:电场及长度效应
2014-10-18梁万珍
孙 进 梁万珍
(1安徽大学物理与材料科学学院,合肥 230039;2厦门大学化学系,福建厦门 361005)
1 引言
自从单层的石墨也就是石墨烯在实验上被制备出来以后,1-3人们不断发现这是一种具有有趣的物理特性以及显著应用前景的纳米材料.目前,石墨烯以及以石墨烯为基础的其它结构的材料已引起人们广泛的关注和研究,例如,s-p磁性的早期发现,纳米尺度石墨烯在技术上的开发,以及表面修饰、外场、压力对于石墨烯性质的影响等等.4-13石墨烯的可控性为人们制备出高效率、低成本的电磁分子器件提供了一条可能的途径.
如果将单层的石墨烯沿着一些特殊的线剪开,就可以得到具有准一维结构的石墨烯纳米带(GNR).石墨烯纳米带材料与碳纳米管有着天然的联系.沿着周期性方向,按照带的两边不同的形状,石墨烯纳米带也可以分为椅子型(armchair)和锯齿型(zigzag)两种不同的类型.不同的边带形状或不同的长度都可能会影响石墨烯纳米带的电子和磁性质.我们可以通过研究纳米带材料来增加对纳米管的认识,同时,在纳米管的研究中,一些已经比较完备的实验手段也可以在纳米带材料上得到充分应用.最近,这种在10 nm以下尺寸的石墨烯纳米带也的确可以由化学方法获得.14相应的在这个尺度上纳米带的物理化学性质研究必将会有更大的发展.
加州大学伯克利分校的Louie研究组15利用密度泛函理论和紧束缚近似研究了armchair型和zigzag型纳米带材料的电子结构.研究显示,两种结构的石墨烯纳米带都是半导体性质.而zigzag型由于边界态在费米能级附近,会通过自旋极化来降低体系的能量,导致磁性的产生,引起了更广泛的研究,包括它的自旋性质、磁性、半金属性等等.16-21
由于石墨烯特殊的电导率,22它的光学及激发态性质一直是人们关注的一个焦点.理论上,通过对激发态上光学性质的研究,单、双层以及其它类型的石墨烯的光学电导率相继被计算出来,23-27从而有效地促进了石墨烯材料作为分子器件的应用与发展.我们知道具有n个重复单元的zigzag型石墨烯纳米带(n-ZGNR)的基态具有半导体性质,如果它的周期性重复单元的个数n<32的话,那么它的反铁磁态的能量会总是小于铁磁态的能量.因而在这种情况下,基态上n-ZGNR两个边上的电子自旋方向相反,具有反铁磁性.17,20但是,目前还很少有文章报道过石墨烯纳米带在激发态上,不同自旋方向电子的不同之处,以及它们对于激发态和光学等性质的影响.Lu等28曾经对较短的石墨烯纳米带进行过计算,他们利用极化子模型,比较了不同自旋的自旋波函数,并且研究了不同自旋的电荷响应动力学过程.此外,Zhao等29则在平均场近似下,研究了以石墨烯作为分子器件在输运过程中不同的自旋电流.
本文我们选择了体系较小的zigzag型石墨烯条带分子,利用密度泛函理论(DFT)计算了其基态的电子结构,并在此基础上采用实时的含时密度泛函理论(TDDFT)方法,对超短激光脉冲影响下实时的电子动力学性质进行了研究.避免线性展开,求解完整的含时密度泛函方程或含时Hartree-Fock方程的方法,可以直接用来研究在不同的外激光脉冲影响下的电子动力学过程以及多光子激发.因而这种方法目前被广泛地用于强场过程的研究.30-33对于石墨烯条带分子,深入研究它们在超短激光脉冲影响下的电子动力学过程有助于其在分子器件方面的应用与发展,因而是必须和迫切的.
本文采用密度泛函及含时密度泛函方法讨论了宽度上包含8个zigzag链的石墨烯条带基态及激发态的性质,包括条带长度、静电场对于石墨烯条带磁性的影响以及激发态上随着激光脉冲的变化,自旋向上和自旋向下的电子的不同表现.
2 计算方法
在含时密度泛函理论框架下,第i个分子轨道波函数Ψi满足含时薛定谔方程

其中υext(r)和υxc[]ρ(r)分别是外势和交换相关势.等式(1)可以写成密度矩阵形式的含时密度泛函方程,也就是标准的Liuviolle方程

其中F(t)和ρ(t)分别为Fock矩阵和密度矩阵.对于等式(3)的求解,可以在微扰理论基础上分别对Fock矩阵和密度矩阵进行展开,从而得到线性和非线性的性质.
目前,含时密度泛函理论已经成功地被应用于线性光学性质的计算.但是对于一些超短的强激光脉冲过程,非线性性质非常显著,如果采用线性响应的方法则无法体现出来.为了充分考虑系统与外电场之间的非线性相互作用,本文中,我们避免使用微扰展开理论,而是求解完整的含时密度泛函方程,从而使得在求解的过程中能够平等地对待外电场和原子或分子之间的库仑力.含时密度泛函方程和含时Hartree-Fock方程一样是一个微分方程,因而可以用一些标准的数值计算方法进行求解.但是低阶的Verlet和Runge-Kutta数值方法34都需要非常小的时间步长来确保密度矩阵的厄米性.除此以外,在每一个时间步长里,Fock矩阵都要被构造很多次,这是非常耗时的.为了提高整个计算的效率,我们充分利用厄米变换,并采用改进的中间点计算方法.35考虑到随着时间步长的推进,密度和外场的线性变化,通过对时间步长中间点的Fock矩阵的计算来演化密度矩阵.这种方法能够非常有效地处理求解含时的密度泛函方程过程中对于时间演化算符的积分.我们已经用此方法成功计算过碳纳米管等纳米材料的光学及动力学性质.36-39具体来看,在含时密度泛函理论中,时间演化过程可概括如下:

在此过程中,首先利用ti时间点的Fock矩阵F(ti)按照公式(4,5)将密度矩阵从ρ(ti-1/2)演化到ρ(ti+1/2),然后用同样的方法按照公式(6,7)可以得到ti+1时间点的密度矩阵ρ(ti+1)和Fock矩阵F(ti+1),从而为下一个时间步长的计算做准备.由于在演化过程中,矩阵U和U'都是厄米矩阵,在每一个时间步长中,矩阵的等幂性都能够得到保证.此外,由于在每一个时间步长中,只需要构造一次Fock矩阵,因而计算速度得到了很大的提高.对于演化过程中矩阵的幂指数计算,我们用Taylor展开进行处理.

在过去的研究中我们发现,当展开阶数k=100时,计算结果就能够保持稳定.36在研究过程中,由于希望能够观察到石墨烯条带分子在激发态上的动力学过程,因而加入一个极化的强激光脉冲,

其中F、ω、τ和t分别指外激光场的强度、频率、脉冲持续宽度及时间.
3 计算结果及讨论
本文选择了长度较短的,仅仅包含了8个zigzag链(8-ZGNR)的zigzag型石墨烯纳米条带,其化学式为C168H36.由于长度较短,C168H36在有些方面表现得更像一个分子,但是作为zigzag型石墨烯纳米条带的单元分子,也能够反映出纳米条带的部分性质.我们在DFT/TDDFT的理论框架下,采用B3LYP杂化泛函,对C168H36的基态和激发态的性质进行研究.由于要进行实时的TDDFT计算,考虑到计算量的问题,采用小基组STO-3G,对应要处理876个轨道基函数.这一基组在我们之前的研究工作40中也采用过,并且得到了较好的结果.对于C168H36分子的结构在UB3LYP/STO-3G的量子化学理论水平上进行了优化,得到的分子结构如图1所示.分子在同一平面上,C―C键的长度为0.144 nm左右,C―H键的长度为0.110 nm.所有的密度泛函及含时密度泛函计算都是在Q-Chem商业软件包41发展版本的框架下进行的.
3.1 基态电子密度

图1 8-ZGNR分子结构Fig.1 Geometry of 8-ZGNR
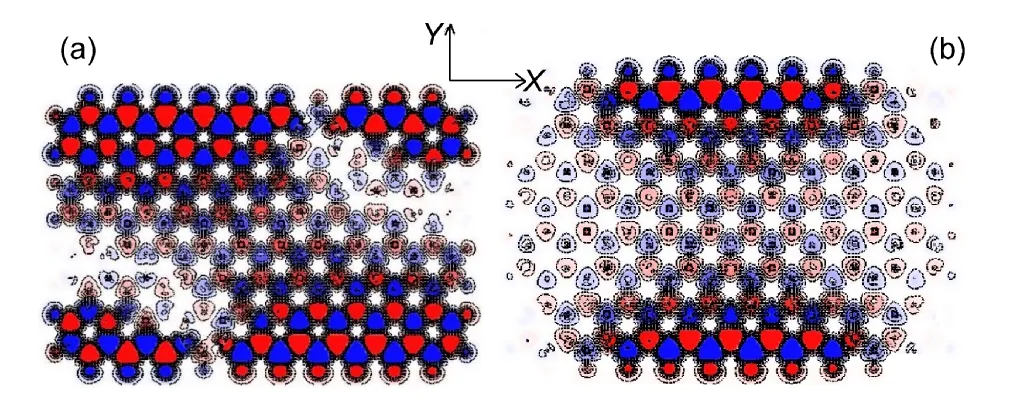
图2 (a)C168H36的基态自旋密度;(b)在基态模拟中加入了一个静电场(沿Y方向)情况下的自旋电子密度Fig.2 (a)Spin density of C168H36in ground state;(b)spin density of C168H36where a static field(along the Y direction)is added in the simulation
首先,我们研究了有限长石墨烯纳米条带C168H36的基态性质.在UB3LYP/STO-3G的计算水平上,对C168H36分子模型进行了自旋非限制的自洽计算,图2为计算出的自旋密度(ρα(r)-ρβ(r)).根据以往的研究,对于zigzag型石墨烯纳米条带,自旋电子密度在其两边的自旋方向是相反的,因而zigzag型石墨烯纳米条带具有反铁磁性的基态性质.但是在我们的计算中,对于C168H36分子,它的基态自旋电子密度并没有显示出反铁磁的性质(图2(a)).尽管在相邻的C原子之间自旋密度交替变换,但是在分子两边带上的电子自旋方向并不是完全相反的,在有一些地方,电子自旋还是平行的.这与Hod等20的计算结果不同,我们认为这首先是由于B3LYP杂化泛函所起的关键作用,类似于B3LYP泛函可以影响到对于石墨烯纳米带的半金属性质的计算结果.19其次,在我们的研究中,当石墨烯纳米条带分子的长度较短时,如C168H36,它更像是一个分子,而不能体现出石墨烯纳米带反铁磁性的基态性质.为了证明长度的影响,我们又计算了C328H56的基态自旋电子密度(图3),它的长度是C168H36的两倍.图3的计算结果非常清楚地显示,α自旋和β自旋的电子密度在相邻的C原子间交替出现,而在石墨烯条带分子的两边电子密度的自旋方向是反平行的,这说明随着长度的增加,石墨烯纳米条带会显示出反铁磁的基态特性.本文中我们也考虑了加入一个垂直于石墨烯的一维方向,强度为0.01 a.u的静电场的情况.结果表明对于C168H36,静电场会大大改变它基态的性质.首先,静电场会改变电子的自旋方向.图2(b)是加入静电场后,自旋电子密度的计算结果.对于C168H36,静电场使得自旋电子密度往中间集中,并且两边带上的电子自旋呈现出反平行的特性.其次,也对最高占据分子轨道(HOMO)与最低非占据分子轨道(LUMO)之间的带隙进行了分析.在不加静电场时,对于α自旋和β自旋电子带隙是相等的,为1.17 eV.但是加入静电场后,α自旋和β自旋电子显示出了不同的性质,α自旋的带隙会稍微增大,为1.22 eV,而β自旋的带隙则会明显减小,为0.52 eV.对于这一部分的计算,也用稍大的基组3-21G进行了验证.发现基组的增加虽然可以大大降低基态的能量,但是对于外场的作用并没有本质的影响.在零外场时得到的不同自旋能量带隙是相同的,为0.76 eV,当电场强度达到0.01 a.u时,α自旋的带隙增大,为1.06 eV,而β自旋的带隙会减小,为0.46 eV.通过比较足以表明,STO-3G基组对于加入横向外场后不同自旋态的计算结果是合理的.Louie等16曾经报道过,如果将石墨烯纳米带放入一个静电场中,它的α自旋和β自旋电子的HOMO-LUMO带隙会发生不同的变化.α自旋态的能量带隙会增大,而β自旋态的则会减小,从而显示出半金属的特性.我们的计算结果也确实证明了这一变化过程,与之前的报道16也是符合的.

图3 C328H56的基态自旋电子密度Fig.3 Spin density of C328H56in ground sate
在加入横向电场后,α自旋和β自旋的不同表现主要是由于外电场对于不同的自旋态有着相反的影响.它会使得α自旋和β自旋电子分别朝着不同的方向重新排布,并且使得β自旋态的占据轨道和非占据轨道在能量上更加靠近,而α自旋态则分离得更远.为了更好地观察α自旋和β自旋电子对于外电场的作用所显示出的不同表现,在下一部分对激发态性质的计算中,我们一直沿用了在基态计算时加入这样一个静电场的计算结果.
3.2 激光场诱导的电子密度
对于8-ZGNR激发态性质的研究,考虑了在外激光场的作用下,诱导电子密度随时间的演化.在对C168H36基态的计算时,为了保持基态的反铁磁性质,我们仍然保留一个强度为0.01 a.u.的静电场.而在基态计算的基础上,对激发态的计算模拟中,则另加入了一个随时间变化的激光脉冲.如图4所示,在时间域中,8-ZGNR经历了两个激光脉冲,模拟的总时间为1600 a.u.,时间步长为0.4 a.u.通过对等式(3)的计算,可以在时间域中计算出诱导电子密度δρ(t)=ρ(t)-ρ(0).由此可以得到诱导电子密度,即为某一时刻t和初始时刻的电子密度之差.

图4 外激光场脉冲随时间的变化Fig.4 External laser field changes with time

在上式中,φλ代表第λ个原子轨道.图5和图6分别为计算得到的在一个激光脉冲中不同的四个时间点上α自旋和β自旋诱导电子密度随时间的变化.随着外激光场的不同,首先不论是α自旋还是β自旋诱导电子密度都会随时间发生明显的变化并且诱导电子会随着外场的方向而发生移动;但是对于不同的自旋,有着不同的变化特点.如图5(a)所示,对于α自旋,当t=240.8 a.u.时,外激光场的强度接近其正向最大值(图4中的a点),此时产生了较强的诱导电子密度,特别是在石墨烯纳米带的上下边缘上.沿着外激光场的方向,正负诱导电子密度发生分离,相邻C原子上的电子密度极性相反.当t=384.8 a.u.时,此时外激光场强度很小,接近于零(图4中的b点).受此影响,α自旋诱导电子密度也变得很弱,几乎消失不见(图5(b)).当t=480.8 a.u.时,外激光场接近于其负最大值(图4中的c点),图5(c)显示出诱导电子密度又增强很多,且多集中在石墨烯分子的边缘.但是对比图5(a)发现,此时诱导电子密度的正负正好相反.这说明诱导电子会沿着外激光场的方向移动,当外场的极化方向由正向转为反向时,诱导电子的极性也会反向.最后,当t=768.8 a.u.时,外激光场又一次接近于零(图4中的d点),此时诱导电子密度除了在zigzag边的中间部分,其它地方也几乎消失不见(图5(d)).
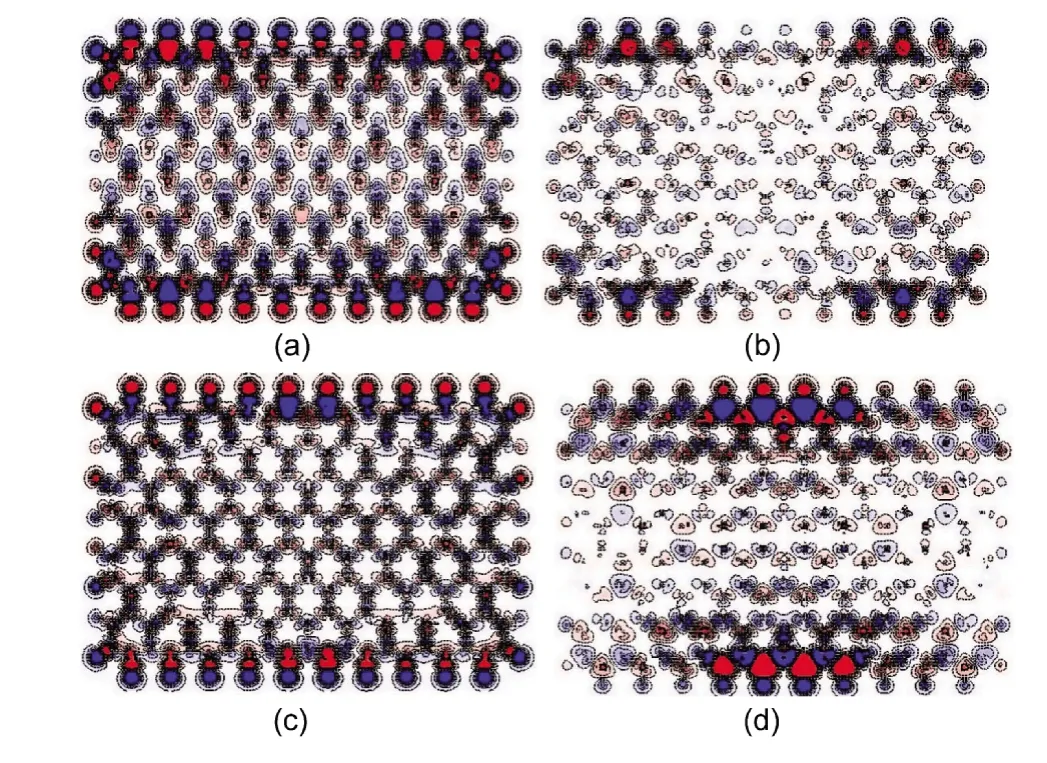
图5 在外激光场的作用下C168H36的α自旋诱导电子密度Fig.5 Induced α-spin charge density of C168H36interacting with an external laser field

图6 在外激光场的作用下C168H36的β自旋诱导电子密度Fig.6 Induced β-spin charge density of C168H36interacting with an external laser field
对于β自旋,图6显示出诱导电子密度随着外激光场变化与α自旋共同的特点,如β自旋诱导电子会沿着外激光场的极化方向而发生移动,会随着外激光场强度的变化而增强或减弱.但是对比图5(a)和图6(a),发现在同样强度的外激光场的影响下,产生的β自旋诱导电子密度要比α自旋弱很多.同样的情况在t为384.8和480.8 a.u.时刻也会出现.但是当t=768.8 a.u.时,虽然外激光场的强度已接近于零,但是β自旋诱导电子密度并没有出现明显的减弱.从诱导偶极矩随时间的变化(图7)发现,在t=768.8 a.u.时刻,诱导偶极矩出现了非常明显的非绝热效应.而图6(d)更是证明了这一点,此时的β自旋诱导电子密度已经并不完全受外激光场的影响,非绝热效应使得即使外场的强度接近于零,诱导电子密度的强度也不会发生明显的减弱.而同样的情况之所以没有出现在图4(d)所示的α自旋诱导电子密度中,则说明了β自旋比α自旋电子态更容易出现非绝热效应.

图7 诱导偶极矩随时间的变化Fig.7 Induced dipole moment changes with time
4 结论
在密度泛函和含时密度泛函理论的基础上,对于含有8个zigzag链长度较短的石墨烯纳米条带C168H36的基态和激发态的性质进行了研究.发现在基态上,B3LYP杂化泛函的计算结果显示较短的石墨烯纳米条带并不能表现出反铁磁性质,但是随着长度的增加,纳米条带上两边的自旋密度会出现反平行,从而显示出反铁磁的基态性质.静电场的加入,会降低石墨烯纳米条带C168H36的反铁磁态的能量,成为能量最稳定的基态.同时,静电场也会使得α自旋和β自旋的HOMO-LUMO的带隙大小出现不同的变化,其中α自旋带隙的大小基本不变,而β自旋带隙则明显变小.这一计算结果也证明了zigzag型石墨烯纳米带的半金属特性.
在激发态上,加入了一个随时间变化的激光脉冲,通过在时间域里求解含时密度泛函方程,从而观察石墨烯纳米条带C168H36在激发态上的动力学过程.研究发现,随着外激光脉冲的变化,诱导电子密度会随着外场强度的增强或减弱而相应地增大或减少,并且会随着外场的极化方向而发生明显移动.此外,α自旋和β自旋电子在激发态上的动力学过程仍然会有不同的表现.相比而言,在同样强度的外激光场的影响下,α自旋电子更容易被激发而产生较明显的诱导电子密度,而β自旋电子则更容易脱离外激光场的控制而产生非绝热现象.
(1)Novoselov,K.S.;Geim,A.K.;Morozov,S.V.;Jiang,D.;Zhang,Y.;Dubonos,S.V.;Grigorieva,I.V.;Firsov,A.A.Science 2004,306,666.doi:10.1126/science.1102896
(2)Novoselov,K.S.;Geim,A.K.;Morozov,S.V.;Jiang,D.;Katsnelson,M.I.;Grigorieva,I.V.;Dubonos,S.V.;Firsov,A.A.Nature 2005,438,197.doi:10.1038/nature04233
(3)Zhang,Y.;Tan,Y.W.;Stormer,H.L.;Kim,P.Nature 2005,438,201.doi:10.1038/nature04235
(4)Novoselov,K.S.;Jiang,D.;Schedin,F.;Booth,T.J.;Khotkevich,V.V.;Morozov,S.V.;Geim,A.K.Proc.Natl.A cad.Sci.U.S.A.2005,102,10451.doi:10.1073/pnas.0502848102
(5)Novoselov,K.S.;Jiang,Z.;Zhang,Y.;Morozov,S.V.;Stormer,H.L.;Zeitler,U.;Maan,J.C.;Boebinger,G.S.;Kim,P.;Geim,A.K.Science 2007,315,1379.doi:10.1126/science.1137201
(6)Zhang,Y.;Small,J.P.;Pontius,W.V.;Kim,P.Appl.P hys.L ett.2005,86,073104.doi:10.1063/1.1862334
(7)Berger,C.;Song,Z.;Li,T.;Li,X.;Ogbazghi,A.Y.;Feng,R.;Dai,Z,;Marchenkov,A.N.;Conrad,E.H.;First,P.N.;de Heer,W.A.J.Phys.Ch em.B 2004,108,19912.doi:10.1021/jp040650f
(8)Peres,N.M.R.;Guinea,F.;Castro Neto,A.H.Phys.R ev.B 2006,73,125411.doi:10.1103/PhysRevB.73.125411
(9)Kane,C.L.;Mele,E.J.Phys.Rev.Lett.2005,95,226801.doi:10.1103/PhysRevLett.95.226801
(10)Pereira,V.M.;Guinea,F.;Lopes dos Santos,J.M.B.;Peres,N.M.R.;Castro Neto,A.H.Phys.Rev.Lett.2006,96,036801.doi:10.1103/PhysRevLett.96.036801
(11)Sun,D.L.;Peng,S.L.;Ouyang,J.;Ouyang,F.P.Acta Phys.-Chim.Sin.2011,27,1103.[孙大立,彭盛霖,欧阳俊,欧阳方平.物理化学学报,2011,27,1103.]doi:10.3866/PKU.WHXB20110345
(12)Li,Y.X.;Wei,Z.D.;Zhao,Q.L.;Ding,W.;Zhang,Q.;Chen,S.G.Acta Phys.-Chim.Sin.2010,26,1570.[李云霞,魏子栋,赵巧玲,丁 炜,张 骞,陈四国.物理化学学报,2010,26,1570.]doi:10.3866/PKU.WHXB20100620
(13)Hu,Y.J.;Jin,J.;Zhang,H.;Wu,P.;Cai,C.X.A cta Phys.-Chim.Sin.2010,26,2073.[胡耀娟,金 娟,张 卉,吴 萍,蔡称心.物理化学学报,2010,26,2073.]doi:10.3866/PKU.WHXB20100812
(14)Yang,X.;Dou,X.;Rouhanipour,A.;Zhi,L.;Räder,H.J.;Müllen,K.J.Am.Ch em.Soc.2008,130,4216.doi:10.1021/ja710234t
(15)Son,Y.;Cohen,M.L.;Louie,S.G.P hys.R ev.L ett.2006,97,216803.doi:10.1103/PhysRevLett.97.216803
(16)Son,Y.W.;Cohen,M.L.;Louie,S.G.Nature 2006,444,347.doi:10.1038/nature05180
(17)Jiang,D.;Sumpter,B.G.;Dai,S.J.Chem.P hys.2007,127,124703.doi:10.1063/1.2770722
(18)Hod,O.;Barone,V.;Peralta,J.E.;Scuseria,G.E.Nano Lett.2007,7,2295.doi:10.1021/nl0708922
(19)Rudberg,E.;Selek,P.;Luo,Y.Nano L ett.2007,7,2211.doi:10.1021/nl070593c
(20)Hod,O.;Barone,V.;Scuseria,G.E.Phys.Rev.B 2008,77,035411.doi:10.1103/PhysRevB.77.035411
(21)Xu,B.;Yin,J.;Xia,Y.D.;Wan,X.G.;Jiang,K.;Liu,Z.G.Appl.P hys.Lett.2010,96,163102.doi:10.1063/1.3402762
(23)Zhang,C.;Chen,L.;Ma,Z.Phys.Rev.B 2008,77,241402.doi:10.1103/PhysRevB.77.241402
(24)Stauber,T.;Peres,N.M.R.;Geim,A.K.Ph ys.Rev.B 2008,78,085432.doi:10.1103/PhysRevB.78.085432
(25)Cserti,J.;Csordas,A.;David,G.Phys.Rev.Lett.2007,99,066802.doi:10.1103/PhysRevLett.99.066802
(26)Wright,A.R.;Liu,F.;Zhang,C.Nanotechnology 2009,20,405203.
(27)Liu,J.;Wright,A.R.;Zhang,C.;Ma,Z.A ppl.Ph ys.Lett.2008,93,041106.doi:10.1063/1.2964093
(28)Lu,J.Q.;Zhang,X.G.;Pantelides,S.T.Phys.Rev.B 2009,79,073408.doi:10.1103/PhysRevB.79.073408
(29)Zhao,Z.Y.;Zhai,X.C.;Jin,G.J.Appl.Phys.L ett.2012,101,083117.doi:10.1063/1.4748110
(30)Zhang,G.P.P hys.Rev.L ett.2005,95,047401.doi:10.1103/PhysRevLett.95.047401
(31)Gordon,A.;Kartner,F.X;Rohringer,N.;Santra,R.Ph ys.Rev.Lett.2006,96,223902.doi:10.1103/PhysRevLett.96.223902
(32)Onida,G.;Reining,L.;Rubio,A.Rev.Mod.P hys.2002,74,601.doi:10.1103/RevModPhys.74.601
(33)Suzuki,M.;Mukamel,S.J.Chem.Phys.2003,119,4722.doi:10.1063/1.1594721
(34)Press,W.H.;Teukolsky,S.A.;Vetterling,W.T.;Flannery,B.P.Numerical Recipes in Fortran 90;Cambridge University Press:Cambridge,1996.
(35)Li,X.;Smith,S.M.;Markevitch,A.N.;Romanov,D.A.;Levis,R.J.;Schlegel,H.B.Phys.Chem.Ch em.Phys.2005,7,233.doi:10.1039/b415849k
(36)Sun,J.;Song,J.;Zhao,Y.;Liang,W.Z.J.Ch em.Phys.2007,127,234107.doi:10.1063/1.2805396
(37)Sun,J.;Guo,Z.Y.;Liang,W.Z.Ph ys.Rev.B 2007,75,195438.doi:10.1103/PhysRevB.75.195438
(38)Sun,J.;Liang,W.Z.;Liu,J.J.T h eo.Comp.Chem.2008,7,579.doi:10.1142/S0219633608003976
(39)Sun,J.;Liu,J.;Liang,W.Z.;Zhao,Y.J.Ph ys.Chem.A 2008,112,10442.doi:10.1021/jp804408a
(40)Sun,J.;Liang,W.Z.;Yang,J.L.;Gao,J.S.J.Mol.S truct.-Theochem 2005,755,105.doi:10.1016/j.theochem.2005.07.030
(41)Shao,Y.;Molnar,L.F.;Jung,Y.;Kussmann,J.;Ochsenfeld,C.;Brown,S.T.;Gilbert,A.T.B.;Slipchenko,L.V.;Levchenko,S.V.;O′Neill,D.P.;DiStasio,R.A.;Lochan,R.C.;Wang,T.;Beran,G.J.O.;Besley,N.A.;Herbert,J.M.;Lin,C.Y.;Van Voorhis,T.;Chien,S.H.;Sodt,A.;Steele,R.P.;Rassolov,V.A.;Maslen,P.E.;Korambath,P.P.;Adamson,R.D.;Austin,B.;Baker,J.;Byrd,E.F.C.;Dachsel,H.;Doerksen,R.J.;Dreuw,A.;Dunietz,B.D.;Dutoi,A.D.;Furlani,T.R.;Gwaltney,S.R.;Heyden,A.;Hirata,S.;Hsu,C.P.;Kedziora,G.;Khalliulin,R.Z.;Klunzinger,P.;Lee,A.M.;Lee,M.S.;Liang,W.;Lotan,I.;Nair,N.;Peters,B.;Proynov,E.I.;Pieniazek,P.A.;Rhee,Y.M.;Ritchie,J.;Rosta,E.;Sherrill,C.D.;Simmonett,A.C.;Subotnik,J.E.;Woodcock,H.L.;Zhang,W.;Bell,A.T.;Chakraborty,A.K.,Chipman,D.M.;Keil,F.J.;Warshel,A.;Hehre,W.J.;Schaefer,H.F.;Kong,J.;Krylov,A.I.;Gill,P.M.W.;Head-Gordon,M.Phys.Ch em.Chem.Phys.2006,8,3172.doi:10.1039/b517914a
