硫族铅化物阳离子低电子态的理论研究
2014-10-18曹战利王治钒杨明理
曹战利 王治钒 杨明理 王 繁,*
(1四川大学原子与分子物理研究所,成都 610065;2四川大学化学学院,成都 610065)
1 引言
硫族铅化物具有很多独特的物理性质,如对称的能带结构,强烈依赖于温度的窄带隙,重空穴带的缺失,1另外,硫族铅化物量子点的电子和空穴有相对较大的玻尔半径,即使在较大的尺寸下仍然能表现出较强的量子限制效应.2这些特性使得它们在中红外激光器和探测器制造、红外线和可见光辐射、激光二极管、光伏电池、药物诊断、工业过程监控、大气污染控制等诸多方面有重要应用.3此外,包含IV-VI族元素的材料也可以用于量子限制效应设备,2所以硫族铅化物PbS、PbSe、PbTe一直以来都是人们的研究热点.4-6目前针对硫族铅化物的理论研究主要集中在相应团簇的结构和激发态性质.团簇是连接微观粒子和宏观粒子的媒介,而许多原子团簇在生长中会有不同的结构形状变化,所以对它们的结构和性能研究就显得尤为重要,不少作者对硫族元素和第II、IV族元素形成的团簇已经展开研究,7-13这些研究反映了由不同元素参与形成团簇的不同生长模式.但是对硫族铅化物分子及离子开展的研究则比较少,而研究硫族铅化物分子及其离子的基态和低激发态性质将有助于理解硫族铅化物团簇的结构以及光学性质.14-19本文中,我们将研究PbS、PbSe、PbTe阳离子的基态和低激发态的性质.
对于硫族铅化物,由于涉及到重元素,必须考虑相对论效应才能得到可靠的结果.目前量子化学中处理相对论效应最流行的方法是相对论有效势(RECP)方法.20,21该方法用有效势来代替内层电子对外层电子的作用,并通过适当选取有效势中的参数来计算相对论效应.由于不用直接考虑内层电子,基函数数目和所要处理的电子数都大大减少,因此使用有效势可以显著降低计算量.相对论效应分为标量相对论效应和旋轨耦合效应,不考虑旋轨耦合效应时常用的相对论有效势与非相对论有效势在数学形式上完全一致,因此计算起来非常简单.如果要考虑旋轨耦合效应,计算量就会明显增加.虽然旋轨耦合对闭壳层分子的一阶能量校正贡献为零,但是对6p区元素而言,即使闭壳层性质分子旋轨耦合效应可能仍然比较显著,而且本文所关注的PbS、PbSe、PbTe阳离子都是开壳层分子,因此要可靠描述这些阳离子的基态和低激发态性质就必须考虑旋轨耦合效应.对于硫族铅化物分子及阳离子,Balasubramanian22首先用含旋轨耦合的相对论组态相互作用(RCI)方法计算了PbS+的2Π1/2态和2Π3/2态的键长和频率.Wang等23在全活性空间自洽场方法(CASSCF)基础上用多参考态组态相互作用(MRSDCI)方法计算了PbSe和PbTe的基态以及相应阳离子的基态和低激发态的光谱常数,他们对这些态的谐振频率得到的结果与实验值吻合较好,但是他们得到的中性分子平衡键长比实验值偏大约0.005 nm左右,而阳离子平衡键长则比实验值偏大约0.01 nm.对键长的误差可能与他们计算中所选取的有效势和基组有关.Jalbout等24则采用密度泛函理论计算了硫族铅化物分子及阴离子的键长和频率.
耦合簇(CC)方法25,26自从上世纪六十年代以来被广泛用于研究原子分子中的电子相关效应,该方法具有大小一致性,并且对电子的动态相关能有很高的计算精度,是目前最流行的计算电子相关效应的量子化学方法之一.其中CCSD(T)方法27也是目前精度最高的常用单参考态方法.本文中,采用我们组最近发展的含旋轨耦合的运动方程耦合簇计算电离能(EOMIP-CC)方法28,29研究PbS、PbSe、PbTe阳离子的基态和低激发态的性质.在EOMIP-CC方法中,首先用CC方法计算比目标态多一个电子的参考态的能量和波函数,再通过EOMIP方法计算目标态的能量和波函数.在计算旋轨耦合方面,我们在求解参考态Hartree-Fock方程时没有考虑旋轨耦合,而只在求解CC方程和EOMIP方程时考虑旋轨耦合.因此在计算中所用轨道为实自旋轨道,与在自洽场计算时就考虑旋轨耦合的方法相比,计算效率更高.由于CC方法的单激发算符能很好地描述轨道弛豫,此前的计算结果30,31显示,这个方法即使对于超重元素分子也能精确地描述旋轨耦合效应.此外,在EOMIP方法中,如果参考态为闭壳层体系,这个方法得到的体系波函数能完全避免自旋污染,这一特点对于描述旋轨耦合尤其重要,因为使用不是自旋纯态的波函数计算旋轨耦合效应会导致本非相互作用的态之间由于旋轨耦合而相互耦合,从而造成能级的错误分裂.目前常用的EOMIP-CC方法都是基于CCSD级别,这个方法适用于主要从参考态电离一个电子而不激发另一个电子所得到的状态.在耦合簇方法中,要得到高精度的计算结果往往需要考虑三重激发的贡献.直接基于CCSDT的方法计算量很大,一般只适用于很小的体系和基组.采用微扰法考虑三重激发贡献的EOMIP-CC方法能提高EOMIP-CCSD方法的计算精度,32,33但是这些方法尚未在含旋轨耦合的EOMIP-CC方法上实现.
在本文中,我们分别采用含旋轨耦合和不含旋轨耦合的EOMIP-CCSD方法计算PbS+、PbSe+、PbTe+基态和低激发态的光谱常数以及这些态所对应的垂直电离能和绝热电离能,并考察旋轨耦合效应对所研究体系的这些性质的影响.此外,在不考虑旋轨耦合的情况下,还将用CCSD和CCSD(T)方法直接计算这些体系的性质,通过与EOMIP-CCSD方法的计算结果的对比,考察三重激发对所研究性质的影响.
2 基本理论和计算细节
在耦合簇理论中,CCSD方法34的激发算符由单激发和双激发耦合簇算符所组成,其总能量为:

其中耦合簇算符T1和T2的定义如下:

上式中ϕ0为标量相对论下的HF行列式波函数,H为含旋轨耦合的哈密顿量,i,j,k,…(a,b,c,…)代表波函数ϕ0中的占据(空)轨道,算符ai表示当其作用于ϕ0时,从占据轨道φi上湮灭一个电子,而则表示在空轨道φa上生成一个电子,和分别表示耦合簇算符T1和T2的系数,其中T1和T2所满足的方程为:

旋轨耦合效应通常对于开壳层体系比对闭壳层体系更加显著.对于不存在空间简并的开壳层态如Σ态,可以直接采用我们所发展的用于计算闭壳层体系的含旋轨耦合耦合簇方法加以研究.但是对于空间简并的态如Π态或者Δ态,从实自旋轨道构建的行列式波函数出发求解含旋轨耦合的CC方程时常常会出现难以收敛的情况.为了计算考虑旋轨耦合情况下开壳层分子的性质,我们在闭壳层体系的含旋轨耦合的耦合簇理论基础上实现了运动方程耦合簇方法(EOM-CC)38计算电离能的办法,即EOMIP-SOC-CCSD方法,28该方法适用于比闭壳层体系少一个电子的开壳层体系.在EOMIP-CCSD方法中,基态波函数取为R eTϕ0,其中R为电离算符:
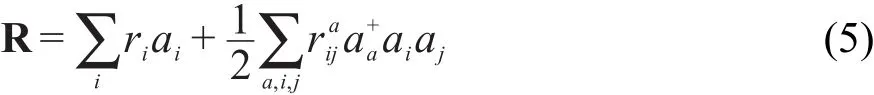
ri和为EOMIP-CCSD中的r振幅,此时电离态的能量可由下式得到:


其中Eip就是电离能.考虑旋轨耦合后,r振幅则会为复数,我们通过利用时间反演对称性来降低计算量.如果波函数选为R eTϕ0,则它的时间反演态为R′eTϕ0=KR eTϕ0,其中K为时间反演算符.容易证明电离算符R和R′中的r振幅满足如下关系式:

基态硫族铅化物中性分子价电子的电子组态为1σ22σ23σ21π4,39其中3σ轨道是由两个原子的pz轨道组合而成的成键轨道,1π轨道是由两个原子的px和py轨道分别组合而成的成键轨道.本文中所研究的PbS+、PbSe+、PbTe+电子态为分别从3σ轨道和1π轨道上电离一个电子所得到的2Σ+态和2Π态.如果考虑旋轨耦合效应,2Σ+态变成2态,2Π态则会分裂成2Π1/2和2Π3/2,而且2Σ1/2态和2Π1/2由于具有相同的对称性还会进一步相互耦合.通过选择硫族铅化物中性分子的基态为参考态,用EOMIP-CC方法即可得到PbS+、PbSe+、PbTe+的2Σ+态和2Π态或者2Σ1/2,2Π1/2以及2Π3/2态的能量和性质.在计算过程中,Pb的内层1s到4f轨道上的60个电子对其它电子的作用使用有效势替代,在计算中只考虑5s25p65d106s26p2电子,而Te的内层1s到3d轨道上的28个电子对其它电子的作用使用有效势替代,在计算中只考虑4s24p64d105s25p4电子.对于Pb和Te,分别采用Stugart/Kohn组发展的含旋轨耦合的ECP60MDF和ECP28MDF有效势,40,41其他原子则采用全电子计算.计算过程中所选用的基函数为与相应有效势匹配且考虑了旋轨耦合影响的Def2-QZVPP-2C基函数.42不考虑旋轨耦合时,这些体系的2Σ+态和2Π态为相应对称性下的能量最低态,所以可以直接用UCCSD和UCCSD(T)方法进行计算.另外,我们还采用不含旋轨耦合的EOMIP-CCSD方法计算了2Σ+态和2Π态,通过与UCCSD(T)方法的结果比较可以考察EOMIP-CCSD方法的精度以及三重激发的影响.
在本文当中,基于CFOUR程序包,43用CCSD、CCSD(T)、SOCCSD、SOCCSD(T)方法计算了 PbS,PbSe和PbTe分子1Σ+态的键长和频率,用UCCSD、UCCSD(T)以及EOMIP-CCSD方法计算了PbS+、PbSe+、PbTe+阳离子2Σ+态和2Π态的键长和频率,用EOMIPSOC-CCSD方法计算了PbS+、PbSe+和PbTe+阳离子下2、2Π1/2、2Π3/2态的键长和频率,另外,还计算了这些态所对应的垂直电离能和绝热电离能.
3 计算结果与讨论
分别采用含旋轨耦合和不含旋轨耦合的CCSD以及CCSD(T)方法得到的PbS、PbSe和PbTe平衡键长和谐振频率计算结果列在表1中,相应的实验数据44以及此前的理论计算结果23,24也列在这个表中.计算中性分子的主要目的是考察我们所用的RECP以及相应的基函数的精度.由表1的结果可以看出,无论是否考虑旋轨耦合效应,CCSD得到的键长比CCSD(T)的计算结果要短约0.002 nm,而频率要比CCSD(T)得到的频率大.此外,旋轨耦合效应使这三个分子的谐振频率都略有降低,但是对于PbS和PbSe的键长几乎没有影响,而对于PbTe,在CCSD和CCSD(T)级别上旋轨耦合效应使键长分别增长了0.0004和0.0007 nm,这显示PbTe中的旋轨耦合效应更加显著.从表1还可以看到,考虑旋轨耦合效应后CCSD(T)的结果与实验值吻合非常好,键长与实验键长的差别小于0.0004 nm,而频率则仅比实验值偏大1-3 cm-1.我们所得到的结果明显好于此前文献中基于组态相互作用或者密度泛函理论得到的结果.这些结果表明本文中所使用的RECP和基函数所引起的误差非常小.
采用 UCCSD、UCCSD(T)、EOMIP-CCSD 方法计算所得到的不含旋轨耦合时PbS+,PbSe+和PbTe+2Σ+态和2Π态的键长和频率结果列在表2中,这些方法得到的PbS、PbSe和PbTe的垂直电离能和绝热电离能结果列在表3中.比较表1和表2的结果可以看到,对于硫族铅化物,从3σ轨道或者1π轨道上电离一个电子后体系的键长增长,谐振频率降低.这是由于3σ轨道和1π轨道都是成键轨道,从这些轨道上电离一个电子后会削弱化学键所导致的.从表2还可以看到,2Π态的键长比2Σ+态的键长长约0.014 nm,振动频率也比2Σ+态频率略小.对比UCCSD和UCCSD(T)的结果显示三重激发对阳离子的影响小于对中性分子的影响:三重激发使这些阳离子态的键长增长约0.0003-0.0010 nm,而频率减小约5-8 cm-1.EOMIP-CCSD方法得到的这些阳离子态的键长比UCCSD的结果小0.001 nm,而频率则略大.EOMIP-CCSD方法的结果与UCCSD(T)的结果差别也列在表2中,作为EOMIP-CCSD方法中三重激发对这些阳离子电子态键长和频率影响的估计值.以UCCSD(T)的结果为标准可以看到,EOMIP-CCSD方法给出的键长和频率误差比UCCSD方法的误差更大.从表3的结果可以看出,虽然2Π态的键长比2Σ+态的键长长,但是2Π态的能量比2Σ+态的能量更低.此外,对比UCCSD和UCCSD(T)的结果可以看到三重激发使电离能增加,这与三重激发对中性分子的影响比对阳离子的影响更显著是一致的:相比于阳离子,三重激发使中性分子的能量降低更多.EOMIP-CCSD得到的电离能则略高于UCCSD(T)的结果,这是由于EOMIP-CCSD方法对参考态的描述通常好于对电离态的描述,从而得到的电离能偏大所引起的.从这个表还可以看到,UCCSD得到的电离能结果比UCCSD(T)得到的电离能结果小约0.1-0.2 eV,而EOMIP-CCSD方法得到的电离能则与UCCSD(T)方法的结果吻合更好,差别都在0.04 eV以内.这些结果显示虽然EOMIP-CCSD方法对这些态的平衡键长和谐振频率的误差比UCCSD大,但是EOMIP-CCSD得到的电离能结果有较高的精度.
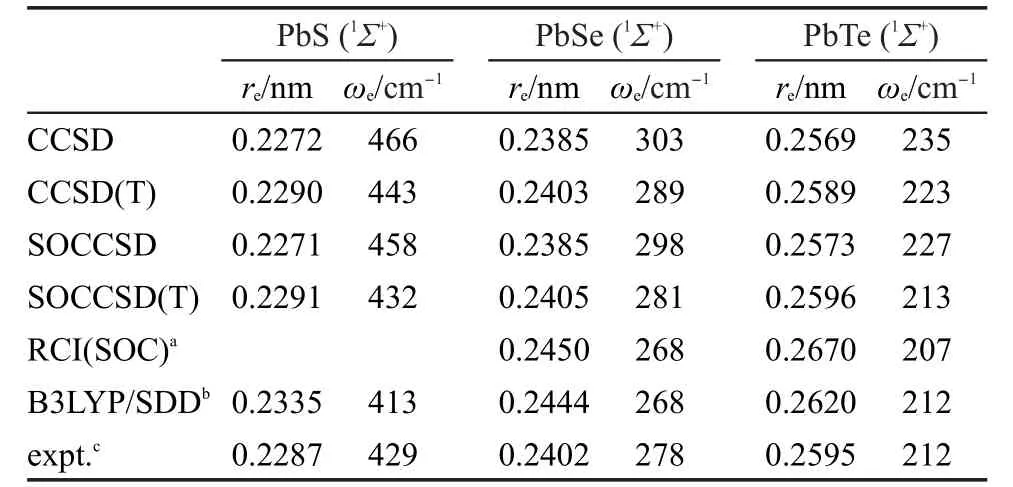
表1 PbS,PbSe和PbTe基态的键长和频率Table 1 Bond lengths and frequencies for ground states of PbS,PbSe,and PbTe

表2 不考虑旋轨耦合时PbS+、PbSe+和PbTe+的键长和频率Table 2 Bond lengths and frequencies of PbS+,PbSe+,and PbTe+without spin-orbit coupling

表3 不考虑旋轨耦合时PbS,PbSe和PbTe的电离能Table 3 Ionization energies of PbS,PbSe,and PbTe without spin-orbit coupling
用EOMIP-SOC-CCSD方法计算得到的含旋轨耦合情况下PbS+、PbSe+、PbTe+的2Σ1/2,2Π1/2和2Π3/2态的键长和频率结果列在表4中,PbS、PbSe、PbTe的垂直电离能和绝热电离能结果列在表5中.文献中采用含旋轨耦合的CI方法计算结果22,23以及已有的实验数据23也列在这两个表中.为了考察旋轨耦合的影响,不含旋轨耦合的EOMIP-CCSD方法的计算结果也列在这两个表中作为比较.对于2Π态,旋轨耦合使之分裂为2Π1/2和2Π3/2态.从表4的结果可以看到,PbS+和PbSe+的2Π3/2态键长和相应的2Π态键长几乎相等而频率则略低,这两个离子的2Π1/2态键长比相应的2Π3/2态或2Π态键长短约0.0015 nm,而频率比2Π3/2态频率反而更低.对于PbTe+,2Π1/2和2Π3/2态的键长和频率几乎相等且键长比2Π态长约0.001 nm,频率低约10 cm-1.与不含旋轨耦合时的2Σ+态相比,旋轨耦合效应使PbS+和PbSe+的2Σ1/2态键长增长约0.003 nm,频率反而分别变大20和10 cm-1,对于PbTe+,旋轨耦合使2Σ1/2态的键长只增加0.0004 nm,频率减小4 cm-1.从这些结果可以看到,虽然Te的核电荷数大于S和Se,但是对于2Σ1/2和2Π1/2态,旋轨耦合效应对PbS+和PbSe+的影响明显强于PbTe+;而对于2Π3/2态,PbTe+中的旋轨耦合效应才强于PbS+和PbSe+.这主要是由于在PbS+和PbSe+中2Σ1/2和2Π1/2态之间由于自旋轨道相互作用的耦合强于PbTe+中这两个态之间的相互耦合所引起的.从EOMIP-SOCCCSD得到的r振幅可以看到,PbS+和PbSe+的2Σ1/2态波函数中所包含的2Π1/2态成分分别约为15%和14%,而PbTe+的2Σ1/2态波函数中不明显包含2Π1/2态的成分,而PbS+和PbSe+的2Π1/2态波函数中所包含的2Σ1/2态成分约为 8%,同样,PbTe+的2Π1/2态波函数中不明显包含2Σ1/2态的成分.从中性分子的轨道能量看,PbS和PbSe中3σ轨道比1π轨道能量分别低0.223和0.367 eV,而PbTe分子中,3σ轨道比1σ轨道能量低0.551 eV.此外,从表3中也可以看到,PbS、PbSe和PbTe中2Σ+态与2Π态的能量差分别为0.34、0.41和0.47 eV,这些都与PbS+和PbSe+中2Σ1/2和2Π1/2态之间的耦合强于PbTe+中这两个态之间的耦合相一致.由于2Σ+态的键长比2Π态的键长短,因此这两个态之间的混合导致2Σ1/2态的键长比2Σ+态的键长长,而2Π1/2态的键长则比2Π1/2态的键长短.从表4中可以看到,EOMIP-SOC-CCSD得到的结果比此前用含旋轨耦合的CI方法得到的结果与实验值吻合更好,特别是我们得到的PbSe+的2Π3/2态键长比2Π1/2态键长长,这与实验结果在定性上是一致的,而含旋轨耦合的CI方法得到相反的结果.与实验结果相比,EOMIP-SOC-CCSD方法得到的键长偏短而频率偏大,如果考虑三重激发的校正,我们得到的结果会与实验值吻合更好.

表4 考虑旋轨耦合时PbS+,PbSe+和PbTe+的键长和频率Table 4 Bond lengths and frequencies of PbS+,PbSe+,and PbTe+with spin-orbit coupling
从表5的结果可以看到,这些硫族铅化物阳离子的基态为2Π3/2态,而2Π1/2态能量比2Π3/2态能量高,这与他们的电子组态为π3相一致.对比含旋轨耦合和不含旋轨耦合的垂直电离能,我们可以看到,PbS和PbSe的2Π3/2态电离能与2Π态电离能差别不大,而2Π1/2态只比2Π3/2态能量高 0.03 eV 左右,而对于PbTe,2Π3/2态垂直电离能明显低于2Π态电离能,而2Π1/2态比2Π3/2态能量高 0.6 eV.对于2Σ1/2态,PbS 和PbSe的垂直电离能比2Σ+态高0.25 eV左右,而PbTe的2Σ1/2态垂直电离能比2Σ+态高0.18 eV左右.PbS+和PbSe+中2Π1/2态和2Π3/2态能量分裂明显小于PbTe+中的分裂,而与2Σ+态相比,PbS+和 PbSe+中2Σ1/2态能量的升高也比PbTe+中2Σ1/2态能量升高得更加显著,这都是与2Π1/2和2Σ1/2态之间的混合有关:2Π1/2和2Σ1/2态之间的耦合导致2Π1/2能量降低而2Σ1/2态能量升高,在PbS+和 PbSe+中2Π1/2和2Σ1/2态耦合明显而PbTe+中这两个态基本没有混合.为了进一步阐明这些阳离子中2Π态的能量分裂以及2Π1/2和2Σ1/2态之间的耦合,我们仿照惰性气体双原子分子阳离子的旋轨耦合矩阵,45引入如下能量矩阵描述旋轨耦合相互作用:

表5 考虑旋轨耦合时PbS,PbSe和PbTe的电离能Table 5 Ionization energies of PbS,PbSe,and PbTewith spin-orbit coupling

其中E(2Σ+)和 E(2Π)分别表示2Σ+态和2Π态的能量,c表示旋轨耦合引起的体系整体能量的变化,a表示2Π态的能量分裂,d表示2Π1/2和2Σ1/2态之间的耦合.我们用2Σ+态和2Π态对应的垂直电离能代替2Σ+态和2Π态的能量,这个能量矩阵的本征值表示2Σ1/2、2Π1/2和2Π3/2态对应的垂直电离量,可以得到式(10)中的参数:对于PbS+有a=0.199 eV,d=0.274 eV,c=0.084 eV,对于PbSe+有a=0.212 eV,d=0.286 eV,c=0.081 eV,对于PbTe+有a=0.671 eV,d=0.144 eV,c=0.100 eV.从这些结果可以看到,PbTe+中2Π态的能量分裂明显大于PbS+和PbSe+中的2Π态能量分裂,而PbTe+中2Π1/2和2Σ1/2态之间的耦合很弱不仅仅是因为PbTe+中2Σ+态和2Π态的能量差别较大,PbTe+中2Π1/2和2Σ1/2态之间的旋轨耦合矩阵元也只是PbS+和PbSe+中的一半.与实验的电离能结果相比,除了PbSe的2Π1/2态绝热电离能比实验值小0.25 eV外,我们的结果与实验值差别都在0.2 eV以内.
4 结论
研究了PbS+、PbSe+、PbTe+阳离子的基态2Π态和第一激发2Σ+态的能量和性质.由于包含6p区原子,因此旋轨耦合效应会对这两个电子态有很明显的影响.在考虑旋轨耦合后,2Π态会分裂为2Π3/2和2Π1/2态,而2Σ+态会变成2Σ1/2态,而且2Π1/2态和2Σ1/2态还会进一步相互混合.采用我们最近发展的含旋轨耦合的运动方程耦合簇计算电离能的方法,在CCSD级别上研究了PbS、PbSe、PbTe阳离子在这些电子态下的键长和频率以及这些态所对应的垂直和绝热电离能,得到的结果与已有的实验值吻合较好.在不考虑旋轨耦合的情况下,这些阳离子的2Σ+态和2Π态可以直接用高精度的CCSD(T)进行计算,通过比较EOMIP-CCSD与CCSD(T)的结果,考察了三重激发对计算结果的影响,结果显示考虑三重激发的贡献后得到的键长和频率结果与实验值吻合更好.还通过比较含旋轨耦合以及不含旋轨耦合的计算结果,考察了旋轨耦合效应对这几个离子电子态的影响.在这几个阳离子中,PbTe+中2Π态的能量分裂明显大于PbS+和PbSe+中2Π态的能量分裂,但是PbTe+中2Π1/2和2Σ1/2态之间的相互耦合则明显弱于PbS+和PbSe+中这两个态之间的耦合.PbTe+中2Π1/2和2Σ1/2态之间耦合很弱一方面是因为2Σ+态和2Π态的能量差别比PbS+和PbSe+中2Σ+态和2Π态的能量差别大,另一方面还由于PbTe+中2Π1/2和2Σ1/2态之间的旋轨耦合矩阵元只是PbS+和PbSe+中2Π1/2和2Σ1/2态之间的旋轨耦合矩阵元的一半.这些计算结果为PbS+、PbSe+、PbTe+阳离子的这些电子态的性质提供了新的理论数据,可以为将来的实验数据作为参考.
(1)Cao,C.F.;Wu,H.Z.;Si,J.X.;Xu,T.N.;Chen,J.;Shen,W.Z.Acta Phys.Sin.2006,55,2021.[曹春芳,吴惠桢,斯剑霄,徐天宁,陈 静,沈文忠.物理学报,2006,55,2021.]
(2)Lipovskii,A.;Kolobkova,E.;Petrikov,V.;Kang,I.;Olkhovets,A.;Krauss,T.;Thomas,M.;Silcox,J.;Wise,F.;Shen,Q.Appl.Phys.Lett.1997,71,3406.doi:10.1063/1.120349
(3)Feit,Z.;McDonald,M.;Woods,R.;Archambault,V.;Mak,P.Appl.Phys.Lett.1996,68,738.doi:10.1063/1.116726
(4)Krauss,T.D.;Wise,F.W.;Tanner,D.B.Phys.Rev.Lett.1996,76,1376.doi:10.1103/PhysRevLett.76.1376
(5)Schwarzl,T.;Heib,W.;Springholz,G.Appl.Phys.Lett.1999,75,1246.doi:10.1063/1.124656
(6)Giuliano,B.M.;Bizzocchi,L.;Cooke,S.;Banser,D.;Hess,M.;Fritzsche,J.;Grabow,J.U.Phys.Chem.Chem.Phys.2008,10,2078.doi:10.1039/b716896a
(7)Troparevsky,M.C.;Chelikowsky,J.R.J.Chem.Phys.2001,114,943.doi:10.1063/1.1329126
(8)Karamanis,P.;Maroulis,G.;Pouchan,C.J.Chem.Phys.2006,124,071101.doi:10.1063/1.2173236
(9)Wang,J.;Ma,L.;Zhao,J.;Jackson,K.A.J.Chem.Phys.2009,130,214307.doi:10.1063/1.3147519
(10)Sanville,E.;Burnin,A.;BelBruno,J.J.J.Phys.Chem.A 2006,110,2378.doi:10.1021/jp056218v
(11)Zeng,H.;Schelly,Z.A.;Ueno-Noto,K.;Marynick,D.S.J.Phys.Chem.A 2005,109,1616.doi:10.1021/jp040457l
(12)He,J.;Liu,C.;Li,F.;Sa,R.;Wu,K.Chem.Phys.Lett.2008,457,163.doi:10.1016/j.cplett.2008.03.085
(13)Koirala,P.;Kiran,B.;Kandalam,A.K.;Fancher,C.A.;de Clercq,H.L.;Li,X.;Bowen,K.H.J.Chem.Phys.2011,135,134311.doi:10.1063/1.3635406
(14)Zeng,Q.;Shi,J.;Jiang,G.;Yang,M.;Wang,F.;Chen,J.J.Chem.Phys.2013,139,094305.doi:10.1063/1.4819695
(15)Hummer,K.;Grüneis,A.;Kresse,G.Phys.Rev.B 2007,75,195211.doi:10.1103/PhysRevB.75.195211
(16)Albanesi,E.A.;Okoye,C.;Rodriguez,C.M.I.;Blanca,E.L.P.Y.;Petukhov,A.G.Phys.Rev.B 2000,61,16589.doi:10.1103/PhysRevB.61.16589
(17)Bartnik,A.;Efros,A.L.;Koh,W.K.;Murray,C.;Wise,F.Phys.Rev.B 2010,82,195313.doi:10.1103/PhysRevB.82.195313
(18)Isborn,C.M.;Kilina,S.V.;Li,X.;Prezhdo,O.V.J.Phys.Chem.C 2008,112,18291.doi:10.1021/jp807283j
(19)Kamisaka,H.;Kilina,S.V.;Yamashita,K.;Prezhdo,O.V.J.Phys.Chem.C 2008,112,7800.doi:10.1021/jp710435q
(20)Dolg,M.;Cao,X.Chem.Rev.2011,112,403.
(22)Balasubramanian,K.J.Phys.Chem.1984,88,5759.doi:10.1021/j150667a059
(23)Wang,L.S.;Niu,B.;Lee,Y.T.;Shirley,D.;Balasubramanian,K.J.Chem.Phys.1990,92,899.doi:10.1063/1.458124
(24)Jalbout,A.F.;Li,X.H.;Abou-Rachid,H.Int.J.Quantum Chem.2007,107,522.
(25)Gauss,J.Encyclopedia of Computational Chemistry;Schleyer,P.V.R.,Allinger,N.L.,Clark,T.,Gasteiger,J.,Kollmann,P.A.,Schaefer,H.F.,Schreiner,P.R.,Eds.;Wiley and Sons:New York,1998;p 615.
(26)Bartlett,R.J.;MusiaB,M.Rev.Mod.Phys.2007,79,291.doi:10.1103/RevModPhys.79.291
(27)Raghavachari,K.;Trucks,G.W.;Pople,J.A.;Head-Gordon,M.Chem.Phys.Lett.1989,157,479.doi:10.1016/S0009-2614(89)87395-6
(28)Tu,Z.;Wang,F.;Li,X.J.Chem.Phys.2012,136,174102.doi:10.1063/1.4704894
(29)Stanton,J.F.;Gauss,J.J.Chem.Phys.1994,101,8938.doi:10.1063/1.468022
(30)Wang,F.;Gauss,J.;van Wüllen,C.J.Chem.Phys.2008,129,064113.doi:10.1063/1.2968136
(31)Kim,I.;Park,Y.C.;Kim,H.;Lee,Y.S.Chem.Phys.2012,395,115.doi:10.1016/j.chemphys.2011.05.002
(32)Stanton,J.F.;Gauss,J.J.Chem.Phys.1999,111,8785.doi:10.1063/1.479673
(33)Manohar,P.U.;Stanton,J.F.;Krylov,A.I.J.Chem.Phys.2009,131,114112.doi:10.1063/1.3231133
(34)Purvis,G.D.,III;Bartlett,R.J.J.Chem.Phys.1982,76,1910.doi:10.1063/1.443164
(35)Tu,Z.;Yang,D.D.;Wang,F.;Guo,J.J.Chem.Phys.2011,135,034115.doi:10.1063/1.3611052
(36)Wang,F.;Gauss,J.J.Chem.Phys.2008,129,174110.doi:10.1063/1.3000010
(37)Wang,F.;Gauss,J.J.Chem.Phys.2009,131,164113.doi:10.1063/1.3245954
(38)Stanton,J.F.;Bartlett,R.J.J.Chem.Phys.1993,98,7029.doi:10.1063/1.464746
(39)Yang,C.Y.;Rabii,S.J.Chem.Phys.1978,69,2497.doi:10.1063/1.436891
(40)Peterson,K.A.;Figgen,D.;Goll,E.;Stoll,H.;Dolg,M.J.Chem.Phys.2003,119,11113.doi:10.1063/1.1622924
(41)Metz,B.;Stoll,H.;Dolg,M.J.Chem.Phys.2000,113,2563.doi:10.1063/1.1305880
(42)Armbruster,M.K.;Klopper,W.;Weigend,F.Phys.Chem.Chem.Phys.2006,8,4862.doi:10.1039/b610211e
(43)Stanton,J.F.;Gauss,J.;Harding,M.E.;Szalay,P.G.with contributions from Auer,A.A.;Bartlett,R.J.;Benedikt,U.;Berger,C.;Bernholdt,D.E.;Bomble,Y.J.;Cheng,L.;Christiansen,O.;Heckert,M.;Heun,O.;Huber,C.;Jagau,T.C.;Jonsson,D.;Jusélius,J.;Klein,K.;Lauderdale,W.J.;Matthews,D.A.;Metzroth,T.;Mück,L.A.;O’Neill,D.P.;Price,D.R.;Prochnow,E.;Puzzarini,C.;Ruud,K.;Schiffmann,F.;Schwalbach,W.;Stopkowicz,S.;Tajti,A.;Vázquez,J.;Wang,F.;Watts,J.D.and the integral packages MOLECULE(Almlöf,J.;Taylor,P.R.),PROPS(Taylor,P.R.),ABACUS(Helgaker,T.;Jensen,H.J.A.;Jørgensen,P.;Olsen,J.),and ECP routines by Mitin,A.V.;van Wüllen,C.,CFOUR,Version1.2;For the current version,see http://www.cfour.de.
(44)Huber,K.P.;Herzberg,G.Spectroscopic Constants of Diatomics,1st ed.;Van Nostrand Reinhold Company:New York,1979;pp 528-530.
(45)Liang,Y.N.;Wang,F.;Guo,J.J.Chem.Phys.2013,138,094319.doi:10.1063/1.4792435
