探究几种不等式的证明方法在数学中的应用

2014-10-17翟金成

河南科技 2014年19期

翟金成

（郑州幼儿师范高等专科学校，河南郑州 450000）

不等式是高等数学研究中的重要工具，证明不等式也是高等数学中的常见题型。针对不等式证明的方法较多，而对不等式证明方法的系统研究较少。本文将对不等式证明的具体方法进行阐述，并就几种常见的证明方法进行探讨，以扩展学生的解题思维，提升学生的创新思维能力。

1 利用微分学方法来解题

在微分学方法的探讨与应用中，常用的方法有函数的单调性、函数的极限、函数的凹凸性，以及微分中值定理等，现就其应用及约束条件进行阐述。

1.1 利用函数的单调性来解题

函数的单调性是最常见的证明不等式的方法之一，其方法主要有：在证明不等式 f（x）＞g（x）时，通常需要对之进行变形操作，使之转变为 f（x）-g（x）＞0 或，或者引入构造函数 F，由此得出F（x）在区间上的单调性。例如：当 x＞0 时，求证。对于该题在证明过程中，首先设定，当 F（0）=0 时，得出 F’（x），再由 F’（x）来判定在相应区间内函数的单调性，进而证明不等式F（x）成立。在对本例题进行归纳时，需要从两个方面来考虑，一是将不等式进行作差转化；二是当作差不成立时可以做商处理，并利用函数的单调性来推导出不等式成立。

1.2 利用函数的极限法来求证

当构造函数在给定区间不单调，或是遇到 f（x）≥a或 f（x）≤b（a，b为常数）类型的不等式时，可以利用极限法来求解。例如：当 p＞1，试求证对于任意 x∈[0，1]都有不等式（1-x）p≤1 成立。从上题可知，对于函数 f（x）=xp+（1-x）p，可以从导数运算中得出在区间[0，1]中的最大值为1，最小值为从而得出不等式成立。

1.3 利用函数的凹凸性来求证

凹凸性是函数性质之一，涉及同一函数在不同点处的函数值时，往往利用函数的凹凸性来证明。例如：对于某三角形ΔABC的三个内角 A、B、C来说，试求证 sinA+sinB+sinC≤在求证该不等式成立时，需要先构造凹函数f（x）=-sinx。当 f（x）=-sinx，0＜x＜π，则有 f″（x）=sinx＞0。根据函数的凹凸性，很容易得出不等式成立。

1.4 利用拉格朗日中值定理来求证

对含有增量的不等式进行求证时，可以对函数进行变形。当函数 f（x）在[a，b]区间可以生成增量 f（b）-f（a）或者时，则满足拉格朗日中值定理。例如：求证当x＞0时，不等式＜ln（1+x）＜x 成立。在证明过程中，首先借助构造函数得出 f（t）=lnt，当 f（t）满足[1，1+x]（x＞0）时，利用拉格朗日中值定理得出不等式成立。

2 利用积分学方法来解题

积分学方法主要有定积分和重积分两种。当证明与自然数n相关的不等式时，多采用定积分方法来求证。例如：当存在某一正常数A＜1时，对于任意的n＞0，都有不等式成立。在求证中，我们利用定积分方法，可以得出A=，从而得出不等式成立。

在利用定积分求证不等式过程中，还可以利用定积分中值定理来消去不等式的积分号，从其他项的大小比较中来求证。例如：当函数 f（x）是连续且单调递减时，求证当 0＜λ＜1时，存在首先对不等式进行移项，转变为

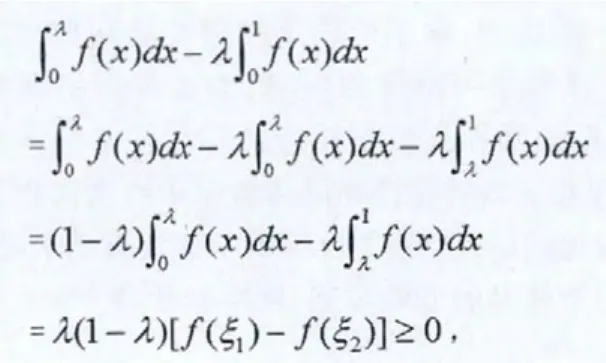
当不等式包含两个定积分之积时，可以利用重积分来进行证明。例如：证明不等式在证明过程中，可以利用则假设 D1：0≤即可以得出成立。

3 利用其他方法来解题

对于不等式的求证方法，比较常见的还有泰勒公式法，此方法适用于有函数的一阶、二阶及二阶以上的导数且最高阶导数的大小或上、下界可知的命题。例如且满足 f″（x）≥0，试求证f（x）≥x。对于该题在求证时，从已知中可以得出，则有 f（x）=f（0）+f′（0）x+代入得到其中 ξ∈（0，x）。由题设 f″（x）≥0，可知，f（x）≥x。

另外，在不等式的证明过程中，还可以利用概率论方法来求解。如当取值范围在0和1之间时，可以将不等式转化为若干独立的事件概率，以便于求证。例如：当 0＜a＜1，0＜b＜1 时，试求证0≤a+b-ab≤1。对于题设中的a，b来说，可以看作是两个独立的事件，当 P（A）=a，P（B）=b 时，很容易得出 0≤a+b-ab≤1。