具有随机利率的分数型复合期权定价模型
2014-10-16杨淑彩王晓东
杨淑彩,薛 红,王晓东
(西安工程大学 理学院,西安710048)
复合期权是以标准的期权作为标的资产的期权,有四种基本形式:看涨期权的看涨期权、看跌期权的看涨期权、看涨期权的看跌期权、看跌期权的看跌期权.毕学慧[1]在利率确定情形下用保险精算方法给出了股票价格服从几何布朗运动的复合期权定价公式,赵建国[2]用鞅方法给出了风险中性条件下跳-扩散模型下的复合期权定价公式.
在上述模型中,利率都是常数或者为时间的非随机函数,但是在现实市场中,利率会呈现一定的随机性.当然这种变化并不是漫无边际的,大量事实表明,利率存在均值回复行为.文献[3]建立了随机利率下可转换债券定价数学模型并得到可转换债券的定价公式,文献[4]讨论了基于随机利率下跳-扩散过程的复合期权的定价.
近年来,大量的事实表明,股票价格具有“尖峰、厚尾”的特点,同时具有长期相关和自相似性等特征,这是布朗运动所不能体现出的,而分数布朗运动正好具备这种特征,且当H=时,分数布朗运动即为布朗运动.文献[5]在分数布朗运动环境下利用偏微分方程方法得到了欧式期权定价公式,文献[6]用偏微分方程方法得到分数布朗运动下随机利率情形的欧式看涨期权的定价公式.
本文考虑利率服从Vasicek随机利率模型,资产价格服从分数布朗运动驱动的随机微分方程,用随机分析理论推出复合期权的定价公式,推广了复合期权定价模型,使之更加贴近实际的金融市场.
1 预备知识
定义 1[7]设 H∈(0,1)为一常数,具有 Hurst参数为H,概率空间(Ω,F,P)上的分数布朗运动是一个高斯过程{WHt,t≥0},且满足

如果 H=0.5,则 WHi为标准布朗运动,用Wt表示.
引理 1[8]若(X,Y)~N(μ,Σ ),其中

其中:N(·)是标准正态分布的分布函数.

其中:φ(Y)是随机变量为Y的函数,N(·)是标准正态分布的分布函数.
证明 E[eXN(φ(Y))I{Y≥b}]=
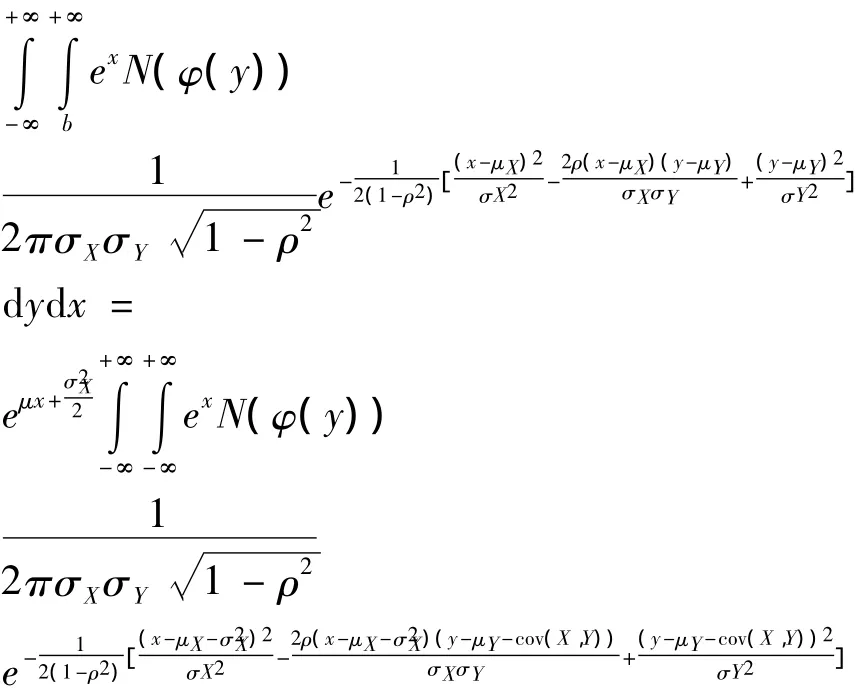

等式(2)同理可证,证毕.
2 市场模型
假定(Ω,F,P)为风险中性概率测度空间,且利率和股票价格分别满足下面的随机微分方程

其中:σ >0,a,b,c为常数;{WH(t),t≥0}和{BH(t),t≥0)为(Ω,F,P)上的分数布朗运动,且相互独立;{Fi=σ(0≤s≤t),t≥0)}为信息流.
定理1 随机微分方程(2)的解为.
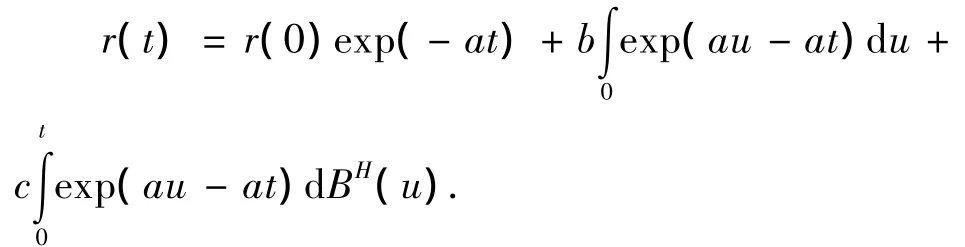
证明 由分数型Ito公式
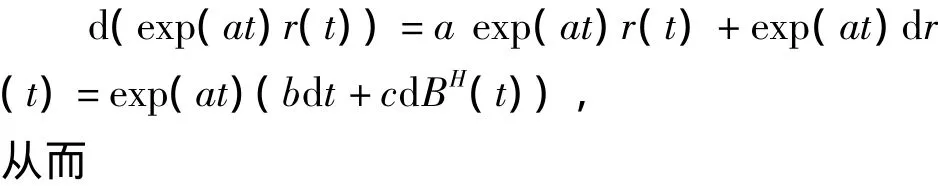

由此可得结果.
定理2[9]随机微分方程(1)的解为

3 随机利率下欧式期权的定价
由风险中性定价理论知,到期日为T,执行价格为K的欧式看涨期权在t(0≤t≤T)的价值为

则C1为常数,且
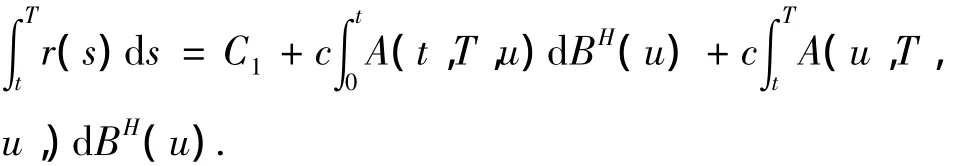
定理3 到期日为T,执行价格为K的欧式看涨期权在时刻T0(0≤T1≤T)的价值为

其中

证明 欧式看涨期权在时刻t(0≤t≤T)的价值为

下面我们先计算II:

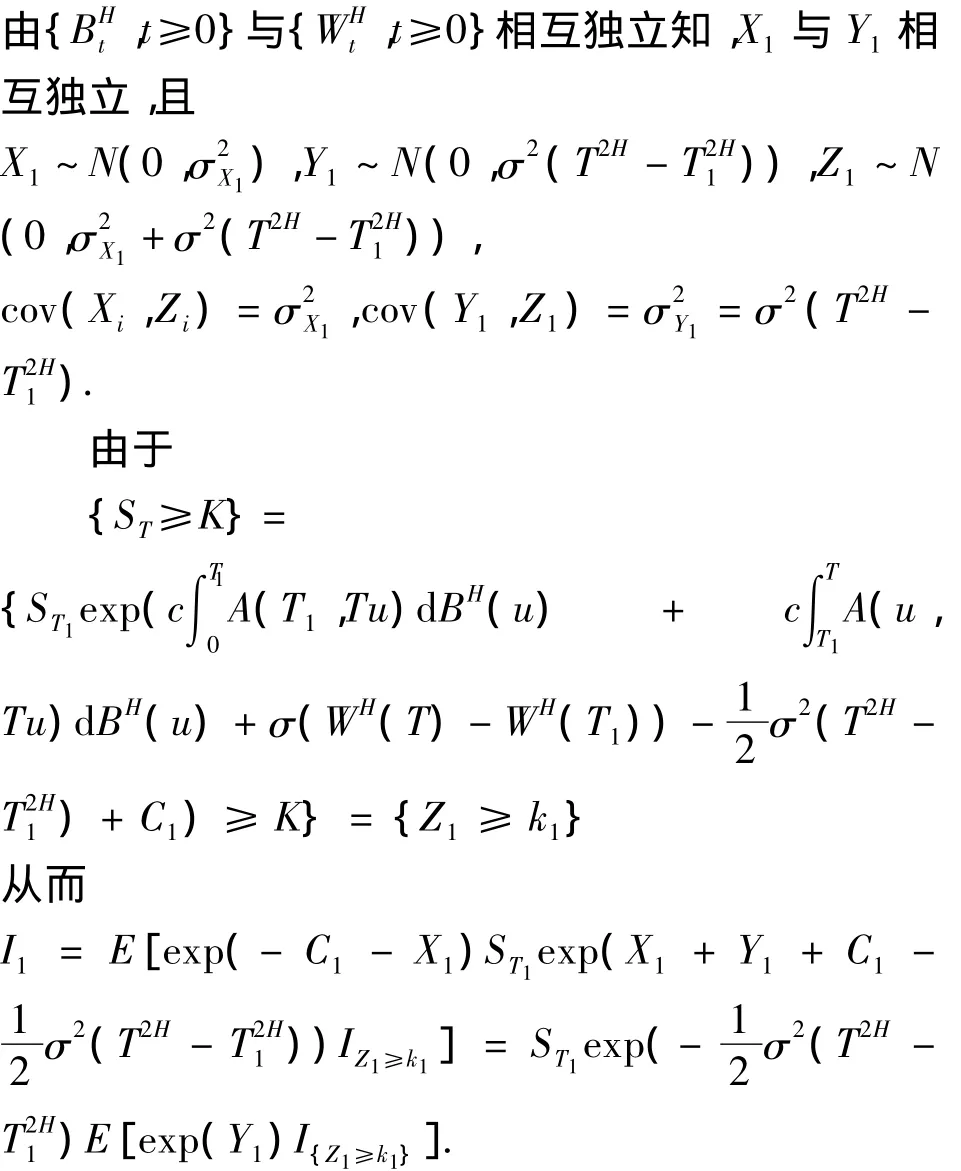
由引理1有
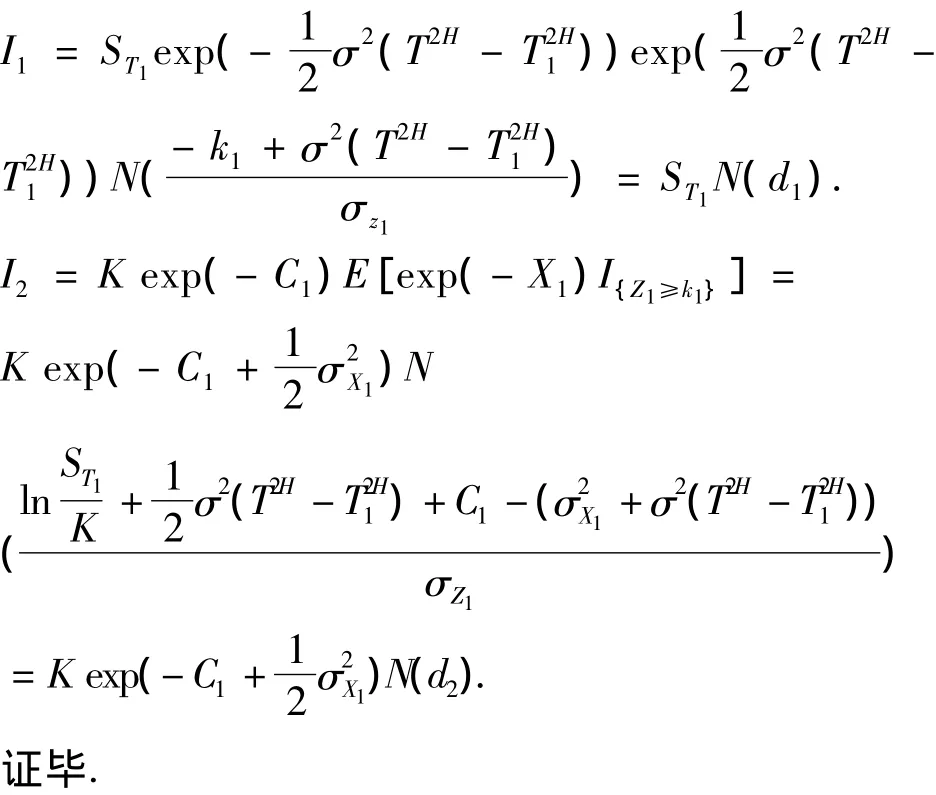
定理4 欧式看涨期权的价格函数CE(x,K,T1,T)关于x是严格单调递增的.

定理得证.
4 随机利率下复合期权的定价
定理5看涨期权的到期日为T,执行价格为K,看涨期权的看涨期权到期日为T0,执行价格为K1的复合期权在时刻T0(0≤T0≤T1)的价格为

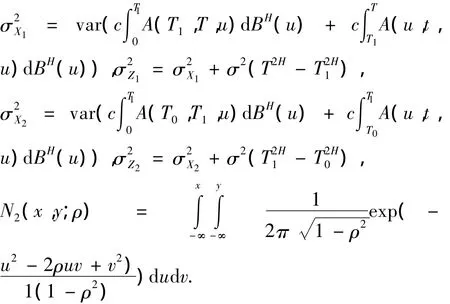
N(·)是一维标准正态分布的分布函数;N2(·)是二维正态分布的分布函数,其相关系数为ρ.

从而看涨期权的看涨期权在时刻T0(0≤T0≤T1)的价格为



同理由引理2可计算(b),即
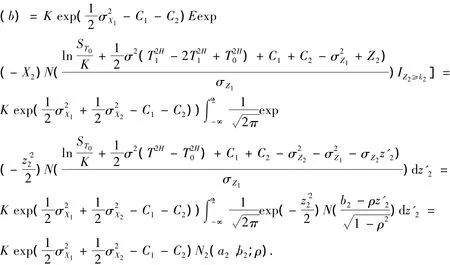
由引理1可得
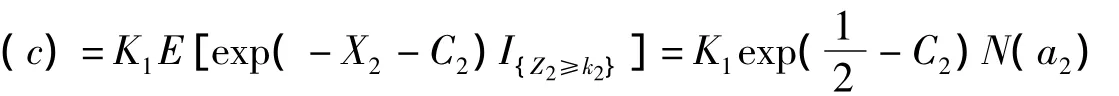
综上所得,结论得证.
推论1 当a→0,b→c,c→0时,可得常利率下复合期权定价公式为
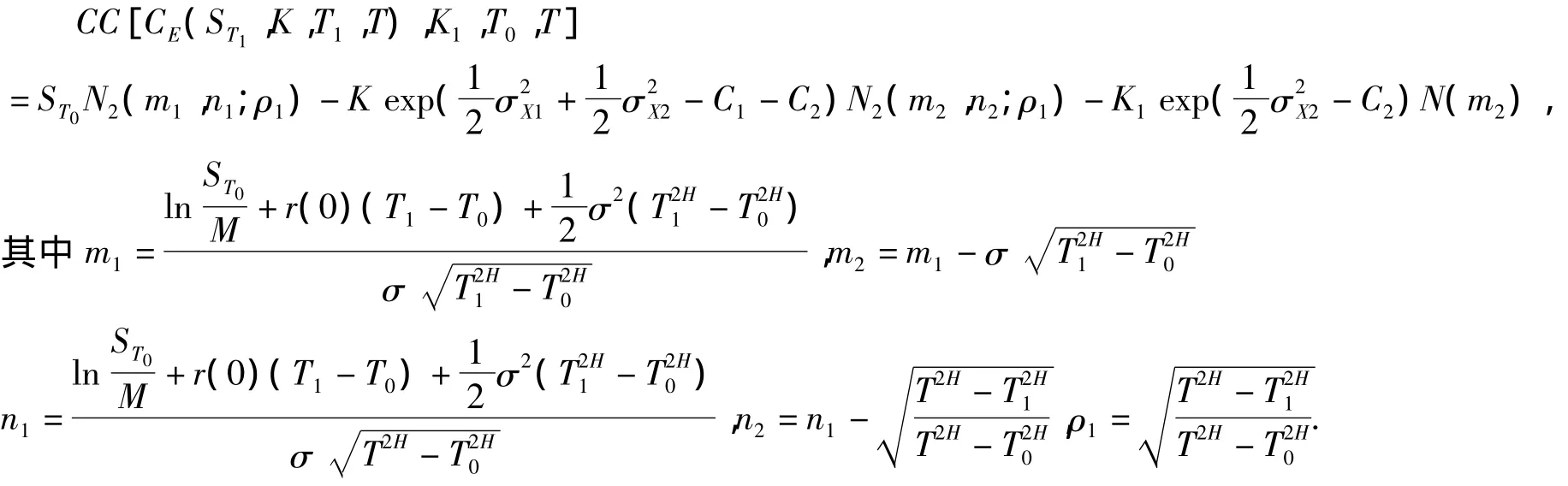
这与文献[10]不含跳的结果是一致的.

其中
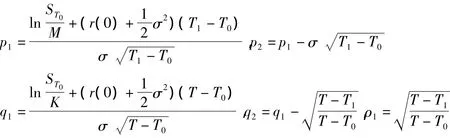
也就是文献[11-13]的结果.
5 结语
本文首先假定利率是随机的,服从Vasicek随机利率模型,资产价格服从由分数布朗运动驱动的随机过程.其次用风险中性方法,给出了此模型下欧式复合期权的定价公式.本文同时考虑利率是随机的和资产价格是由分数布朗运动驱动的随机微分方程这两种情况,推广了有关复合期权的文献的结果.
[1]毕学慧,杜雪樵.复合期权的保险精算定价[J〛.合肥工业大学学报,2008,31(8):1343-1346.
[2]赵建国,师 恪.跳-扩散模型下的复合期权定价公式[J].新疆大学学报,2006,23(3):257-264.
[3]薛 红,李 军,吴晓蕊.随机利率下可转换债券定价[J].西安工程大学学报,2011,5(1):119-121.
[4]李翠香,石 凌.基于随机利率下跳-扩散过程的复合期权的定价[J].黑龙江大学自然科学学报,2012,29(4):431-436.
[5]孙玉东,薛 红.分数型欧式期权定价模型[J].纺织高校基础科学学报,2009,22(2):204-206.
[6]张 超,张寄洲.分数布朗运动下随机利率情形的欧式期权定价公式[J].上海师范大学学报,2010,39(6):558-562.
[7]GUASONI P.No arbitrage under transaction costs with fractional Brownian motion and beyond[J].Mathematical Finance,2006,16(3):569-582.
[8]ZHANG S,YUAN S,WANG L.Prices of Asian options under stochastic rates[J].Applied Mathematics-A Journal of Chinese Universities,2006,21(2):135-142.
[9]张学莲,薛 红.分数布朗运动环境下重置期权定价模型[J].西安工程大学学报,2009,23(4):141-145.
[10]方 知,何传江,王 艳.服从分数跳-扩散过程的复合期权定价[J].数学的实践与认识,2011,41(12):6-14.
[11]张鸿雁,李 滚.欧式复合期权的定价公式[J].经济数学,2005,22(4):384-388.
[12]党柳梦,薛 红,卢俊香.分数布朗运动环境下欧式篮子期权定价[J].哈尔滨商业大学学报:自然科学版,2013,29(5):598-599,613.
[13]李琛炜,薛 红.分数布朗运动环境下可转换债券定价模型[J].哈尔滨商业大学学报:自然科学版,2013,29(2):254-256.
