短行程高加速运动平台模型辨识研究
2014-10-16刘武龙刘扭扭刘延杰
刘武龙,刘扭扭,刘延杰
(哈尔滨工业大学机器人技术与系统国家重点实验室,哈尔滨150001)
系统模型辨识就是在输入和输出数据的基础上由规定的一类系统模型中确定一个系统模型,使之与被测系统等价[1-2].系统模型辨识方法有很多,如脉冲响应法、M伪随机序列法、最小二乘法以及频率响应测试法[3-6],脉冲响应法易受驱动器零漂等影响,激励不足;M伪随机序列法辨识精度不够.本文采用扫频实验的方法,但由于平台行程较短(毫米级)、加速度较高(大于50 m/s2),低频激励时易超出行程,故采用组合正弦波作为输入信号,选取合适的幅值和频率,测量系统响应,然后利用Matlab对输入输出信号进行频谱分析,再对频率响应进行拟合,计算系统模型辨识.
实验系统硬件平台,包括自行研制高加速精密运动平台、dSPACE实时仿真系统、精密光栅尺.软件平台,包括dSPACE计算机控制系统设计工具包、Matlab/Simulink软件、dSPACE公司 Con-trolDesk软件.dSPACE实时系统主要由三部分组成,如图1所示.

图1 dSPACE实时系统构成
1 实验原理与设计
频率响应测取,使对象的输入量为x(t)=B1sin(ω1t),待对象输出量y(t)呈现出稳定的正弦波变化后,可得y(t)=A1sin(ω1t+φ).计算机采集到数据后可形成文件,并画出曲线,如图2所示,其幅值比 A(ω1)=A1/B1,其相位差 φ(ω1)= - Δt×2π/T1,这就是频率特性曲线中的一个点.根据对象的性质,选择15~40个不同的角频率ω,为在对数曲线均匀取值,得到频率响应曲线的必需点.因为 lgω =lg2πf=lg2π +lg f,按 f=10x,取 x 值,均匀地取从所关心的2 Hz~1 kHz间取40个数,对f进行四舍五入取整处理,再换算成角频率ω=2πf,输入系统中,系统频率响应与对应频率如表1所示.为缩短实验时间,采取多个正弦信号组合的方式,如 x(t)= ∑Nk=1aksin(ωkt+φk),再采用谐波分析方法从总的输出波形中获得各个频率的输出波形,进而同时获得多个频率下的频率特性,模型辨识框图如图3.

表1 系统频率响应与对应频率表

图2 正弦波测试曲线

图3 伺服系统模型辨识实验设计框图
2 实验数据与处理
按照以上实验设计开始实验,启动计算机与dSPACE系统,运行程序,待平台运动稳定后,保存输入电流信号、输出速度信号,利用Matlab编写M文件,对所获得数据进行fft变换,如图4所示.

图4 系统输入输出fft信号(100~270 Hz)
对系统输入、输出信号进行频谱分析,可得每个频率信号下的输入、输出信号幅值比,与相位差.以输入输出信号幅值比作为系统幅值,输入输出信号相位差作为系统相位,即

由此,可得系统的频率特性,H(jω)=A cos(ωt+ φ)+jA sin(ωt+φ).
由频响求取传递函数,利用Matlab中由频率响应求取传递函数的功能函数invfreqs,[b,a]=invfreqs(H,ω,n,m)为其调用格式,其中:n 为传递函数分子阶数;m为传递函数分母阶数;H为系统频率响应;ω为频率响应对应角频率;返回量b,a分别为所要求取传递函数分子、分母系数.
由以上条件,求得系统辨识速度-电流模型为

3 模型验证
为了验证模型的准确性,在离线仿真条件下对所辨识的模型进行PID位置闭环控制系统设计,再把该PID控制器带入dSPACE实时控制系统.比较同一PID控制器下离线、在线的系统位置响应曲线,验证辨识模型的准确性.图5为离线PID控制仿真程序,位置参考输入采用S型速度曲线规划,以70 m/s2的加速度加速到0.42 m/s,再以 -70 m/s2加速度减速到0,对速度曲线进行积分运算,得到位置参考输入,整个过程平台运动2.54 mm,运行时间12 ms,调节PID参数为
P=32,I=0.5,D=0.5
此时离线仿真位置闭环阶跃响应如图7虚线,再将PID控制带入dSPACE半物理仿真环境中,如图6为dSPACE实时系统控制框图.给定同样信号,系统响应曲线如图7实线,可以看出,二者响应曲线有较好重合度,最大偏差5%,实验表明:模型辨识是正确的,本辨识方法是可行的,可以参照此系统模型进行控制算法设计及分析.
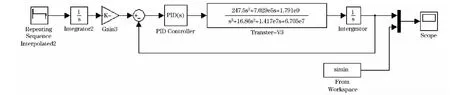
图5 离线仿真控制框图
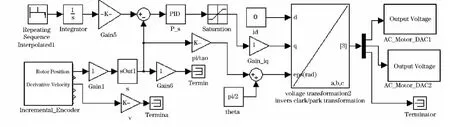
图6 d SPACE实时系统控制框图

图7 辨识模型准确度验证
4 结语
利用dSPACE半物理仿真环境,对高加速运动平台进行系统模型辨识研究,通过对比离线仿真与半物理仿真阶跃响应结果,证明了辨识结果是可信的.本文使用的通过测取系统在不同频率信号下的频率响应,获取系统模型的方法安全、可靠、易实现,且较为准确地获得系统的频率特性.
[1]潘立登,潘仰东.系统辨识与建模[M].北京:化学工业出版社,2004.
[2]刘党辉,蔡远文,等.系统辨识方法及应用[M].北京:国防工业出版社,2010.
[3]侯媛彬,汪 梅,等.系统辨识及其MATLAB仿真[M].北京:科学出版社,2004.
[4]郭立辉,朱励洪,高 巍.基于MATLAB的最小二乘法系统辨识与仿真[J].许昌学院学报,2010,29(2):24 -27.
[5]邓春龙,许伟明,张 昕.相关函数脉冲响应法系统实时辨识[J].测控自动化,2012,28(3):29 -31.
[6]张立勋,董玉红,王怀军.基于半物理仿真技术的机电伺服系统模型辨识研究[J].机电一体化,2006(2):30-32.
