基于误差模型的混合分类算法

丛雪燕

(抚顺职业技术学院信息工程系，辽宁 抚顺 113122)

0 引言

数据挖掘方法可以分为监督学习和非监督学习2种方法。监督学习方法是一种预先指定目标变量的方法，它需要一组训练的数据集，这组数据集是历史数据所提供的有效目标变量。分类是一种很普遍的数据挖掘方法，在分类过程中，需要验证新产生数据的特征并将它划分到一个预先确定的集合中。在分类过程中，经常遇到的一个重要问题是对于一个特殊的问题如何选择最适合的方法。许多学者试图找到最好的算法和输入/输出数据变量类型之间的联系，研究得出的结论是:对于数据挖掘不存在一个普遍的最好的执行方法，即不同的方法有它们自己的优点和不足。所以，一个方法对一个特殊的问题可能是最佳的，但是对于另外一个问题，其他的方法可能更好，这种情况称为选择性优势。同样，这种情况也说明，所有的监督学习方法在提高分类精度上有它们固有的局限性。本文针对目标变量是二进制的数据集合，提出一种新的混合分类方法来提高分类的精度，该方法克服了采用单一监督学习方法的缺点，通过结合不同方法的相似概念影响的联合作用，对已经划分的有效训练数据集合反复地应用相同的算法，改进分类性能，提高分类精度，减少由于经验和不一致产生的误差。

1 误差模型的混合分类算法

1.1 定义和符号

在提出基于误差模型的混合分类算法之前，先描述一下本文用到的符号和相关的概念。预报器是通过监督学习方法而产生的预报逻辑，用神经网络或决策树归纳技术对一组训练的数据集进行监督学习来产生一个预报逻辑。例如，一个通过决策树归纳技术产生的预报器是一组多重的决策规则的集合;一个通过神经网络产生的预报器分别由相应的输入向量和目标向量所构成的输入和输出结点所组成。

本文中，笔者考虑的预报器是二进制目标值。如果一个预报器ψ由数据挖掘方法A和训练的数据集L所产生，那么预报器ψ是一个定义在输入向量和目标向量集合上的一个函数，它表示为ψA(·|A)。一个输入变量第i种情况的向量的预测值定义为ψA(xi|A)，它由(pi，Pr ob(pi))组成，其中 pi是二进制的预测值，Pr ob(pi)是pi的概率。

1.2 基本思路

假设采用监督学习方法预测10组实际值的目标变量，预测时运用2种算法:算法A(如决策树归纳技术)和算法B(如人工神经网络)。实际值、算法A和算法B的预测值如表1所示。在本例中，算法A和算法B的预测精度都是70%(7组)。从2种算法的全部误差率来看，它们具有相同的性能。然而，如果对表1中的预测结果进行更加细致的观察，就会发现有2组记录(第8组和第10组)显示2种算法都得出了错误的结论，而另2组记录(第3组和第9组)显示2种算法得出了不同的结论。也就是说，这2种算法的预测结果必然符合以下3种情况的一种:都是正确的、都是错误的、只有一种是正确的。这时如果有一种混合算法能够在A、B这2种算法预测的结果不一致时，知道哪种算法工作得比较好，那么预测的精度将能提高到80%，如表1中的最后一列所显示的。当然，完全知道哪一种算法工作得较好是不可能的，然而用监督学习方法，笔者可以确认输入向量和决定较好方法的模式。

表1 监督学习方法预测举例

1.3 基于误差模型的混合分类算法

首先，将训练数据集分解成2个子集，利用一个数据子集，应用2种或多种不同的监督学习方法获得预报器。产生的预报器被应用到另一个数据子集中，将2种或多种不同的监督学习方法得到的不同预测结果从数据集中抽取出来;用抽取出来的数据集，训练对一个特殊的输入向量有正确输出的方法，即产生了新的预报器。新的预报器能够确定对于给定的输入向量和哪种方法能够预测出更精确的结果。新产生的预报器可称为误差模型。误差模型将2个先前应用监督学习方法的预测结果合并，提高预测不一致情况时的预测精度。

基于误差模型的混合分类算法的详细描述如下:

(1)设 L={(xn，yn)|n=1，2，3，…，N}为训练数据集，yn是目标向量，xn是输入向量，N是数据集的数量。在数据集中，TL是数据集L的目标向量的列。从训练数据集验证预测逻辑的测试数据集为Lt={(xt，yt)|t=1，2，3，…，T}。

(2)训练数据集通过随机采样被分为2个数据集。2个数据集表示如下:

其中M+P=N。

(3)用方法A和数据集L1进行学习，产生预报器ψA(·|L1)。同样，用方法B和数据集L1进行学习，产生预报器ψB(·|L1)。

(4)把用数据集L1和A、B两种方法产生的预测逻辑的预报器ψA(·|L1)和预报器ψB(·|L1)，应用于另外一个训练的数据集 L2，使 T(A，L2)和 T(B，L2)各自成为预测结果ψA(·|L1)和ψB(·|L1)的列。算法描述如图1所示。

图1 应用2个监督学习方法对训练数据集进行划分

(5)把在数据集L2上产生的预测结果ψA(·|L1)和ψB(·|L1)进行比较，并抽取不同的预测结果记录。与在表1中抽取记录3和记录9的过程是相似的。将抽取的数据集作为 L(2，e)，即 L(2，e)={(xi，yi)|L2and ψA(xi|L2)≠ψB(xi|L2)}。被抽取的数据集作为训练数据集用来产生误差模型，然后从抽取的数据集L(2，e)产生新的目标向量。

(6)产生的新的目标向量将表明方法A的预测结果是否正确。即，如果(xi，yi)∈L(2，e)中的 yi等于ψA(xi|L1)，那么新的目标向量被赋予T(真)，否则被赋予F(假)。从目标向量得出的新增加的列表明了T(A，L(2，e))。同样的，一个新的目标向量 T(B，L(2，e))也产生了，即，如果(xi，yi)∈L(2，e)中的 yi等于 ψB(xi|L1)，那么 T(B，L(2，e))被赋予 T(真)，否则被赋予 F(假)。

(7)从数据集 L(2，e)中抽取的目标向量 T(A，L2)被新的目标向量 T(A，L(2，e))取代，结果数据集用 L'(2，e)表示，并用方法A和L'(2，e)进行学习。同样的，原始的目标向量被 T(B，L(2，e))取代，结果数据集用 L″(2，e)表示，并用方法B和L″(2，e)进行学习。用方法A和目标向量产生预报器ψA(·|L'(2，e))，用方法B和目标向量产生预报器 ψB(·|L″(2，e))，这个过程如图2 所示。

图2 产生误差模型和新目标向量的过程

(8)预报器 ψA(· |L'(2，e))和预报器 ψB(· |L″(2，e))的含义是当方法A和方法B产生不同的预测结果时，通过新的目标向量来确定哪种方法能产生更有效的预测逻辑，则预报器 ψA(·|L'(2，e))和预报器ψB(·|L″(2，e))称为误差模型。

(9)当获得误差模型后，将选出最终的预报器模型。例如，对于测试数据集 Lt={(xt，yt)|t=1，2，3，…，T}中每一个 xt作用于预报器 ψA(·|L'(2，e))，如果预测的结果是 T，将预报器ψA(·|L1)应用到xt，否则将预报器ψB(·|L1)应用到xt，这种方式产生的预报器模型表示为 ψ(A，B)(·|L)，如图3所示。然后，将相同的 xt作用于预报器 ψB(·|L″(2，e))，如果预测的结果是T，将预报器ψB(·|L1)应用到xt，否则将预报器ψA(·|L1)应用到xt，这种方式产生的预报器模型表示为ψ(A，B)(·|L)，如图3所示。合并2种预测结果，当与ψ(B，A)(·|L)预测结果不同时，较高的预测概率的值作为最终的预测值。最终的预报器模型表示为ψ(A，B)(·|L)，见表2和表3，即表2中有4个预测值的记录 ψA(·|L'(2，e))、ψB(·|L″(2，e))、ψA(·|L1)和ψB(·|L1)，表3 中确定了 ψ(A，B)(·|L)，ψ(B，A)(·|L)和 ψ〈A，B〉(·|L)的值，则 ψ〈A，B〉(·|L)是提出的基于误差模型的混合分类算法的最终预测值。

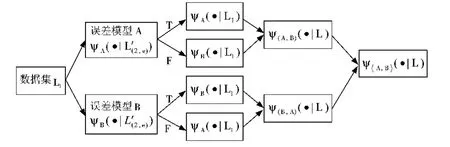
图3 最终预报模型产生示意图

表2 2种算法的识别结果

表3 2种算法的选择结果

该算法主要是通过不同方法和数据的应用提高预测精度。运用误差模型，能得到比单一监督学习算法更好的性能。提出的混合分类算法需要更多的计算时间;在分割训练数据集后对于每一次的学习过程都减少了训练数据集的规模，这样会使产生的预报器不稳定，尤其当训练数据集的总数较少的时候。

2 实验结果与分析

2.1 实验中的假设

为了验证提出的混合算法，笔者用实测的数据集合进行实验。①首先进行实验数据集的采集，并把采集的数据转化为二进制数据类型;②实验使用SPSS公司的Clementine 8.1数据挖掘软件，但提供的各种选项不能修改;③多层神经网络和决策树归纳算法与混合算法进行比较。因为它们是典型的分类方法，在分类方法上都有各自的优点，例如神经网络是一种黑盒逼近，而决策树方法对分类结果进行解释。

2.2 实验数据集的描述

在实验中，笔者采用问卷调查和网上调查的方式进行数据集的采集，共采集了6组数据集，并将采集的数据集转化为二进制，实测数据见表4。

表4 实测数据

2.3 实验结果

对于实测的数据集合，表5给出了简要的实验结果。表5中包括了数据集记录的总数、测试数据集的数量、神经网络准确度、决策树算法的准确度、神经网络和决策树算法选择的准确度和提出的基于误差模型的混合算法的准确度。在表5的第4列，是神经网络和决策树算法预测不一致的数量和比率。在6组数据集中，对提出的基于误差模型的混合算法都可得到最好的性能，表5中的结果显示用误差模式模型的混合方法的精度等于或高于神经网络、决策树算法等单一的监督学习方法。

从表5中能够发现，基于误差模型的混合算法准确度的提高并不是相同的。例如，对于1号和4号数据集，准确度比传统的神经网络和决策树算法提高了10% ～20%以上，然而，对于3号和5号数据集，准确度仅仅提高了0～0.3%。这种不同的原因在于，2种监督学习算法的预测不一致的比率，1号和4号数据集的预测准确度比其他的数据集有很大的提高，而2种监督学习算法的预测不一致的比率高达31.29% ～48.53%。相比之下，3号和5号数据集的预测不一致的比率较低，它们的预测准确度的提高是轻微的。

基于误差模型的混合算法性能的提高与2种监督学习算法预测的不一致率有较高的相关性。因此本算法适合于当2种或2种以上监督学习算法分类不一致率较高的情况。从表5中也能发现，数据集的数量与本算法的改进没有很重要的联系。

表5 实验结果

3 结束语

本研究提出了一种基于误差模型的混合分类算法。在该算法中，一个训练数据集首先被分割成2个数据子集。用一个训练数据子集和2个不同的监督学习方法产生2个预报器。2个预报器应用到另外一个训练数据集中，抽取出2个预报器产生的不同预报的情况。用抽取的数据情况，2个不同的学习方法再一次被应用，用来获得预测逻辑的误差模型，该预测逻辑决定当2个预报器产生不一致的预测结果时，哪一个预报器运行得好。应用误差模型和选择技术，从2个预报器中确定最终的分类结果。通过6组实际数据集，验证了本研究提出的方法的预测性能，并与传统的单一学习算法进行了比较。实验结果表明，该算法预测精度优于单一学习算法，特别是，当2种不同的监督学习算法的预测不一致率很高时，该算法的性能有很大的提高。该算法在对预测精度很重要时很有效，例如，在信用卡或医疗欺诈的情况下，一个信号会引起一系列的危害。然而，当2种不同的方法预测不一致比率非常低，或者一种方法的性能绝对优于另一种方法时，则该方法的有效性是无关紧要的。该方法与采用单一方法相比需要多次的计算则是它的缺点。然而，由于提高了计算速度，该局限性并不是十分重要。

［1］Webb G I，Zheng Z.Multistrategy ensemble learning:Reducing error by combining ensemble learning techniques［J］.IEEE Transactions on Knowledge and Data Engineering，2004，16(8):980-991.

［2］Wong M L，Lee S Y，Leung K S.Data mining of Bayesian networks using cooperative coevolution［J］.Decision Support Systems，2004，38(3):451-472.

［3］Zhang Z，Zhang C.Agent-based Hybrid Intelligent Systems:An Agent-based Framework for Complex Problem Solving ［M］. Berlin， Heidelberg:Springer-Verlag，2004:127-142.

［4］Versace M，Bhatt R，Hinds O，et al.Predicting the exchange traded fund DIA with a combination of genetic algorithm and neura1 networks［J］.Expert Systems with Application，2004，27(3):417-425.

［5］Hsu P L，Lai R，Chui C C，et al.The hybrid of association rule a1gorithms and genetic algorithm for tree induction:An example of predicting the student course performance［J］.Expert Systems with Application，2003，25(1):51-62.

［6］Taylor D E，Turner J S.ClassBench:A packet classification benchmark［J］.IEEE/ACM Transactions on Networking，2007，15(3):499-511.

［7］李玲俐.数据挖掘中分类算法综述［J］.重庆师范大学学报:自然科学版，2011，28(4):44-47.

［8］谷琼，袁磊，宁彬，等.一种基于混合重取样策略的非均衡数据集分类算法［J］.计算机工程与科学，2012，34(10):128-134.

［9］蔡巍，王永成，李伟，等.An experimental comparative study on three classification algorithms［J］.Journal of Shanghai Jiaotong University(Science)，2003，8(2):133-136.

［10］Qu Huaqiao，Zhang Shichao，Liu Huawen，et al.A multilabel classification algorithm based on label-specific features［J］.Wuhan University Journal of Natural Sciences，2011，16(6):520-524.

［11］Charu C Aggarwal，陈辰，韩家炜.The inverse classification problem［J］.Journal of Computer Science＆ Technology，2010(3):458-468.

［12］梁燕，徐向阳，吴晓峰.基于半监督的联合分类方法［J］.计算机工程与设计，2013，29(9):2328-2329，2332.

［13］王秀美，高新波，李洁.一种基于高斯隐变量模型的分类算法［J］.计算机学报，2012，35(12):2661-2667.

［14］于重重，商利利，谭励，等.半监督学习在不平衡样本集分类中的应用研究［J］.计算机应用研究，2013，30(4):1085-1089.