基于GoogleEarth的飞行等待程序三维模拟实现

2014-10-15潘卫军

计算机与现代化 2014年1期

潘卫军，李丘

(中国民航飞行学院空中交通管理学院，四川广汉 618307)

0 引言

仿真技术对于模拟和呈现现实世界中客观事物的发展、变化和运行规律起着重要作用，利用飞行仿真器在地面训练飞行员，可以节省大量燃料和经费而且不受气象条件和场地的限制。此外，利用飞行仿真器还能模拟空中运行中可能遭遇的特殊情况，培养飞行员和管制员应对特殊情况的能力，具有较高的安全性。通常民航飞行和航空运行保障人员需要及时掌握飞行动态，都希望能有一种直观方便的三维仿真方法来模拟航空器飞行动态，以帮助他们解决实际工作中遇到的问题。本研究以GoogleEarth(GE)软件为平台，结合软件编程实现飞行等待程序三维飞行模拟仿真。

1 飞行等待程序中航迹点经纬度计算方法

1.1 飞行等待程序

飞行等待程序由定位点、出航转弯、出航边、入航转弯、入航边组成，等待定位点通常以 NDB/VOR、VOR/VOR、VOR/DME作为定位点。其中NDB为无指向性无线电信标(Non-Directional Beacon)，VOR为甚高频全向信标(Very High Frequency Omnidirectional Radio Range)，DME为测距仪(Distance Measure E-quipment)，可分为出航转弯向右的右等待航线以及出航转弯向左的左等待航线，其中右等待航线为标准等待航线。如图1所示。

图1 标准等待程序示意图

等待航线飞行要求满足相关规定:(1)进入等待程序和在等待程序上飞行时飞机的指示空速应等于或小于给定的速度;(2)转弯坡度为25°或标准转弯率3°/s对应的坡度，以所需坡度小者为准;(3)飞机出航航段的静风飞行时间，在飞行高度4250m(14000ft)或以下1分钟，在4250m(14000ft)以上为1.5分钟，如果DME可用，则出航航线的长度可用DME距离代替时间;(4)出航计时是从正切等待点时开始，如不能确定正切位置，则在完成转弯至出航航向即开始计时。

1.2 直线运动轨迹经纬度点的计算

定义:等待程序等待定位点H(eH，nH)，eH为等待定位点经度，nH为等待定位点纬度;航空器飞行轨迹上任意一点P(ei，ni)，ei为第i点经度，ni为第i点纬度;入航真航线角Tc;航空器真空速TAS，单位为千米每小时(km/h);等待航线高度Alt，单位为米(m);出(入)航时间t，单位为秒(s);航空器转弯率W，单位为度每秒(°/s)，等待程序飞行中航空器的主要飞行状态为直线飞行和转弯飞行2种状态。

根据贝塞尔大地主题正解算法进行推算。贝塞尔大地主题正解算法为:在球面上两点，已知第一点的经纬度坐标，第一点至下一点的大地方位角以及大地线长度对下一点经纬度坐标进行求解的过程，推算结果如下:

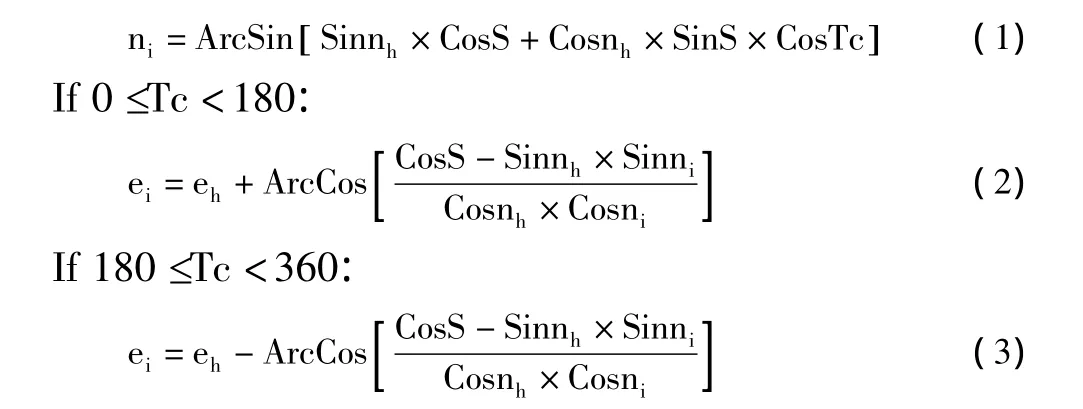
根据上面的模型对i进行循环，求解公式便可以得到航空器直线运动的任意点的经纬度坐标。

1.3 转弯运动轨迹经纬度点的计算

然后计算P点经纬度，模型如下:

根据上面的公式对i进行循环求解模型，便可以得到航空器转弯运动的每一点经纬度坐标。对于左转弯的计算模型，只要将右转弯模型做个镜像就可以得到。

2 基于GE的三维仿真技术

GE软件是一款便捷的GIS(地理信息系统)软件，能够为用户提供完全免费的全球卫星遥感影像数据，并且可以使用基于XML语言格式的KML文件来表达三维空间，实现一些特殊自定义的功能。KML文件全称为Keyhole标记语言(Keyhole Markup Language)是GE中表达三维空间以及单位的重要工具文件，是一种基于XML语法与格式语言的文件，可以用来描述和保存用户所需要的地理信息(如点、线、图像、多边形和3D模型等)，并且被GE识别并显示。

KML文件中表达的基本类型有地标点类、路径类、多边形类、模型类以及地面叠加层类5种，关键标签依次为:＜Point＞、＜LineString＞、＜Polygon＞、＜Model id=""＞、＜GroundOverlay＞，地标点类就是一个点元素，在KML文件中可以定义出这个点元素的各项属性，如样式、颜色等，并且在＜Point＞标签中定义出它的经纬度位置，如＜coordinates＞102，14＜/coordinates＞在飞行等待程序仿真中需要实现飞机模型在GE中沿飞行航线进行飞行的效果，所以路径类、模型类是需要应用的主要元素类型。

GE是一个开放的三维平台，对于三维模型的导入是不可缺少的功能，常见的三维制图软件模型都可以直接导入GE系统。如3D-Max、SkechUp等，下面是一段导入三维模型的KML代码:

这段KML代码是一段标准的定义模型类元素的代码，其中的＜name＞标签定义模型的ID，＜altitudeMode＞标签定义模型高程形式，absolute表示绝对高度，即以标准海平面为基准零平面的高度，在对航空器飞行行为模拟中的＜Location＞与＜Orientation＞2个标签定义的属性分别是航空器的三维大地空间坐标以及航空器的航行姿态，＜Orientation＞主要是对航空器的空间六自由度进行控制，即分别为偏航、俯仰与滚转，＜Scale＞标签定义模型分别在XYZ三个方向上大小，＜Link＞标签定义所插入模型的引用位置。

通过上述方法可以在GE中引入航空器模型，此外让航空器模型在GE空间中运动是实现飞行模拟的重要步骤。要让航空器在GE中运动实际上是实现模型类元素在GE中的动态显示，GE软件实际上是一款包含时间轴的四维平台，要实现模型元素的动态显示只要合理地利用时间轴便可以实现。用到的关键标签是＜TimeStamp＞如＜TimeStamp＞＜when＞日期时间＜/when＞＜/TimeStamp＞这段代码定义了一个日期时间点，它可以定义模型的产生时间，这样在KML文件中对各个时间点上模型的各项状态以及空间位置信息进行定义，再以一个适当的仿真速进行运行，结合控制GE中的时间轴工具，便可以实现模型随时间流逝的动态显示，每一时间点间的间隔相当于动态影像的1帧。如果间隔的跨度定义得越小，帧与帧之间的过渡就越平滑。理论上当帧速达到24帧/秒时，飞机模型的动态显示在视觉上将没有任何迟滞，当然也可采用压缩时间轴，加快时间轴的运行速率来达到平滑的效果。本研究采用1帧/秒并且压缩时间轴来进行仿真。

利用本文介绍的轨迹点经纬度计算方法计算出航空器飞行轨迹上点的经纬度，导入KML中的关键标签便可以实现模拟航空器沿规定航线飞行的功能。如图2所示。

图2 动态显示截图

3 等待程序改出算法

飞行等待程序的加入算法参考潘卫军等人的飞行等待程序及仿真研究［1］，本文重点讨论等待定位点和IAF点在一条直线上的飞行等待程序的改出算法。

飞行等待程序改出方法1:平飞改出，直飞IAF点并下降至IAF点高度层;过IAF后沿原航向继续飞行并下降到IF点高度;按标准转弯率转弯飞往IF点处并切进近航向道真航向;平飞至FAF点，开始最后进近。

图3 等待程序改出算法流程图

飞行等待程序改出方法2:在等待程序中以标准下降率(1min下降600m)依次按高度层下降到IAF点高度层;平飞至IAF点;过IAF点后沿原航向继续飞行并下降到IF点高度;按标准转弯率转弯飞往IF点处并切进近航向道真航向;平飞至FAF点，开始最后进近。等待程序的改出流程如图3所示。

图3中的L1为飞机当前位置转到进近航向道所需飞行距离;L2为飞机从当前航向按照标准转弯率w转到目标航向所需飞行距离;TcQU为航空器当前位置点Q(eQ，nQ)与进近航向道上任意一点U(eU，nU)连线的相对真航向。在判断TcQU=Hap时，有种特殊情况需要注意，比如航空器的标准转弯率W为3°/s，当前航向为20°，Hap为22°，实际情况下航空器只需转动2°。为了解决这个问题，考虑到因为航空器转动到目标航向后接着做直线运动，所以从航向20°转到航向22°的过程中，在 W=3°/s的情况下只需2/3秒，剩下1/3秒的时间则用来做直线运动。所以在这种情况下，航空器在这一秒内的横纵坐标增量就是在新的转弯率下的转动增量加上直线运动增量。

下面讨论TcQU以及L1、L2这3个数学判断模型的确定:

由于所计算的飞行距离L1与L2是圆弧距离，所以首先计算转弯半径，由于按标准转弯率转弯的半径R已知，所以:

另设QU连线的大圆航线距离为SQU，计算L1的模型如下:

根据以上数学模型，按照图3的算法流程进行仿真，结合第1节给出的中航空器运动轨迹坐标模型，计算出航空器飞行轨迹经纬度坐标，就可以实现整个模拟仿真。2种改出方法的仿真结果分别如图4和图5所示。

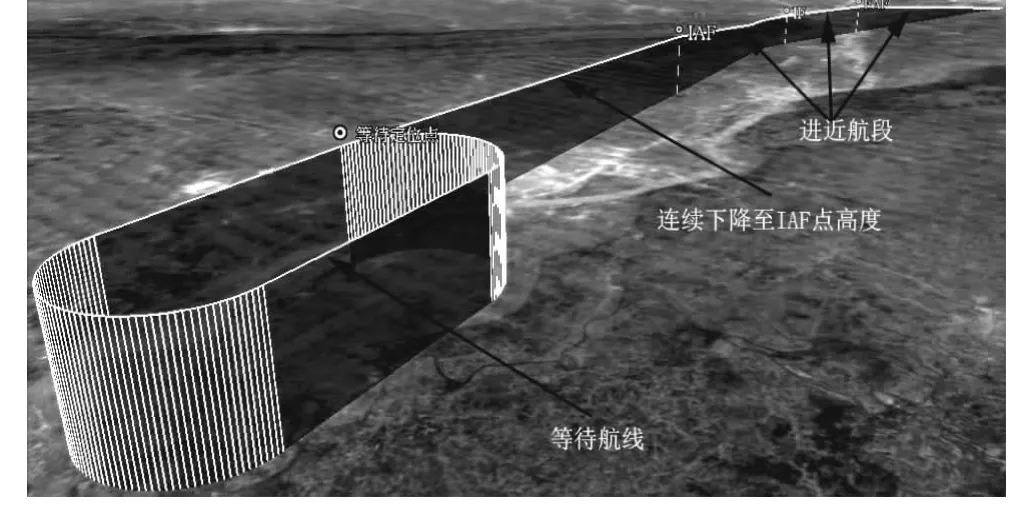
图4 飞行等待程序改出方法1

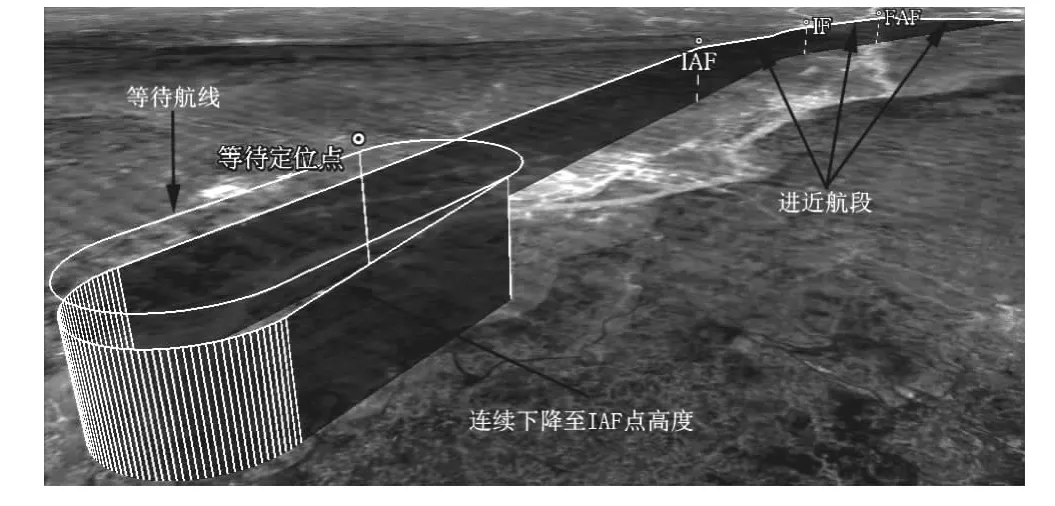
图5 飞行等待程序改出方法2

4 结束语

基于GE软件平台的飞行模拟技术采用免费的地理信息资源，方便、直观地实现航空器在飞行程序中的飞行流程和状态的三维仿真，给实际工作带来了便利。本研究重点分析了标准等待程序的改出算法，利用贝塞尔大地主题算法推算出航空器的各种运动状态下轨迹点经纬度坐标的计算模型以及改出算法中的判断模型，结合计算机编程和GE软件实现了飞行等待程序改出的三维仿真。今后将继续研究运用计算机编程语言调用GE提供的API，对KML文件进行自动化读取和写入，以实现更加自动化和人性化的三维飞行仿真界面。

［1］Google Developers.KML［DB/OL］.http://code.google.com/apis/kml，2005-12-09.

［2］OGC.KML［DB/OL］.http://www.opengeospatial.org/standards/kml/，2005-12-09.

［3］李夏.仪表飞行程序三维呈现系统设计的初步研究［D］.广汉:中国民用航空飞行学院，2011.

［4］潘卫军，陈文涛，刘璠.飞行等待程序及仿真研究［J］.航空计算技术，2008，38(6):50-53.

［5］唐勇，刘昌忠，吴宏刚.基于GoogleEarth的三维航迹监视及六自由度飞行仿真［J］.计算机应用，2009，29(12):3385-3387.

［6］卢敏.基于GIS的飞行程序设计［D］.北京:北方工业大学，2006.

［7］向硕凌.仪表飞行程序三维动态呈现技术研究［D］.广汉:中国民用航空飞行学院，2011.

［8］史国友，周晓明，贾传荧.贝塞尔大地主题正解的改进算法［J］.大连海事大学学报，2008，34(1):78-81.

［9］王瑞，纪兵，边少锋.地面上两点间方位角和距离计算的实用公式［J］.海军工程大学学报，2009，21(5):22-26.

［10］宋柯.空中交通流量预测与三维飞行仿真［J］.空中交通管理，2010(1):18-20.

［11］宋柯.三维航空图绘制方法初步研究及实现［J］.空中交通管理，2009(8):25-27.

［12］肖潇.GIS应用软件开发模式分析［J］.计算机与现代化，2007(9):51-53.