基于相位一致性和自适应极坐标变换的图像匹配方法

肖志涛，邱 虹，耿 磊，张 芳，吴 骏

（天津工业大学 电子与信息工程学院，天津 300387）

0 引言

图像匹配是指在变换空间中寻找一种或多种变换，使来自不同时间、不同传感器或不同视角的同一场景的两幅或多幅图像在空间上对准.图像匹配一般分为基于灰度相关和基于特征的匹配.前者对图像灰度变换和几何畸变等比较敏感，后者对图像灰度变化、形变和遮挡有较强的鲁棒性.目前，图像匹配已广泛应用到图像识别、图像分析和计算机视觉、目标识别等诸多领域.

近几十年来，图像匹配算法得到了迅猛发展.比如由Kuglin和Hines[1]提出了相位相关法（phasecorrelation method,PCM）.Averbuch和Keller Y[2]提出一种基于FFT的图像匹配算法，能够估计出亚像素精度的平移量.文献 [3]提出在频域求取图像间的平移与旋转量，利用图像的全部信息使得匹配精度高并且抗噪能力强，但在平移量较小或者图像裁剪的情况下匹配精度降低.Fourier-Mellin[4]变换先将图像变换到对数极坐标，再应用相位相关方法求得图像间的旋转、缩放和平移量.文献 [5]提出一种混合算法，先在空间域中使用对数极坐标技术作为预处理来恢复大尺度变换和任意旋转角度，然后通过使用非线性最小二乘优化实现亚像素精度.由于对数极坐标变换存在采样不均匀的问题，导致中心区域的过采样和边缘区域的欠采样，文献6提出自适应极坐标变换（adaptive polar transform，APT）方法，能够对图像进行均匀有效的采样.

在上述基础上提出一种采用相位一致性（phase congruency，PC）进行特征提取的自适应极坐标变换方法，本方法在图像间存在平移、旋转、尺度变换以及部分遮挡的情况下能够准确的进行匹配，并且具有亮度和对比度不变性.

1 自适应极坐标变换

1.1 自适应极坐标变换

对数极坐标变换（log-polar transform，LPT）是先对图像进行极坐标变换，再进行对数变换.图像在直角坐标系下的旋转和尺度变换在对数极坐标系中表现为平移.但由于LPT的采样不均匀，导致在图像中心区域过采样而边缘区域欠采样.

自适应极坐标变换[6]（adaptivepolar transform，APT）是将图像映射到极坐标系，与LPT不同的是，APT圆周方向的采样数不是固定不变的，而是随着极径值的增大而增加.因此，APT可以实现对整幅图像的均匀采样，使边缘区域的信息也能得到有效利用.

对于大小为2max×2max的图像，令 和 分别为极径和圆周方向的采样数.选取 =max，以 代表极径方向第 个采样点处的半径值.由于在半径 处，圆周方向的采样数大约为2 个像素，取 =8.设图像 , ，大小为2max×2max，进行APT

1.2 投影变换

为了使APT具有旋转和尺度不变性，要进行投影变换，对变换后的图像分别进行极径和角度方向的投影.

对于大小为2max×2max的图像 , ，进行APT变换后的图像为 , ，设 和 分别为极径方向和角度方向的投影，有

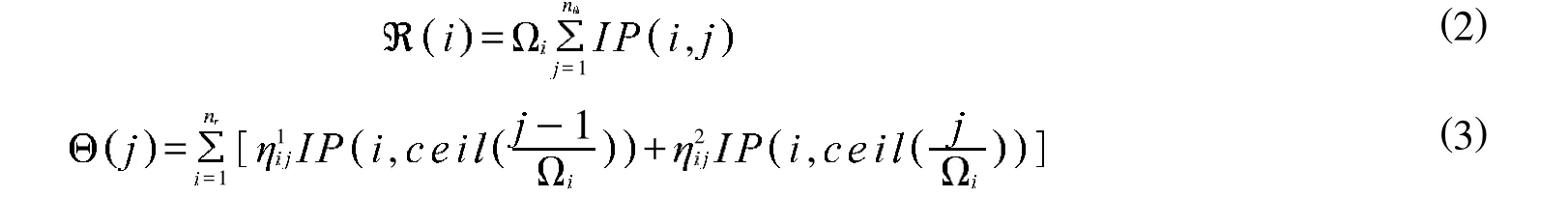
式中： 1,, ， 1,, ，= ，1= 1 1 ，2=11. 表示在 =max处圆周方向的采样数， 表示大于或等于 的最小整数，表示小于或等于 的最大整数.

图1为将图像进行投影变换的结果.图中虚线表示原图的投影，实线表示旋转或尺度变换图像的投影.可以看出，对于仅存在旋转的图像，在极径方向上的投影几乎重合，而在角度方向上的投影表现为平移；对于仅存在尺度变换的图像，在角度方向上的投影重合，而在极径方向上的投影不同.因此，求图像的旋转量只需要考虑角度方向投影，而图像的尺度变换量只需要考虑极径方向的投影.

2 基于自适应极坐标变换（APT）的图像匹配

本文首先确立参考图像和目标图像组.先对模型图像使用相位一致性和非极大值抑制确定非极大值抑制值较大的点为中心点，以中心点为圆心、以 为半径的圆片作为参考图像.对目标图像也使用相位一致性和非极大值抑制提取特征点，以每一个特征点为圆心、以 为半径的圆片作为目标图像组.再次使用相位一致性对参考图像和目标图像组的每幅图像进行特征提取.然后变换到自适应极坐标，通过分别计算极径方向和角度方向的投影得出图像间的尺度和旋转变换量.最后应用欧式距离公式找寻最小值定位出参考图像的中心点在目标图像中的位置完成最终的图像匹配.

2.1 利用相位一致性进行特征提取

相位一致性[7]（phase congruency，PC）是一种特征检测方法，它是由Morrone等[8]人通过对马赫带现象的研究提出来的.PC处理结果不受亮度和对比度的影响，具有通用性、稳健性，并且与人类视觉感知特性一致.

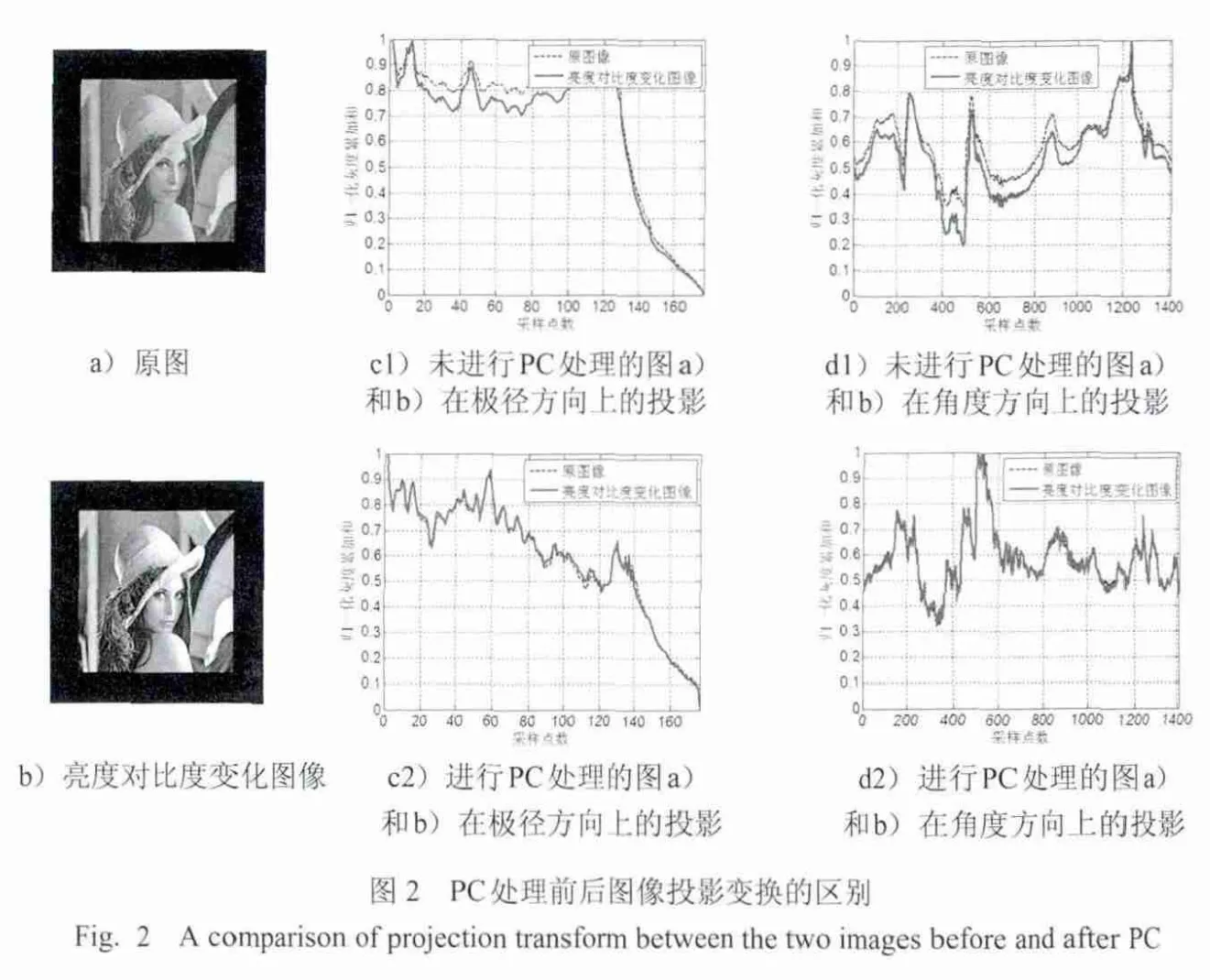
图2为图像亮度和对比度改变时，对PC处理前后的图像进行投影变换的区别.图中虚线表示图2a）的变换曲线，实线表示图2b）的变换曲线.可以看出，对图像进行PC处理的投影曲线几乎重合，而未对图像进行PC处理的投影曲线具有差异性.由于后续需要应用投影变换求图像的旋转和尺度参数，而PC对亮度和对比度具有鲁棒性，所以对图像先进行PC处理可以提高匹配的准确性.

2.2 基于APT的图像匹配

在极坐标域，上式可以表示为

先计算图像的尺度参数，将图像的尺度恢复后再计算其旋转参数，最后进行定位来达到图像匹配的目的．

2.2.1 计算尺度参数

由图1可以得出求图像的尺度参数只需要考虑在极径方向上的投影．根据式 (2)可以计算出参考图像和目标图像在极径方向上的投影，如下所示

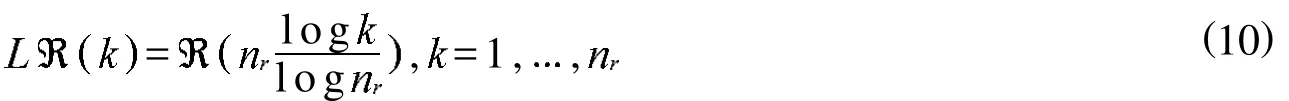
2.2.2 计算旋转参数

计算出尺度参数后，将图像按照尺度因子变换回去再计算旋转参数．根据式 (3)可以得出参考图像和目标图像在角度方向上的投影，如下所示

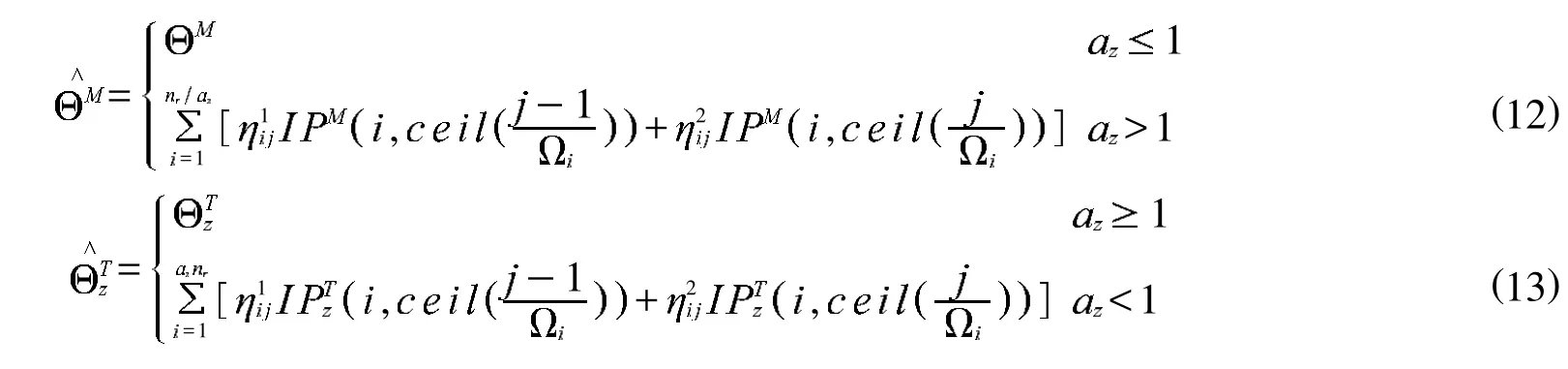
由图1可以看出图像的旋转参数在极径方向上的投影表现为平移，因此求得平移量就可以求得图像的旋转参数．本文对和进行归一化，找其最高点之间的平移量，根据得到旋转量．

2.2.3 定位

得到参考图像和目标图像组的尺度和旋转参数后进行定位．对参考图像 和目标图像的投影和应用欧式距离可得

3 实验结果与分析

为了验证本文所提出方法的有效性，对存在旋转、尺度变换、亮度对比度变化以及部分遮挡的情况下的图像进行实验，并与现有方法进行了比较．图3为本文所使用的参考图像，图3a）为采集的模型图像，图3b）圆圈内图像则为参考图像．

图3 模型图像与参考图像Fig.3 Model imageand reference image

1）目标图像相对于参考图像只存在旋转．图4a1）～图4c1）为本文方法匹配结果，图4a2）～图4c2）为文献 [6]方法的匹配结果，表1为具体数据．可以看出，本文方法和文献 [6]方法对存在旋转的图像都可以准确匹配．

2）目标图像相对于参考图像只存在尺度变换．图5a1）～图5c1）为本文方法匹配结果，图5a2）～图5c2）为文献 [6]方法的匹配结果，表2为具体数据．可以看出，本文方法和文献 [6]方法对存在尺度变换的图像都可以准确匹配．

3）目标图像相对于参考图像同时存在旋转、尺度变换以及部分遮挡．图6a1）～图6c1）为本文方法匹配结果，图6a2）～图6c2）为文献 [6]方法匹配结果，表3为具体数据.可以看出，本文方法和文献 [6]方法都可以对同时存在旋转、尺度变换以及部分遮挡的图像准确匹配.

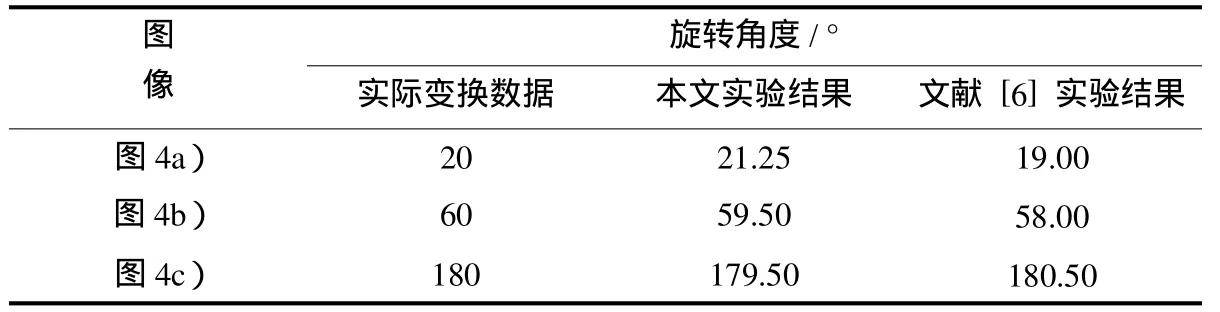
表1 只存在旋转时的匹配结果Tab.1 The imagematching resultsof rotation

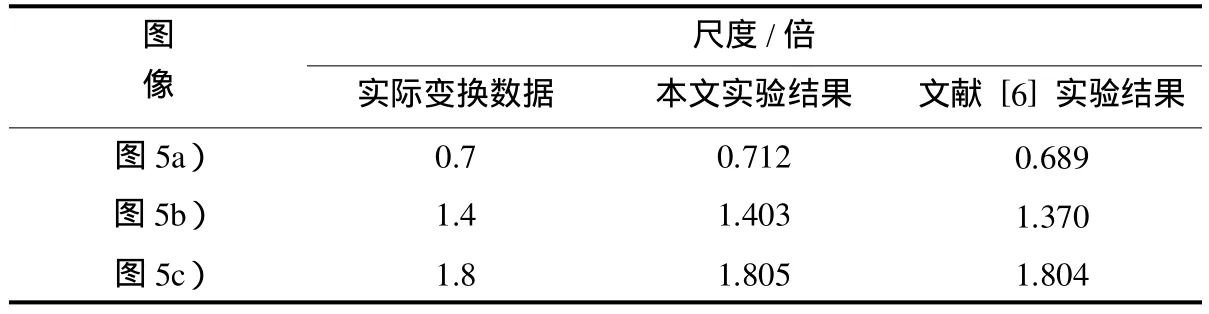
表2 只存在尺度变换的匹配结果Tab.2 The imagematching resultsof scaling transformation

图4 旋转图像的匹配Fig.4 Rotated imagesmatching

图5 尺度变换图像的匹配Fig.5 Scaled imagesmatching

表3 同时存在旋转、尺度变换以及部分遮挡的匹配结果Tab.3 The image matching results of rotation,scaling transformation and partialocclusion

4）目标图像相对于参考图像存在亮度、对比度变化.图7a1）～图7d1）为本文方法匹配结果，图7a2）～图7d2）为文献 [6]方法匹配结果，表4为具体数据.实验表明，当图像亮度增加超过40%或减少20%、对比度增加超过60%或减少20%时，文献 [6]方法无法正确定位，匹配出错.这是由于图像亮度、对比度的变化增大时导致投影变换曲线变化增大，使用相关函数计算时误差增大，无法正确匹配.而本文方法采用的相位一致性具有亮度和对比度不变性，当图像亮度、对比度增加或减少到80%时仍能正确匹配.

表4 存在亮度、对比度变化的匹配结果Tab.4 Matching results of imagesw ith brightness and contrast changes

综上所述，本文方法对图像间存在旋转、尺度变换以及部分遮挡情况下的图像能够准确匹配，其误差与文献 [6]数据相当.但图像间存在亮度和对比度变化的情况下，本文方法比文献 [6]更能准确匹配图像.

4 结论

本文研究了图像间存在旋转、缩放、平移、亮度和对比度改变以及部分遮挡情况下的图像匹配.首先使用相位一致性对参考图像与目标图像进行特征提取，然后进行自适应极坐标变换，最后通过计算投影变换得出旋转与尺度变换参数并对图像进行匹配.自适应极坐标变换克服了对数极坐标存在的采样不均匀的问题，当图像存在遮挡的情况下也能准确匹配.而相位一致性对图像亮度和对比度变化具有鲁棒性.实验结果表明，在图像间存在平移、旋转、尺度变换以及部分遮挡的情况下能够精确匹配，并且具有亮度和对比度不变性.

[1]Kuglin CD，HinesDC.The phasecorrelation imagealignment method[J].IEEE International Conferenceon Cybernetics and Society，1975：163-165.

[2]Averbuch A，Keller Y.FFT based image registration[J].IEEE International Conference on Acoustics，Speech，and Signal Processing，2002，4：3608-3611.

[3]Lucchese L，Cortelazzo GM.A aoise-robust frequency domain technique for estimating planar roto-translations[J].IEEE Transactionson Signal Processing，2000，48（6）：1769-1786.

[4]Zhang J，Ou Z，Wei H.Fingerprint matching using phase-only correlation and fourier-mellin transforms[J].IEEE International Conference on Intelligent Systems Design and Applications，2006，2：379-383.

[5]Zokai S，Wolberg G.Image registration using log-polar mappings for recovery of large-scale sim ilarity and projective transformations[J].IEEE Transactionson Image Processing，2005，14（10）：1422-1434.

[6]Matungka R，Zheng Y F，Ew ing R L.Image registration using adaptive polar transform[J].IEEE Transactionson Image Processing，2009，18（10）：2340-2354.

[7]Logesparan L，Rodriguez-Villegas E.A novelphase congruency based algorithm for online data reduction in ambulatory EEG systems[J].IEEE Transactionson Biomedical Engineering，2011，58（10）：2825-2834.

[8]KovesiP.Image features from phase congruency[J].Journal of Computer Vision Research，1999，1（3）：1-26.