Runge-Kutta法在微分方程初值问题中的应用

2014-10-13郭志萍

太原城市职业技术学院学报 2014年2期

关键词：级数方程组二阶

郭志萍

（浙江工业大学化材学院，浙江杭州 310014；山西水利职业技术学院，山西运城 044004）

Runge-Kutta法在微分方程初值问题中的应用

郭志萍

（浙江工业大学化材学院，浙江杭州 310014；山西水利职业技术学院，山西运城 044004）

本文利用Taylor级数推导了二阶Runge-Kutta算法，并得到了经典的四阶Runge-Kutta法。结合Matlab语言，在微分方程的初值问题中应用Runge-Kutta法数值计算了一阶微分方程和高阶微分方程组。Runge-Kutta法能够较高精度地数值模拟数学建模所建立的微分方程。

Runge-Kutta法；Matlab；微分方程；数值计算

一、引言

微分方程是自然科学和社会科学研究中非常重要且十分实用的一种数学工具。Runge-Kutta法是一类具有相当实用价值的方法，也是最常用的一种数值方法。在数值求解微分方程初值问题中应用广泛,张鹏利对两空泡的共振频率,共振振幅及空化噪声声压利用Runge-Kutta法进行了数值求解；Runge-Kutta法在振荡电路求解中的应用；淹没磨料射流的运动分析，等等。应用Runge-Kutta法来数值求解，能够较高精度地数值模拟数学建模所建立的微分方程，其计算与实验结果吻合较好。这种方法能够解决的问题越来越多，越来越复杂，在微分方程数值求解方法中扮演着非常重要的角色。

Matlab的基本单位是矩阵，它的表达式与数学、工程计算中常用的形式十分相似，极大地方便了人们学习和使用。利用Matlab提供各种数学工具，可以避免做繁琐的数学推导和计算，方便地解决了很多数学问题。

本文从理论上对Runge-Kutta法进行了推导，运用Matlab语言，在具体的微分方程初值问题算例中详细地给以求解。

二、初值问题数值解

除常系数线性微分方程可用特征根求解，少数特殊方程可用初等积分法求解外，大部分微分方程无显式解，应用中主要靠数值解。考虑一阶常微分方程组初值问题：

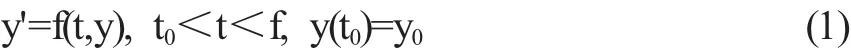
其中 y=(y1,y2,L,ym)T，f=(f1,f2,L,fm)T，y0=(y10,y20,L,ym0)T，这里表示转置。所谓数值解，就是寻求y(t)在一系列离散节点t0＜t1＜L＜tn〈tf上的近似值 yk(k=0,1,L,n)。称 hk=tk+1-tk为步长，通常取为常量h。

高阶的常微分方程初值问题可以化为一阶常微分方程组，已给一个n阶方程：y(n)=f(t,y,y',L,y(n-1))T

设y1-y,y2=y',y1-y,L,yn=y(n-1),式(9)化为一阶方程组：

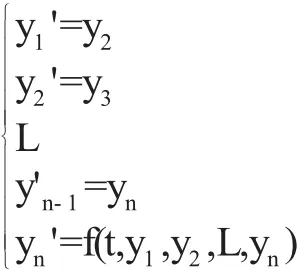
三、Runge-kutta法推理过程

Runge-kutta方法是一种单步法，是用函数f在tk和tk-1之间值的有限差分近似代替高阶导数。下面以二阶为例来推导：Taylor级数

中多保留一项，可得到二阶Taylor级数法

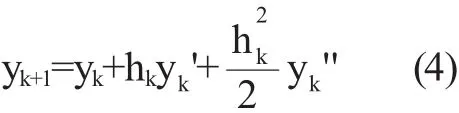
通过链式法对求导，即

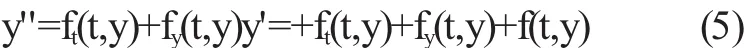
其中的下标表示的是给定变量求偏导。

由此得到

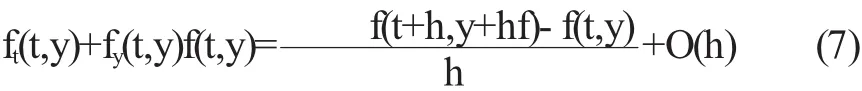
用上式近似二阶导数，得到Runge-Kutta法

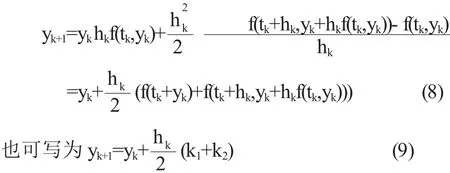
其中 k1=f(tk,yk)，k2=f(tk+hk,yk+hkk1)

Runge-kutta方法优点：计算tk+1时刻的值时，并不需要tk时刻以前的值。

最著名的是四阶经典的Runge-kutta格式

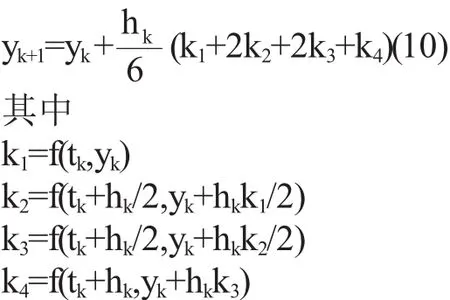
四、Runge-Kutta方法在Matlab语言中的应用

下面以常用的ode45为例讲解：

其调用格式为：[t,y]=ode45(odefun,tspan,y0)其中，odefun为用以表示的函数句，为标量，y为标量或向量；tspan如果是二维向量[t0,tf]，表示自变量初值和终值；如果是高维向量[t0,t1,…,tn]，则表示输出节点列向量；y0表示节点列向量t=(t0,t1,L,tn)T；y表示数值解矩阵，每一列对应y的一个分量；若无输出参数，则作出图形。

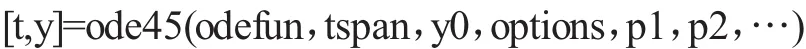
其中，options为计算参数，默认可用空矩阵[]表示；p1,p2,…为附加传递参数，这时odefun的表示为f(t,y,pl,p2,L)。

运行程序输出和的关系。

Runge-kutta法有利于解决数学中的许多实际微分初值问题，方便、易操作，而且图像处理清晰明了。Runge-kutta法是联系数学与实际问题的桥梁，能够较高精度地数值模拟数学建模所建立的微分方程，其计算与实验结果吻合较好。这种方法能够解决的问题越来越多，越来越复杂，在微分方程数值求解方法中扮演着非常重要的角色。