海洋平台抛锚方式模糊优化设计方法
2014-10-11霍发力杨德庆
霍发力,杨德庆
(上海交通大学船舶海洋与建筑工程学院海洋工程国家重点实验室,上海 200240)
石油是国民经济的血脉,拥有充足的油气资源,并且保证油气资源的稳定供给,是经济平稳发展必不可少的前提保障。目前海洋油气的开发已由近海浅水向远海深水发展。深海石油资源开发平台大多由三个部分组成:浮体结构、锚泊定位系统和立管。浮体通过锚泊定位系统长期固定于特定海域,通过立管输油进行石油的开采工作,这就决定这些浮式系泊系统的设计要经受得住恶劣的波浪、流及风等随机环境载荷的作用。在锚泊定位系统的设计中,正确确定其在海洋环境载荷作用下的运动响应及系泊缆绳张力显得十分重要。
关于锚泊设计优化,国内外做了大量研究。Mehdi Shafieefar[1]提出了一种基于遗传算法对浮式平台锚泊系统的锚链布局和锚链张力等的优化设计自动程序。通过这种方法可以快速找到使平台响应最小的最好的锚泊系统。Rio de Janeir[2]发展了一种利用遗传算法解决锚泊系统布置的优化问题。此方法优化了锚泊布置使得平台漂移量达到最小。Fylling I[3]等对深水半潜平台的锚泊系统优化设计进行了大量研究。Matthias Brommundt[4]在时域内对海上半潜式风力发电设备的悬链线式锚泊系统进行了优化设计,运用Nelder-Mead单一算法来优化锚链长度即锚泊系统成本达到最优。余龙等[5]运用准静定方法对多成分锚链进行了优化设计,基于准静定方法推导限定水深下多成分锚泊线悬链线方程,并考虑锚泊线组成成分的参数对锚泊系统回复力的影响,建立目标函数最小化的多成分锚泊线优化设计模型,来设计多成分锚链的锚泊系统。张火明和杨建民[6]等基于一维优化思想,运用黄金分割法和悬链线方程方法研究了多成分系泊缆索静力特性计算方法。
在实际工程中,海洋平台的设计要满足船级社对平台锚泊系统设计分析的最低要求。根据API与ABS规定[7-8],在钻井工作工况下,应满足最大轴向拉力低于破断强度的44.4%,并且由于直接与钻井立管的球形连接点角度要求,平台水平偏移根据钻井系统要求在水深的5%以内,以防止损坏钻井立管以下的球形接头内的机械止动器。在风暴工况下,由于立管与平台脱离,水平漂移量没有具体要求,而要求锚链轴向张力不超过破断强度的60%。在保持抛锚点与锚链出缆位置一定情况下,随着系泊链长度的增加,锚链轴向张力的最大值呈现先减小后增大的趋势。而对于钻井工况,一般处在端部张力随锚链长度增加而减少的阶段,在这阶段中,随着锚链的增长,锚链端部张力虽然相应减少,但是漂移量会相应增加。这就要求在满足水深5%漂移量的前提下,尽量减少锚链端部张力,从而可以提高锚链的疲劳寿命,来增加锚链安全使用年限。而对于风暴自存工况,所处环境非常恶劣,这就要求锚链轴向张力尽量减少,从而增加平台锚链的安全余量。所以根据抛锚长度的增加,锚链端部张力的变化趋势,找到轴向张力最小处的抛锚长度,可以提高平台锚泊系统的安全余度,增加平台抗风暴强度的能力。
针对深海半潜式平台及其系泊系统,运用平台与锚链耦合运动时域分析方法,对钻井平台及其悬链线式系泊系统的水动力性能进行探索,提出一种基于模糊方法的锚泊系统抛锚方式优化设计方法,此方法能使钻井平台在风暴自存工况和钻井工作工况,较快找到最佳抛锚方式。以一典型半潜式钻井平台为例进行数值模拟,结果表明本文提出的方法是可行的,能够方便地找到较好的抛锚方式,锚链最大轴向张力和平台平面漂移量均能够满足规范要求。
1 模糊优化设计
模糊控制是以模糊集合论、模糊语言变量及模糊逻辑推理为基础的一种计算机数字控制[9-10]。模糊控制从线性控制与非线性控制的角度分类,是一种非线性控制;从控制器的智能性看,模糊控制属于智能控制的范畴,而且它已成为目前实现智能控制的一种重要而又有效的形式,应用潜力很大。模糊控制理论的研究和应用在现代控制领域中具有重要的地位和意义。
1.1 模糊方法控制系统参量及参量的模糊化
为设计一个优良的模糊方法控制器,其关键是要有一个便于灵活调整的模糊规则。基于解析表达式的模糊数模型就具有这样的优点。
双输入单输出模糊方法控制器的方框图如图1所示。模型结构所涉及的3个语言变量是:误差E、误差变化EC和控制量的变化U。
1.2 建立模糊方法数模型

图1 双输入单输出模糊控制器Fig.1 The fuzzy controller of double-input and single-output
设计优良的模糊方法,其关键是灵活调整的模糊规则。基于解析表达式的模糊方法数模型具有这种优点,根据海洋平台锚泊系统分析规范要求,设计了风暴自存工况和工作工况下的模糊方法控制器。
1.2.1 风暴自存工况
对于风暴自存工况的双输入单输出模糊方法控制器所涉及的3个语言变量是:误差E为锚泊系统中的端部最大轴向张力与锚链破断强度比值,误差变化EC为抛锚长度改变后端部最大轴向张力的变化量,控制量的变化U对应抛锚长度变化ΔL。
对于风暴自存工况,模糊数模型的结构可采用下列解析式来表达:
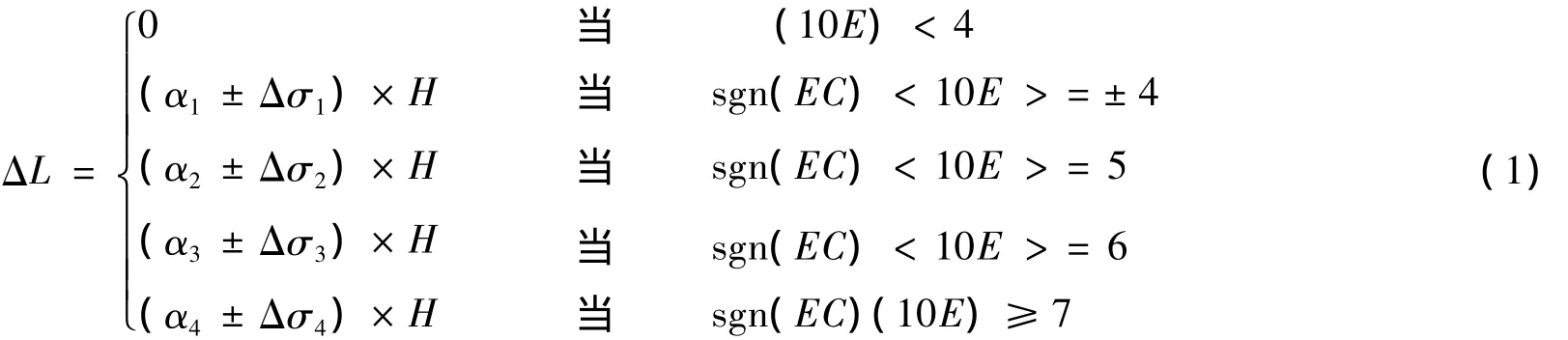
其中,αi和Δαi为修正因子,sgn为符号函数,< >为取整符号,H为ΔL初步变化常数。使用修正因子使控制规则的修改更加灵活,可以改变修正因子来满足系统在不同状态下的要求。模糊方法优化步骤如下:
1)当初始锚链长度设置为L,计算出锚链端部最大轴向张力;
2)然后改变锚链长度为L+H,再计算出锚链端部最大张应力;
3)根据此情况下锚链端部最大轴向张力与破断强度比值E,抛锚长度改变后端部最大轴向张力的变化量EC,判断E处于式(1)中的哪个阶段,来确定下一步优化时的锚链长度。
4)重复步骤2)与3),最终在ΔL=0时终止。
1.2.2 钻井工作工况
对于工作钻井工况的双输入单输出模糊方法控制器所涉及的3个语言变量是:误差E为船体最大偏移量与允许船体漂移量比值,误差变化EC为抛锚长度改变后船体漂移量的变化量,而控制量的变化U即对应抛锚长度变化量ΔL。

式中:相关符号含义和分析步骤如式(1)所示。此数学模型是从锚链抛锚长度等于锚链出缆点与抛锚点距离开始进行优化。为了能够尽快找到最优点,可以在此基础上加上一定长度开始进行。
2 浮式系泊系统时域内平台与锚链耦合运动
随着半潜式平台向深海发展,为准确预报平台运动响应,必须充分考虑系泊系统的粘性效应、惯性质量、流载荷和回复力。传统的动力响应分析是将浮体、缆绳和立管独立开来,分别进行计算,在精度方面存在很大误差[22]。Kanda[12]和Ma[13]通过对一TLP平台的研究证明,浮体及管线的相互作用会对浮式结构的动力响应带来很大的影响。Kim等[14]对TLP平台进行非耦合分析,证明其精度随着水深的增加而降低;Bauduin,Blanc等[15]通过大量的模型试验数据来校准时域分析方法中的相关系数,从而提高分析精度;Zou,J等[16]通过对现役的多个张力腿平台的耦合情况进行测试研究,对耦合分析进行了改进。Wang Li-zhong[17]运用准静态法考虑了耦合效应,对吸力锚泊系统在水和土壤部分联合分析。Ying MinLow[18]运用船体和锚链的耦合效应进行锚链的疲劳分析。
平台响应和系泊系统响应不应单独求解,而应将系泊系统和平台系统整体考虑为动态系统联合求解。DNV研发的船舶与海洋结构物分析软件SESAM功能强大,其DeepC模块专门针对平台整个系统的耦合问题进行求解,是海工领域内认可的能够较好解决此问题的软件。对于平台系泊系统时域内的耦合运动方程可以写成[19-20]:


式(4)与式(5)中,下表V和L分别表示浮体与系泊缆索,表示系泊缆索受到的外力。

式中:T和Q分别为轴向和旋转方向的恢复力,W为系泊缆索单位长度的有效重量,FS表示系泊缆索受到的来自连接锚的力。
Fm表示结构上的总的波浪力:拖拽力及惯性力,由莫里森方程可知:
盐城市区饮用水源生态净化工程库区生态堤防设计……………………………… 朱冬舟,陆惠萍,仓基俊等(14.26)
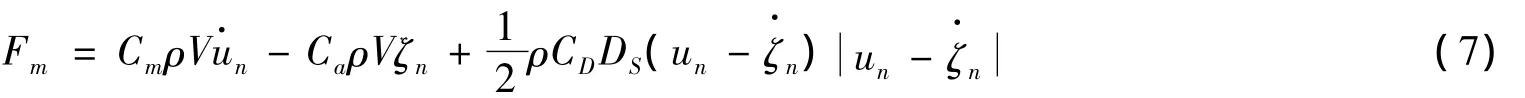
式中:V=πD2/4为细长结构在单位长度上的体积,D为结构的直径。Cm=1+Ca为惯性系数,Ca为附加质量系数,CD为拖拽力系数,DS为结构物的直径或者宽度n和un分别表示流体的加速度和速度沿浮体外表面的法向分量,和分别表示浮体运动的加速度和速度。
浮体的质量矩阵MV包含两个部分:浮体结构质量矩阵及其由辐射势产生的附加质量矩阵;浮体阻尼矩阵BV包含三个部分:粘性阻尼矩阵、慢漂阻尼矩阵以及由辐射势产生的附加阻尼矩阵;KV为浮体的线性水动力刚度矩阵。对于系统的运动微分方程,可以采用Wilson-θ隐式方法积分求解,这是线性加速度方法的推广[21]。
3 半潜平台基本数据及环境参数
以工作于中国南海某半潜钻井平台为例,进行数值模拟优化分析。平台的主要参数如表1和表2所示。平台的工作、风暴和拖航工况下吃水(重量)分别为:23.38 m(23 598 t)、17.32 m(20 187 t)和10.90 m(17 895 t)。根据平台锚泊定位操作手册中提到的环境工况如表3所示。

表1 半潜平台主要参数Tab.1 The parameters of semi-submersible platform

表2 锚泊系统主要参数Tab.2 The parameters of mooring system
根据平台锚泊定位操作手册规定的锚链出链角度方式如图2所示。

表3 环境参数Tab.3 The parameters of condition

图2 锚泊抛锚方式Fig.2 Mooring anchor method
4 锚泊系统优化分析
依据船体与锚链的时域耦合计算方法,运用DeepC/SESAM软件,在出缆点与抛锚点位置一定,只改变抛锚长度的情况下,根据表3中提到的风暴自存工况,对此半潜钻井平台进行数值模拟。风、浪和流均来自0°方向,计算锚链长度为2 200~2 800 m,每间隔50 m共13种情况。结果如图3所示。
由图3可以看到,锚链端部最大张力先减少后增加,而且变化趋势开始时轴向张力减少非常块,在接近最小处附近变化趋势变得很缓慢,然后开始增加,而且增大趋势变快。这是由于在保持出链点与抛锚点一定的情况下,在抛锚长度的增加过程中,初始时随着系泊链长度的增加,整个系泊系统的张紧趋势逐渐缓减,系泊链将处于更加放松的悬链状态,张力的最大值自然能够得到适当的降低;而当长度增加到一定值时,系泊链的自重增加将会十分显著,此时由于自重增加而造成系泊链张力上升的因素将起主导作用,即此后随着链长度的增加,上端张力的最大值不断增加。综合来说,系泊链上端张力的大小变化取决于链的张紧状态和自重两个因素,当其中一个因素占据主导地位时,其值就会发生相应的变化[22]。
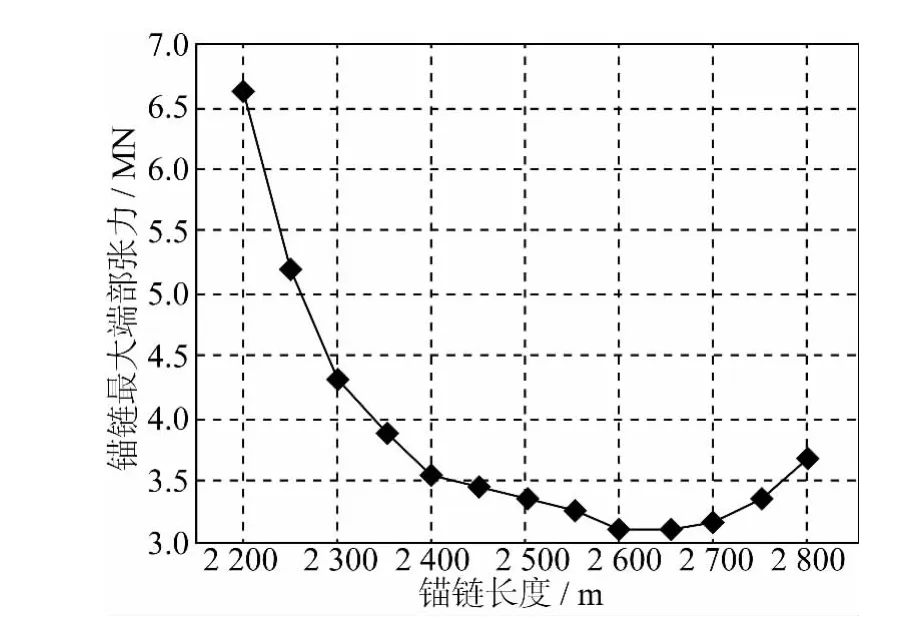
图3 锚链抛锚长度与锚链端部最大轴向张力Fig.3 The length of chain and the maximun axial tension
4.1 风暴自存工况抛锚方法优化设计
对于恶劣的风暴自存工况,要求设计出最佳的抛锚方式,即最优的锚链长度使得锚链轴向张力最小,可以大大提高平常的安全系数,相应增加平台的抗风暴能力。
本次优化设计变量为锚链抛出长度的增加量ΔL,根据模糊方法控制数学模型(8)进行设计优化。

式中相关符号含义如式(1)所示。
优化目标为锚链端部张力最小,即变量E达到最小。
根据规范要求,限制条件为:
1)设计锚链长度要小于平台现有锚链长度;
2)锚链端部最大轴向张力小于锚链破断强度的60%。
为了加快优化速度,锚链长度初步设计为出链点与锚泊点之间距离加上水深的10%(100 m)开始进行优化设计,其中H为水深的0.5%(5 m)。图4表示了锚链端部最大轴向张力的优化过程,图5表示了锚链长度的优化过程。经过优化设计可知,锚链端部最大张力先减少后增加,当锚链长度为2 595 m时,锚链端部最大张力为最小,最小值为3 076 650 N,为锚链破断强度的47.94%,小于锚链破段强度的60%,满足规范要求,锚链有很高的安全余量。图6~图8中给出了三种抛锚方式情况下,最大受力锚链端部轴向张力在时域中的变化情况。

图4 锚链端部最大张力优化过程Fig.4 The optimization history of the maximum axial tension

图5 锚泊出链长度优化过程Fig.5 The optimization history of chain length

图6 抛锚2 200 m时锚链端部最大张力在时域中示意Fig.6 The maximum axial tensions about 2 200 m of chain in time domain

图7 抛锚2 595 m时锚链端部最大张力在时域中示意Fig.7 The maximum axial tensions about 2 595 m of chain in time domain
4.2 钻井工况抛锚方法优化设计
在钻井工作工况下立管与船体相连,根据平台钻井系统的要求,为保证钻井能够在设计的钻井工况下照常工作,船体的漂移量不能超过水深的5%。在出链点与抛锚点一定的情况下,随着锚链长度的增加,船体漂移量增加,但锚链所受轴向张力相应减少,对于锚链的疲劳非常有益。所以在满足船体漂移量为水深的5%范围条件下,尽量减少锚链张力,以提高锚链的使用寿命。
本次优化设计变量为锚链长度的变化量ΔL,根据模糊方法控制数学模型(9)进行设计优化。
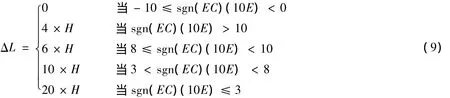
式中相关符号含义如式(1)所示。
优化目标为锚链端部张力最小,即变量E达到最小。
根据规范要求,限制条件为:
1)设计锚链长度要小于平台现有锚链长度;
2)锚链端部最大轴向张力小于锚链破断强度的44.4%;
3)船体水平漂移量小于水深的5%。
锚链长度初步设计为出链点与锚泊点之间距离加上水深的10%(100 m)。根据模糊方法控制理论,其中H为水深的0.5%,进行优化分析。图8表示了船体漂移量的优化过程,图9表示了锚链长度的优化过程,图10表示锚链端部最大轴向张力的优化过程。经过优化设计可知:当锚链长度为2 340 m时,漂移量为X轴:48.13 m,Y轴:2.86 m,水平漂移量48.21 m,为水深的4.824%,漂移量小于水深5%的要求;锚链轴向张力相应最小,端部最大张力为:2.508×106N,为锚链破断强度的39.084%,小于锚链破断张力的44.4%,满足ABS规范要求。图11~图12中给出了三种抛锚方式情况下,最大受力锚链端部轴向张力在时域中变化情况。

图8 船体偏移量优化过程Fig.8 The optimization history of vessel offset

图9 抛出锚链长度优化过程Fig.9 The optimization history of chain length

图10 锚链端部最大轴向张力优化过程Fig.10 The optimization history of maximum axial tension

图11 抛锚2 200 m时锚链端部最大张力在时域中示意图Fig.11 The maximum axial tensions about 2 200 m of chain in time domain
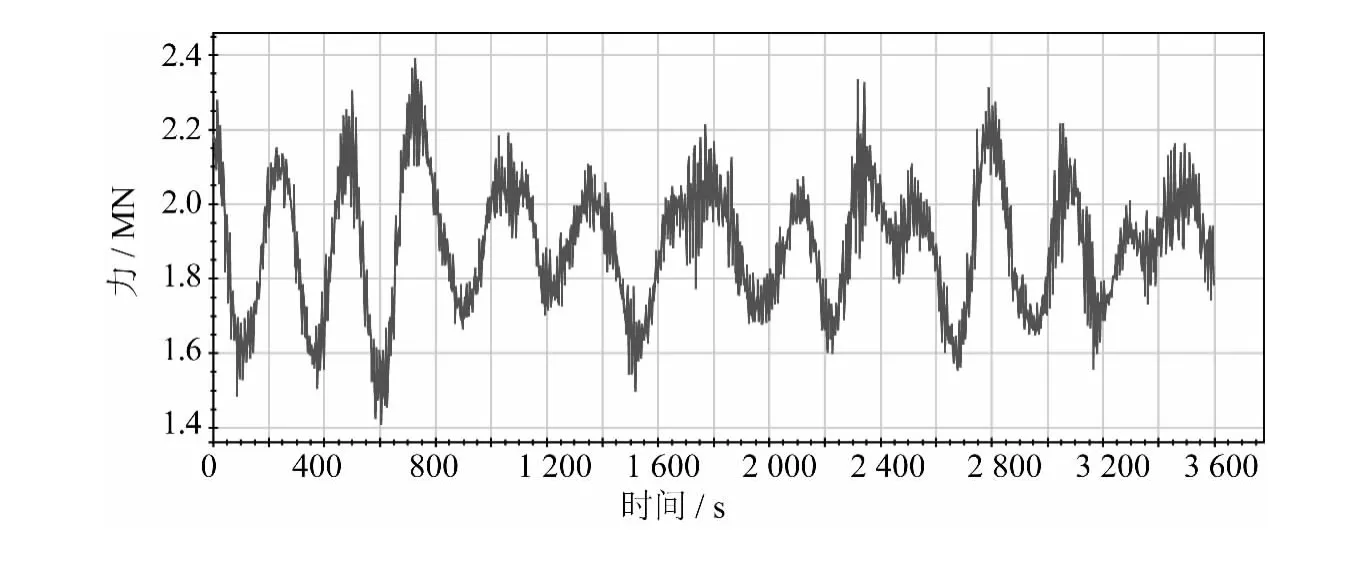
图12 抛锚2 340 m时锚链端部最大张力在时域中示意图Fig.12 The maximum axial tensions about 2 340 m of chain in time domain
5 结语
通过平台和锚链耦合运动系统时域分析,对深海平台进行动力响应特性和锚链强度分析,并根据其特性,利用模糊方法,分别针对钻井工作工况与风暴自存工况,提出了相应的优化设计方法。以位于中国南海水域某半潜平台为算例,对抛锚方案进行优化设计数值模拟。结果表明,设计的模糊方法控制抛锚方式优化方法是可行有效的,优化效果非常明显,能够很快地接近最佳抛锚方式。风暴自存工况下,锚链端部轴向张力最小为3 076 650 N,满足规范要求。钻井工作工况下,在满足船体漂移量为水深5%范围内,锚链轴向张力最小,端部轴向张力为2.508×106N,两种工况均能很好地满足ABS和API规范要求。
[1] Mehdi Shafieefar,Aidin Rezvani.Mooring optimization of floating platforms using a genetic algorithm[J].Ocean Engineering,2007(34):1413-1421.
[2] Alonso J,Juvinao Carbono,Ivan F M,et al.Mooring pattern optimization using genetic algorithms[C]//6th World Congresses of Structural and Multidisciplinary Optimization.2005.
[3] Fylling I.Optimization of deepwater mooring systems[C]//Proceedings of the Offshore Mediterranean Conference.1997.
[4] Matthias Brommundt,Ludwig Krause,Karl Merz,Mooring system optimization for floating wind turbines using frequency domain analysis[J].Energy Procedia,2012(24):289-296.
[5] 余龙,谭家华.基于准静定方法的多成分锚泊线优化[J].海洋工程,2005,23(1):69-73(YU Long,TAN Jia-hua.Research on optimum multi-component mooring lines based on catenary equation[J].The Ocean Engineering,2005,23(1):69-73.(in Chinese))
[6] 张火明,张晓菲,杨建民,基于优化思想的多成分系泊缆静力特性分析[J].舰船科学技术,2010,32(10):114-121.(ZHANG Huo-ming,ZHANG Xiao-fei,YANG Jian-min.Static characteristic analysis of multi-component mooring line based on optimization thinking[J].Ship Science And Technology,2010,32(10):114-121.(in Chinese))
[7] API RP2SK,Design and analysis of station keeping systems for floating structures[S].2005.
[8] ABS,Rules for building and classing mobile offshore drilling units[S].Part 3,2012.
[9] Ayhan Mentes,Ismail Hakki Helvacioglu.Fuzzy decision support system for spread mooring system selection[J].Expert Systems with Applications,2012,39:3 283-3 297.
[10]霍发力,曲鹏翔.导管架式海洋平台的MRFD半主动模糊控制理论研究[J].中国海洋平台,2010,25(2):39-44.(HUO Fa-li,QU Peng-xiang.Research of MRFD semi-active fuzzy control theory of jacket offshore platforms[J].China Offshore Platfrom,2010,25(2):39-44.(in Chinese))
[11] Ward E G,Haring R E,Devlin P V.Deep water mooring and riser analysis for depths to 10,000 feet[C]//Offshore Tech.Conf..1999.
[12] Kanda M,Mlyajima Nakagawa H,Shimazaki K.A non-linear coupled response of TLP hull and tendons in waves[C]//OMAE 98.1998:OMAE98-0472.
[13] Ma W,Lee M Y,Zou J,et al.Deepwater nonlinear coupled analysis tool[C]//OTC12085.2000.
[14] Kim M H,Tahar,A,Kim Y B.Variability of TLP motion analysis against various design methodologies/parameters[C]//ISOPE’01.2001:467-473.
[15] Bauduin C,Blanc C,Elholm E,et al.Erha deepwater export system coupled analysis and model test calibration[C]//Deep Offshore Technology(DOT)Conference.New Orleans:[s.n.],2004.
[16] Zou J,Omberg H,Trygve C.Prediction of TLP responses:model test vs.analysis[C]//Offshore Technology Conference Houston.Texas:[s.n.],2003:OTC 15348.
[17] WANG Li-zhong ,GUO Zhen,YUAN Feng.Quasi-static three-dimensional analysis of suction anchor mooring system[J].Ocean Engineering,2010,37:1127-1138.
[18] Ying MinLow,SaiHungCheung.On the long-term fatigue assessment of mooring and riser systems[J].Ocean Engineering,2012,53:60-71.
[19]元志明,嵇春艳,陈明璐.半潜式平台完全时域耦合运动分析[J].海洋技术,2010,29(4):81-87.(YUAN Zhi-ming,JI Chun-yan,CHEN Ming-lu.Full time domain coupled analysis of semi-submersible platform[J].Ocean Technology,2010,29(4):81-87.(in Chinese))
[20]杨敏冬,滕斌.海洋系泊缆索非线性有限元静力分析[J].海洋工程,2009,27(2):14-20.(YANG Min-dong,TENG Bin.Static analysis of mooring lines using nonlinear finite element method[J].The Ocean Engineering,2009,27(2):14-20.(in Chinese))
[21]陆鑫森.高等结构动力[M].上海:上海交通大学出版社,1992.(LU Xin-sen.Advanced Structural Dynamics[M].Shanghai:Shanghai Jiao Tong University Press,1992.(in Chinese))
[22]史琪琪,杨建民.半潜式平台运动及系泊系统特性研究[J].海洋工程,2010,28(4):1-8.(SHI Qi-qi,YANG Jina-min.Research on hydrodynamic characteristics of a semi-submersible platform and its mooring system[J].The Ocean Engineering,2010,28(4):1-8.(in Chinese))
