综合考虑泵的设备及运行费用的换热网络优化

吴敏，肖武，贺高红

（大连理工大学精细化工国家重点实验室，膜科学与技术研究开发中心，辽宁 大连 116024）

从20世纪60年代起，换热网络综合就作为过程设计的一个子问题而受到重视，具有重要的理论意义和实用价值。近四十年来，换热网络综合一直是一个十分活跃的领域，常用的解决换热网络综合方法有夹点法[1-3]和数学规划法[4-5]。

无论是夹点设计法还是数学规划法，对换热网络的压降问题都没有进行全面的考虑。Polley等[6]在其文章中提到过一个实例，某个换热网络改造项目通过安装 50 000英镑的换热面积，可节省每年250 000英镑的公用工程费用，但最后需要购买1 000 000英镑的泵来克服流动阻力。该实例说明了压降因素对换热网络的综合有重要的影响，在换热网络的综合和改造中，压降也是一个需要考虑的关键因素。Polley等[7]指出，不考虑压降会造成两种不合理的情况：第一，设计的压降值远高于允许值，须重新设计；第二，实际压降远小于允许值，这将会导致安装更多的换热面积，产生不合理的投资关系。

为了维持换热网络的稳态运行，需要克服流体在流经换热器时产生的压降，故换热网络设计中泵的安装必不可少。因此，换热网络的压降是换热网络设计中需要考虑的重要因素，故在换热网络设计中需将泵的设备购置费用及运行费用同换热设备面积、换热设备个数、公用工程费用同时进行考虑。以往的换热网络综合研究中通常将流股给热系数作为常数来处理，但由于流股给热系数与流速及换热器的几何尺寸有着密切关系，这将会导致换热网络设计结果偏离实际工况，甚至不能设计施工。因此，换热网络综合中不仅要协调换热设备投资费用、换热设备个数和公用工程费用三者之间的关系，还需要对流股给热系数和压降同时进行优化。

Polley等[7]首先提出了考虑压降的换热网络综合和换热器单体设备设计同时考虑的设计方法；Zhu和Nie等[8-9]基于夹点技术，考虑压降因素综合优化换热网络；Serna和Ponce等[10-11]基于Yee的分级超结构[5]和夹点法[1]，考虑了压降的影响；Soltani和 Shafiei等[12]在对换热网络进行改造的过程中考虑了压降的影响。本文基于文献[13]所提出的非等温混合有分流的分级换热网络超结构模型，考虑了压降所引起的新增泵设备费用以及运行泵的能耗费用，且去除流股给热系数为常数的假设，建立了考虑泵的设备及运行费用的换热网络同步综合的MINLP数学模型。采用改进的拟并行遗传/模拟退火算法同步优化换热设备费用、换热单元个数、公用工程费用以及流阻引起的额外费用，使得换热网络的优化设计更为可靠合理。

1 数学模型

在换热网络设计中，有些物流需要被加热，有些物流需要被冷却，如何将这些物流进行合理的匹配，使系统尽可能多的回收热量，减少冷、热公用工程的投入，使得整个网络年费用最小，并使每个过程物流达到规定的目标温度，这就是换热网络设计需要解决的问题[14]。

以两个热物流和两个冷物流为例说明分级超结构[5]模型，如图1所示。超结构级数为Nk=max{NH,NC}，每一级中匹配的次数为NH×NC，其中NH为热流股数目，NC为冷流股数目。图中冷、热公用工程设置在超结构的两端，Hi（i=0,1,2,··,NH）表示热流股，流向从左向右；Cj（j=0,1,2,··,NC）表示冷流股，流向从右向左。

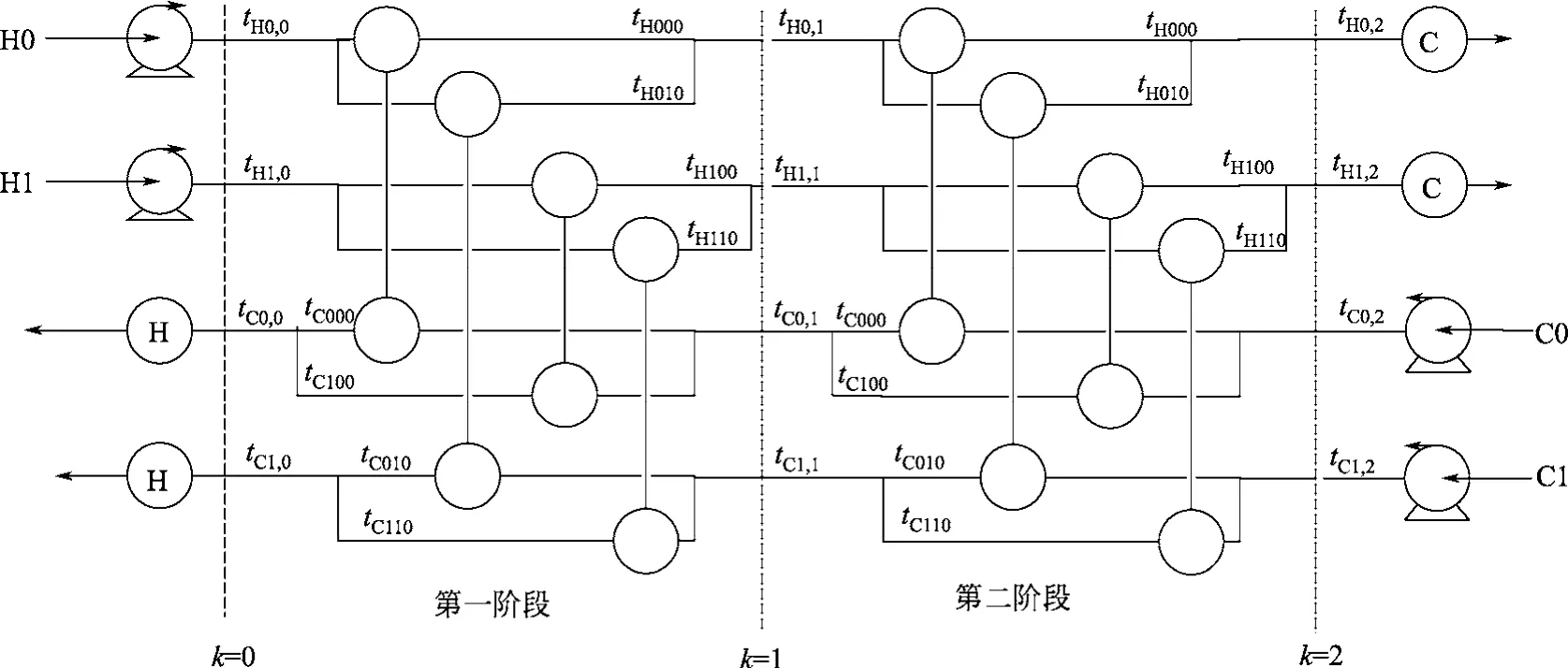
图1 考虑泵的超结构示意图

本文考虑了换热器压降所引起的新增费用，去除了流股给热系数为常数的假设，对非等温混合分级超结构模型进行改进，建立了更符合实际的换热网络同步综合的MINLP数学模型。

1.1 目标函数

以最小年度总费用作为目标函数，目标函数包括公用工程费用、设备投资费用、运行泵的能耗费用，其中设备费用包括换热器设备和泵的设备费用，如式（1）所示。

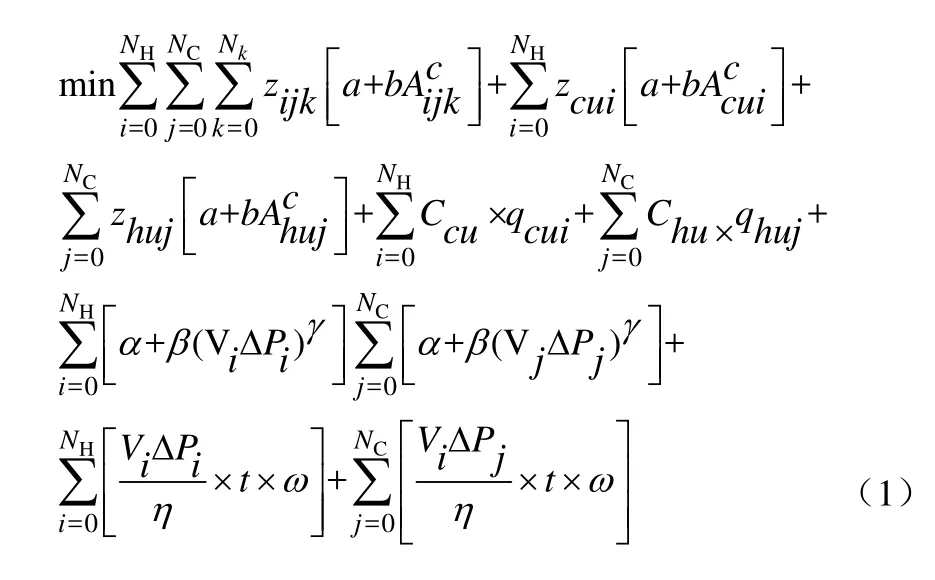
换热设备（换热器、加热器、冷却器）费用的计算公式为a+bAc，其中第一项a为换热设备固定费用，第二项为换热设备的面积费用，b、A、c分别为换热设备系数、换热面积、指数；公用工程费用的计算公式为C×q，其中C为公用工程单价，q为公用工程热负荷；泵的设备费用计算公式为α+β(VΔP)γ，其中第一项α为泵的固定费用，第二项为购买泵的费用，β、V、ΔP、γ分别为泵系数、泵所在流股的体积流量、该流股的压降、指数；运行泵的能耗费用的计算公式为t×ω×VΔP/η，其中t为年运行时间，ω为电的单价，V、ΔP、η分别为流股的体积流量、相应流股的压降、泵的运行效率。

1.2 约束条件

流股的热平衡约束、换热器的热平衡约束、流股的质量平衡约束、可行温度约束、温差约束、非负约束、离散变量等见文献[3]。在本文中，非等温混合的能量平衡约束、压降约束、流股流速的约束如下所述。

（1）非等温混合下第k级分流与混合的能量平衡

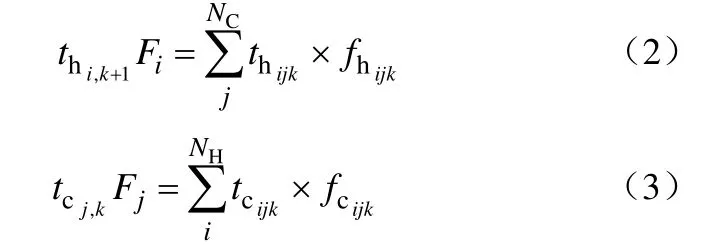
（2）压降约束

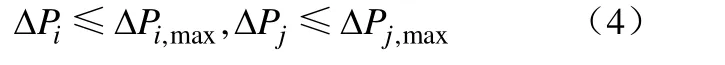
（3）换热器管/壳层流速约束

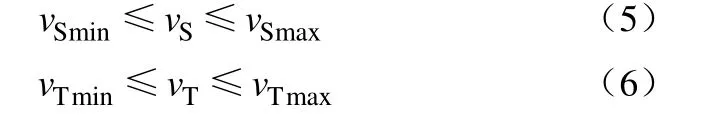
换热器压降的计算和给热系数的计算采用Frausto-Hernández等[15]使用的方法，流股的压降主要是与流股的给热系数、换热面积和换热器的结构相关，其计算见式（7）和式（9）。流股给热系数是流股流速的函数，其计算见式（8）和式（10）。流股流速作为遗传/模拟退火算法中的一个基因，其中流股的给热系数是关于流股流速的函数，而流股的压降是关于给热系数的函数。因此，流股的压降和给热系数都受到了流股流速的约束，两者都随着流速的变化而变化，故而换热网络的优化综合过程中需要确定一个最优的流股流速来达到全局最优的目的。

式中，下角标S和T分别为换热器的壳程和管程；KPT和KPS分别为与换热器几何形状以及流股物性相关的管程参数和壳程参数，其计算方法采用Serna等[16]提出的式（11）和式（12）。

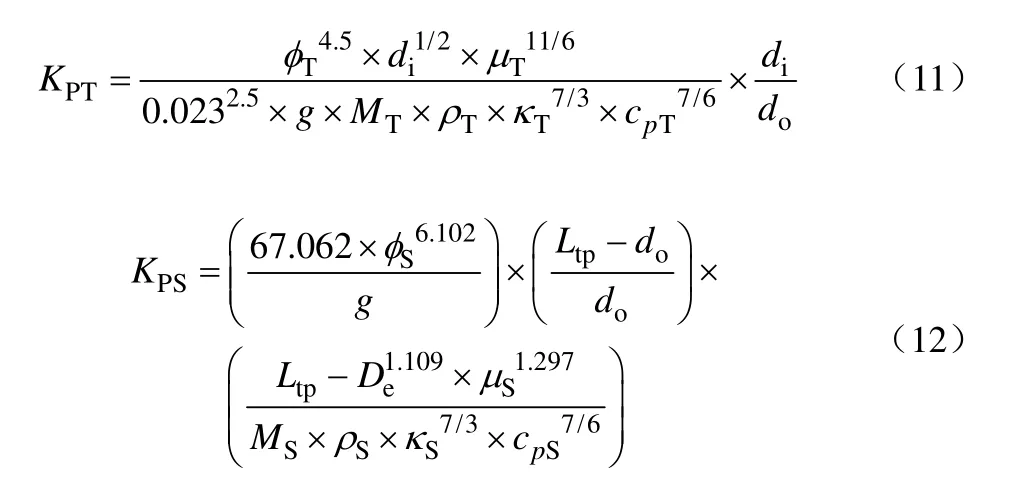
式中，φ为黏度修正因子，因为黏度和温度密切相关；μ为黏度；ρ为密度；g为重力常数；Ltp为换热器管间距；De为换热器管当量直径；κ为热导率；di为管内径；do为管外径；cp为比热容；M为流股质量流量。

在对换热器压降的计算过程中，需要考虑到换热设备并联和串联的情况。对于这种情况，Shenoy[17]曾提出过一种近似处理方法，认为换热设备的面积和该换热器的压降值成正比，故可根据换热器的面积大小将整条流股的压降值进行线性的分配。这种处理使得计算压降的过程中忽略了对并联和串联情况的考虑，避免了计算分级超结构中每一级的压降值，大大减小了数学模型的复杂性但会使综合出的换热网络偏离实际情况。对换热设备的串联和并联的情况处理方式如下所述。

换热设备串联见图2及式（13）。

换热设备并联见图3及式（14）。

在处理换热设备的并联结构时，本文采用了Zhu等[8]所提出的处理方法，将并联结构中压降最大的分支流股压降值作为该并联结构的压降。

2 GA/SA算法求解策略

以上换热网络优化综合模型是包含大量连续变量和离散0-1变量的MINLP模型，先确定换热器是否存在，然后确定每个换热器换热量的大小、流经换热器的冷/热流股的热容流率、换热器管/壳层流股的流速，进而计算出每个换热器的压降大小和每个换热器的面积，最后得出该换热网络结构下换热网络年费用。遗传算法[18]（genetic algorithms，GA）和模拟退火算法[19]（simulated annealing algorithms，SA）是目前解决全局优化比较有用的方法，这些算法都是模拟自然界的自然现象进行大规模优化问题的随机方法，两种算法都不要求目标函数的连续性、可微性及凸性，而且算法简单、易于实现。

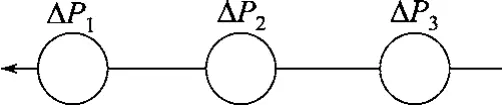
图2 换热器串联

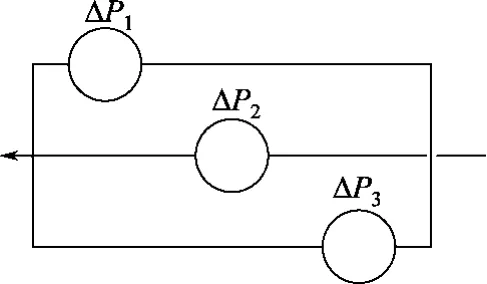
图3 换热器并联

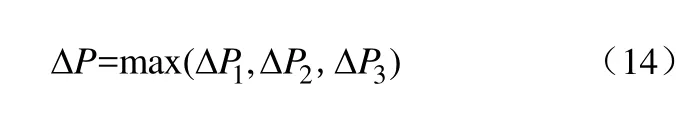
传统的遗传算法具有提前收敛的缺陷，模拟退火算法具有跳出局部最优解、向全局最优解所在区域靠近的特点。故将两种算法结合起来就可以兼顾局部和整体，容易得到全局最优解。遗传/模拟退火算法即将模拟退火算法嵌入到遗传算法中，在使用遗传算法之前首先对初始种群中的每个个体应用模拟退火算法，使最优个体替代原种群中的个体形成一个新种群，然后对新种群应用遗传算法。遗传/模拟退火算法有较强的鲁棒性，适合大规模的复杂系统求解，使获得最优解的能力增强。

求解步骤如下所述。

（1）设置算法参数，比如单个种群规模creanum、退火代数 annealgen，最大交叉系数max-cc、最小变异系数 maxmc1、最大变异系数maxmc2、无进展最大代数的 max_val、竞争系数pmax。

（2）运用C程序中的random函数初始化种群个体，构成初始种群，种群中的每个个体具有5个基因：热交换量q、热流股分支热容流率fh、冷流股分支热容流率fc、流股管程流速vT、流股壳程流速vS。

采用SPSS 18.0统计学软件对所得数据进行分析处理，计量资料用（±s）表示，采用 t检验，计数资料用[n（%）]表示，采用 χ2检验，P＜0.05 为差异有统计学意义。

（3）首先对初始种群中的每个个体应用模拟退火算法进行处理得到拟子种群。

（4）然后应用遗传算法对拟子种群进行交叉、变异处理。

（5）满足终止条件时终止。

3 实例求解

该算例首先由 Silva和 Zemp[20]提出，后来被Soltani等[12]引用，有2条热流股和3条冷流股，具体数据及物性参数列于表1。

该算例求解过程中，GA/SA算法中子种群数为4，种群个体规模为100，交叉、变异率给定初始值，而在进化的过程中取值随个体相似度变化而自适应确定。当种群中的最优个体在50代内不再进化，则输出最优解。采用GA/SA算法编程求解本算例，得到最优的换热网络结果列于表2，换热网络结构如图4所示。该超结构MINLP数学模型包括23个离散变量，95个连续变量。用C语言基于GA/SA算法编写程序，在Intel 2.10 GH，2G RAM的电脑上运行该程序，用时1CPU秒得出计算结果。

该算例使用如下的计算公式和经济数据：换热设备年度价格公式为30000+750A0.81$；热公用工程使用300 ℃的蒸汽，其价格为60 $/kW；冷却公用工程使用进口温度为15 ℃、出口温度为25 ℃的冷却水，其价格为 6 $/kW；泵购置价格为 2000+5（VΔP）0.68，泵的运行效率为70%；电的价格为0.05$/kW；设备年运行时间为8000 h。

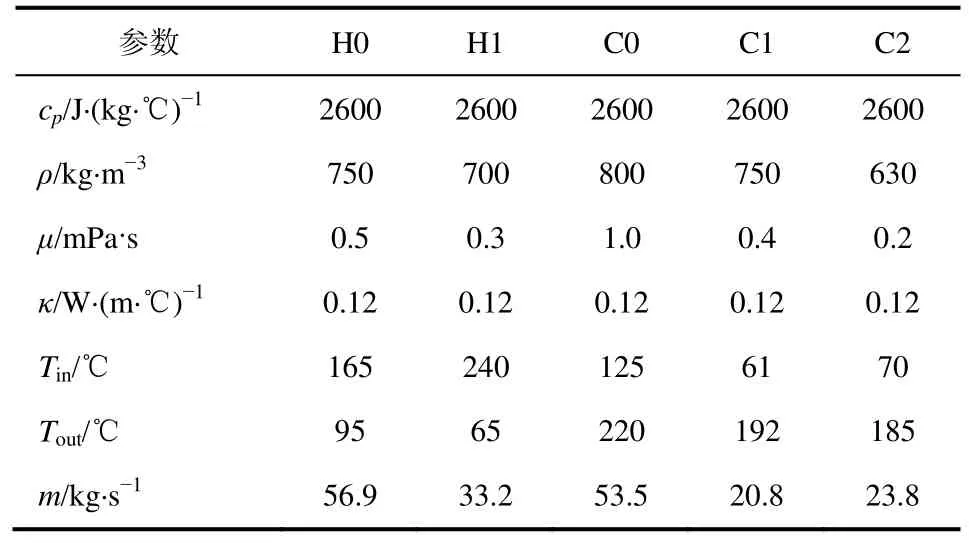
表1 物性参数

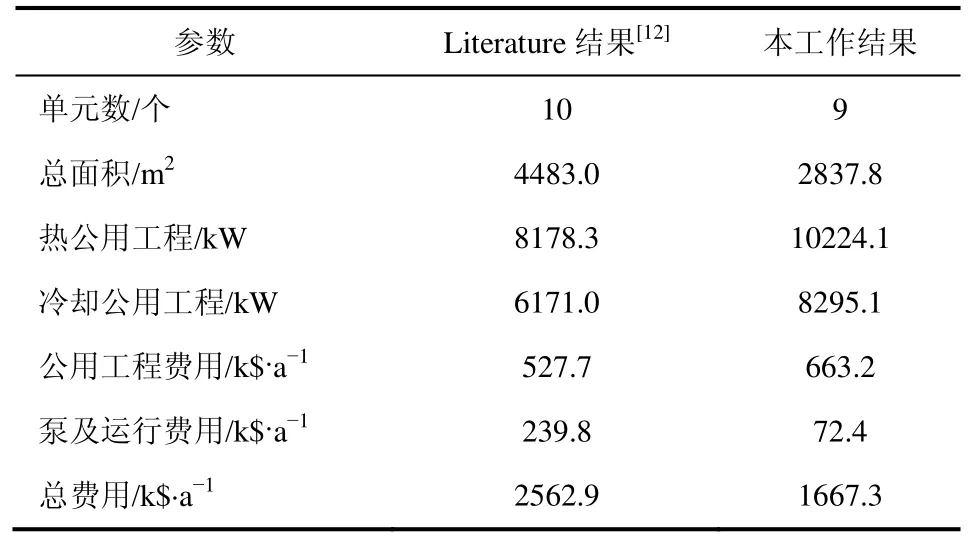
表2 换热网络设计结果比较

表2给出了优化的换热网络结果，表3给出了每个换热器最优的管/壳层给热系数。由表2和表3的计算结果，在对算例应用相同的经济数据的条件下，本文优化后的换热网络：传热设备个数为9个，比文献减少1个；传热单元总面积为2837.8 m2，比文献小1645.2 m2，即降低了36.7%；年公用工程费用为663.2 k$，比文献高135.5 k$，即升高了25.7%；泵的投资和运行费用为72.4 k$，比文献低167.4 k$，即降低了69.8%；换热网络年总费用为1667.3 k$，比文献小895.6 k$，即降低了34.9%。

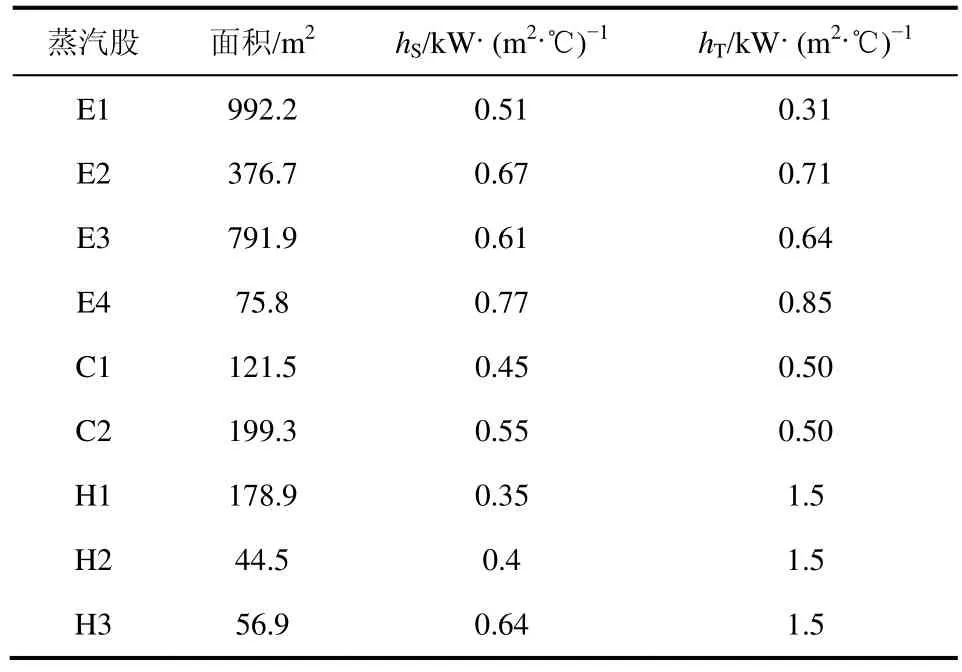
表3 换热设备的面积分配、给热系数

4 结 论

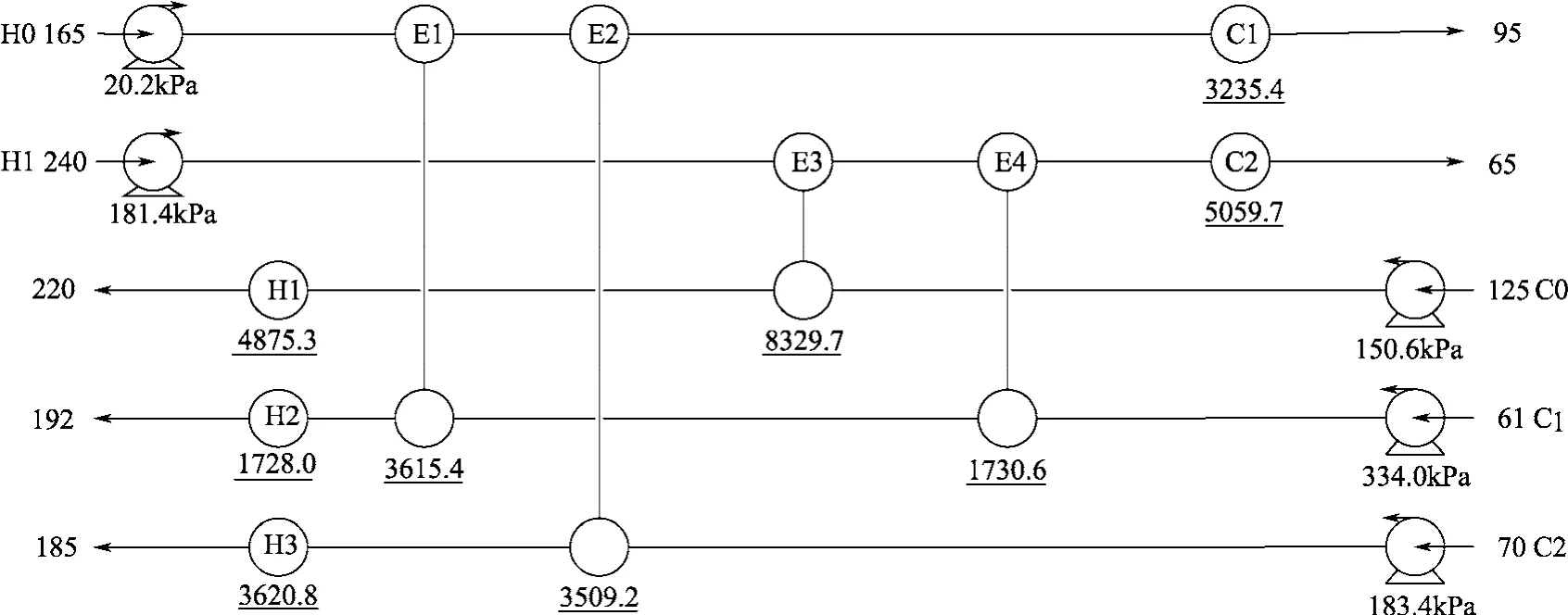
图4 换热网络优化结果

符 号 说 明

A——换热面积，m2

cu，hu——分别为冷、热公用工程

do，di——分别为换热器管的外径和内径，mm

F——热容流率，kW/℃

fc，fh——分别为冷、热分支流股的热容流率，kW/℃

hS，hT——分别为换热器壳程、管程给热系数，kW/(m2·℃)

i，j——分别为热流股和冷流股标号

k——分级超结构级数

LMDT——对数平均温度差，℃

q——换热器换热量，W

TCin——冷流股进口温度，℃

TCout——冷流股出口温度，℃

THin——热流股进口温度，℃

THout——热流股出口温度，℃

tcijk——冷分支流股某点温度，℃

tcj，k——换热网络冷干流股某点温度，℃

thijk——热分支流股某点温度，℃

thi，k——换热网络热干流股某点温度，℃

t——设备年运行时间，h

v——换热器中流体的流速，m/s

ω——电的单价，$/kW

Z——热面积存在情况，值为0或1

下角标

in，out——分别为物流入口、出口

S，T ——分别为换热器的管程、壳程

[1]Linnhoff B，Hindmarsh E.The pinch design method for heat exchanger networks[J].Chemical Engineering Science，1983，38（5）：745-763.

[2]Linnhoff B，Ahmad S.Cost optimum heat exchanger networks—1.Minimum energy and capital using simple models for capital cost[J].Computers and Chemical Engineering，1990，14（7）：729-750.

[3]Yee T F，Grossmann I E.Cost optimum heat exchanger networks—2.Targets and design for detailed capital cost models[J].Computers and Chemical Engineering，1990，14（7）：751-767.

[4]Papoulias S A，Grossmann I E.A structural optimization approach to process synthesis-Ⅱ.Heat recovery networks[J].Computers &Chemical Engineering，1983，7（6）：707-721.

[5]Yee T F，Grossmann I E.Simultaneous optimization models for heat integration - Ⅱ.Heat exchanger network synthesis[J].Computers and Chemical Engineering，1983，7（10）：707-721..

[6]Polley G T，Panjeh Shahi M H.Pressure drop considerations in the retrofit of heat exchanger networks[J].Transactions of Institute of Chemical Engineers，1990，68（3）：211-220.

[7]Polley G T，Panjeh Shahi M H.Interfacing heat exchanger network synthesis and detailed heat exchanger design[J].Transactions of Institute of Chemical Engineers，1991，69（A6）：445-457.

[8]Zhu X X，Nie X R.Pressure drop considerations for heat exchanger network grassroots design[J].Computer and Chemical Engineer，2002，26（12）：1661-1676.

[9]Zhu X X，Nie X R.Heat exchanger network retrofit considering pressure drop and heat-transfer enhancement[J].AIChE Journal，1999，45（6）：1239-1254.

[10]Serna-Gonzalez M，Ponce-Ortega J M.Two-level optimization algorithm for heat exchanger networks including pressure drop considerations[J].Industry & Engineering Chemistry Reserach，2004，43（21）：6766-6773.

[11]Serna-Gonzalez M，Ponce-Ortega J M.Total cost target for heat exchanger network considering simultaneously pumping power and area effects[J].Applied Thermal Engineering，2011，31（11-12）：1964-1975.

[12]Soltani H，Shafiei S.Heat exchanger networks retrofit with considering pressure drop by coupling genetic algorithm with LP（linear programming） and ILP （integer linear programming）methods[J].Energy，2011，36（5）：2381-2391.

[13]Wei Guanfeng，Sun Yaqin.Multi-stream heat exchanger networks synthesis with improved Genetic algorithm[J].Journal of Dalian University of Technology，2004，44（2）：218-223.

[14]姚平经.过程系统分析与综合[M].大连：大连理工大学出版社，1995.

[15]Frausto-Hernándeza S，Rico- V.MINLP synthesis of heat exchanger networks considering pressure drop effects[J].Computers &Chemical Engineering，2003，27（8-9）：1143-1152.

[16]Serna M，Jimenez A.A compact formulation of the Bell-Delaware method for heat exchanger design and optimization[J].Chemical Engineering Research and Design，2005，83（A5）：539-550.

[17]Shenoy U V.Heat exchanger network synthesis.Process optimization by energy and resource analysis[M].Houston：Gulf Publishing Company，1995.

[18]Dolan W B.Algorithmic efficiency of simulated annealing for heat exchanger network design[J].Computers and Chemical Engineering，1990，14（10）：1039-1050.

[19]Goldberg D.Genetic algorithms in search，optimization and machine learning[M].New York：Addision-Wesley，1989.

[20]Silva M，Zemp R J.Retrofit of pressure drop constrained heat exchanger network[J].Applied Thermal Engineering，2000，20（15-16）：1469-1480.