降雨在时间分布的多重分形特征及对泥石流预测的指示

王春山

(成都地质矿产研究所，中国成都 610081)

定量研究降雨的时空分布特征是泥石流发生时预测预报的基础.虽然泥石流的时空预测预报一直都是研究者的关注点，并且取得了丰富的研究成果［1-4］，但在泥石流的预测预报实践中其准确性仍然是一个亟待解决的问题，尤其是在时间的预测方面.这主要是由于降雨在时空的不均匀性和随机性造成的.如何才能在无序的降雨过程中总结出触发泥石流的规律呢?上世纪70年代中期由伯努瓦·B·曼德布罗特创立的分形理论［5］将为解决这一问题提供一条好的途径.分形理论的研究对象为自然界和社会活动中广泛存在的无序而具有自相似性的系统，分形理论借助相似性原理为人们提供了一种新方法.但在大多数的物理现象中一致分形的描述过于简单化，一些复杂的系统的行为主要取决于某个物理量的空间(时间)分布，它表现的自相似性特征也是局域性的，具有空间(时间)分布的特征，如本文要讨论的降雨.因此多重分形理论便孕育而生，它是多个单分形在空间上的缠结、镶嵌，是分形科学的重要发展.许多学者在近三十年间将多重分形在环境学［6-7］、经济学［8-9］、地震学［10］和岩石力学［11-13］等领域中进行了深入的研究和应用，并取得了重要的进展和丰硕的成果，但在泥石流预测预警中的应用还处于起步阶段.分析特定沟谷降雨活动的多重分形性质，可以为我们揭示泥石流系统孕育、生长、触发的动态演化特征.本文采用多重分形指数谱来描述泥石流发生前后降雨活动在时间分布的分形结构，探讨了泥石流多重分形的预测意义.

1 多重分形的理论及计算方法

1.1 分形和多重分形

如果第i个盒子包含有一个α类型奇异性，则［pi(l)］q≈lqα.

因为α类型奇异性是定义在具有分形维数f(α)的几何上，包含这类奇异性的盒子数目应当满足分项分部，及随 lf(α)而变化.定义 n(α，l)为尺寸 l的盒子内含 α 类型奇异性的密度，则n(α，l)dα =p(α)l－f(α)dα，其中ρ(α)dα为分割尺寸变化时分形子集变化的数目.由此便可通过积分计算出函数z(q，l)，z(q，l)=∑［每个含 α 类型奇异性盒子的概率］q= ∫ρ(α)dαl－f(α)lτ(q).

1.2 多重分形的计算方法

多重分形函数的计算方法有很多，如矩方法、直方图法、小波法、乘数法，以及二次维矩方法等，而矩方法是其中最常用的方法［14］.本研究采用矩方法进行计算，具体步骤如下:

(1)对不同尺度下的数据构建测度函数μ=pi(l)/∑pi(l)，其中pi为某一划分尺度下第i个划分区间内雨量的总和，∑pi(l)为评价之间段内总雨量;

(3)求解质量指数τ(q)，将z(ε)与ε在双对数坐标图上绘出映射图，图形斜率就是质量指数τ(q);

(4)计算Holder奇异指数α(q)=dτ(q)/dq;

(5)利用公式1计算分形谱f(α).

1.3 降雨资料的多重分形处理

为研究降雨的变化特征与多重分形维数演化特征的关系，将研究时间段内的降雨量按照自然时间单位进行划分，即7 d、1 d、12 h、6 h、3 h、1 h、30 min和10 min，然后对各尺度内的雨量分布特征进行多重分形维数计算.因此本文中某日的降雨多重分形值是指由当日之前7天(包括当日)内雨量值计算的多重分形值.

2 降雨时间分布的自相似性分析

谢和平在专著《分形-岩石力学导论》［12］中引出多重分形学时，利用了具有密度和质量的初始元重新构造了Cantor集，在质量守恒的情况下按照一定规则分割、压缩初始元，形成一个多重分形集.而某一时间段的降雨情况则与Cantor集的情形相似，按照不同的时间间隔对雨量进行划分，可得到雨量的多重分形集.图1为2013年7月12日的雨量多重分形集，由此可以看出在特定时间内的降雨量具有多重分形特征.

图1 7月12日降雨量的多重分形集Fig.1 Multi fractal set rainfall in 12th July

3 降雨多重分形演化及泥石流演化预测

3.1 研究区概况及泥石流灾害

研究区域热水沟位于四川省甘孜州海螺沟风景区的中上游，沟口处为二号营地及热水沟温泉游泳池.最高点为5 888 m，最低点为2 425 m，相对高差为3 463 m，主沟床平均纵比降为343.3‰.山坡坡度一般为30°～36°，最大达53°.洪水期一般为每年的6～9月.上游主要分布中细粒似斑状黑云母花岗岩，中下游主要分布二叠系及第四系地层，主要为下二叠统中段灰岩、白云岩、石英片岩，下二叠统上段大理岩夹云母石英片岩，上二叠统绿片岩、石英岩夹板岩、大理岩及冰川堆积.受磨西断裂带的影响，区内构造较为复杂.

7月12日23点30分至13日0点左右，泸定县磨西镇海螺沟风景区的3号营地发生了泥石流，该次泥石流规模较大，约12万m3，虽无人员伤亡，但造成了严重的损失.此次泥石流的发生主要是由连续的长时间降雨引起山体滑坡溃坝导致.由于在热水沟流域布置了监测设备，因此完整地记录了该次泥石流发生时以及之前半个月的雨量资料.从7月8日到7月12日23点40分累计降雨达173.3 mm，其中7月10日24小时降雨量为60.7 mm，7月11日为33 mm，7月12日截至泥石流发生时降雨为26.9 mm.

3.2 降雨的多重分形谱特征

对于降雨时间段的划分，不同学者有不同的划分方法［15-16］，为了使本次的研究与前人的成果具有对比性，作者借鉴已有的划分方法，利用多重分形的矩方法按照10 min、30 min、1 h、3 h、6 h、12 h和24 h这7个时间尺度对雨量数据进行计算.进而得出7天内热水沟降雨量的多重分形特征谱曲线.然后以7天内的降雨量作为初始元，由泥石流发生之日起向前推进便可得到泥石流发生前不同时间段内降雨的多重分形特征谱曲线.研究不同降雨情况的特征谱曲线，便可得到泥石流发生时的预测预警特征值.所以下文提到的某日降雨多重分形谱其实为该日和其前6日的降雨情况多重分形.

不同的q值表示不同的概率测度μi在分配函数z(ε)中所具有的比重.当q为正值时，q越大则概率测度μi较大的部分所占的权重越大，是描述密集区;当q为负值时，q的绝对值越大则概率测度μi较小的部分所占的权重越大，是描述稀疏区［12］.在监测预警中，最需要关注的是集中降雨过程(密集区)特征，而对未降雨阶段(稀疏区)则可忽略，所以应选择q＞0的部分.已有学者论证得到了多重分形奇异谱的判定准则，认为合理的奇异谱曲线应当和直线f(α)=α相切［16］，即q=1.为此本研究的q值取1～99的正整数，通过计算得到6月22日～7月12日各7天时间段内降雨的多重分形特征谱曲线(图2).

按照热水沟降雨分布图(图3)可将降雨分为分散降雨、小幅集中降雨、降雨停顿和临灾降雨4种情况.

(1)分散降雨:6月29日和6月30日前降雨量较为分散，且雨量较少，在多重分形谱曲线上显示有拖尾的特征.因此可以认为再出现此种类型的多重分形谱图形时将不会发生泥石流(图4).

(2)小幅集中降雨:7月1—3日和7月4—5日出现了小幅集中降雨，由多重分形谱可以看出，曲线发生明显的变化，已经没有拖尾的现象且曲线斜率变大(图5).

图2 数天雨量多重分形谱Fig.2 The curve with the fractal spectrums of rainfall of several days

图3 热水沟雨量曲线图(10 min)Fig.3 The rainfall curve of Hot-water gully(10 minutes)

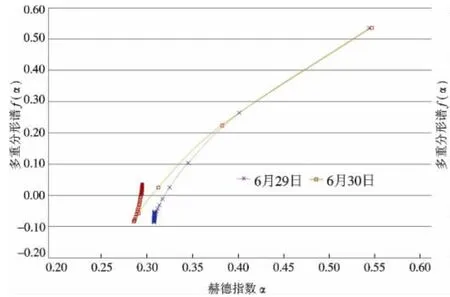
图4 分散降雨多重分形谱Fig.4 The curve of scattered rainfal

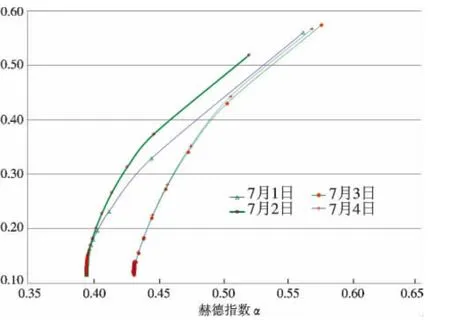
图5 小幅集中降雨多重分形谱Fig.5 The curve of small-scale rainfall

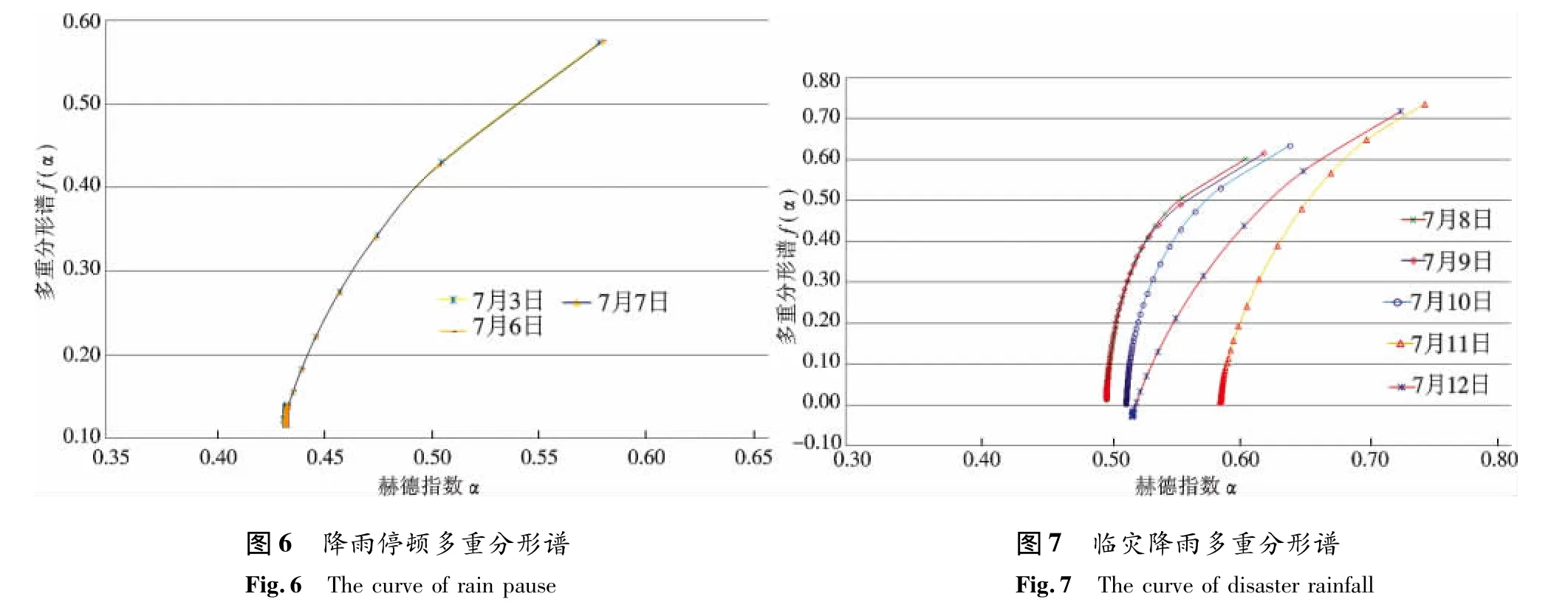
(3)降雨停顿:7月3日、7月6—7日为晴天，降雨量为零的情况，多重分形谱则近于重合.由此可以看出多重分形可以很好地表现降雨间歇时的情况(图6).

(4)临灾降雨:从7月8日下午4点开始，集中的降雨开始，期间并有短暂间歇.通过多重分形谱(图7)可以看出，7月8—11日，其降雨特点较为相似，而分形谱也表现出相似的趋势，只是随着降雨时间的持续，赫德指数α逐渐变大;7月12日晚10点的集中降雨导致泥石流的发生，此时多重分形谱较其他曲线更接近线性.

3.3 泥石流演化预测分析

有学者［17］采用多重分形谱f(α)中的3个参数(B、Δα和Δf)研究了大气污染物各年的多重分形谱的变化.其中Δα反映了标度不变的情况下，整个分形结构上概率测度分布不均匀性的程度和过程的复杂性，刻画了数据集的波动幅度，Δα越大，归一化指数概率测度分布越不均匀，数据波动越剧烈，对于降雨而言则表示降雨过程越强烈.Δf体现了标度不变的情况下，归一化指标处于波峰、波谷位置数目的比例，Δf＜0表示归一化指数更多地处于波谷，即晴天情况;Δf＞0，表示归一化指数更多地处于波峰，即降雨阶段，Δf越大则归一化指数越接近波峰.B反映曲线的不对称程度，由于本次研究的为曲线的一部分，不涉及曲线的对称性.所以本次采用Δα和Δf来进行多重分形谱的分析.本文中Δα和Δf为选取q为1和90两个数值时α和f(α)的差值.

将6月29日至7月12日降雨过程得到的多重分形进行计算得到Δα和Δf(表1).由表1可知，随着降雨强度波动幅度加大，Δα有逐渐变大的趋势，前期的Δα的数值较大是因为早期有较为强烈的降雨过程，为此还需要参考Δf值.由Δf的变化可以看出随着降雨强度的不断加大，Δf值也在逐渐升高，中间受到几个晴天的影响而略有起伏，直到泥石流爆发时Δf值突然猛增到0.8.由此可认为热水沟在Δα大于0.2，Δf接近0.8时将会发生泥石流灾害.

为了阐述的需要，文中的各条奇异谱曲线的时间间隔为24 h，在实际的预测预报中可以根据需要将该间隔缩短到1 h，甚至为10 min，进而达到实时预测的目的.

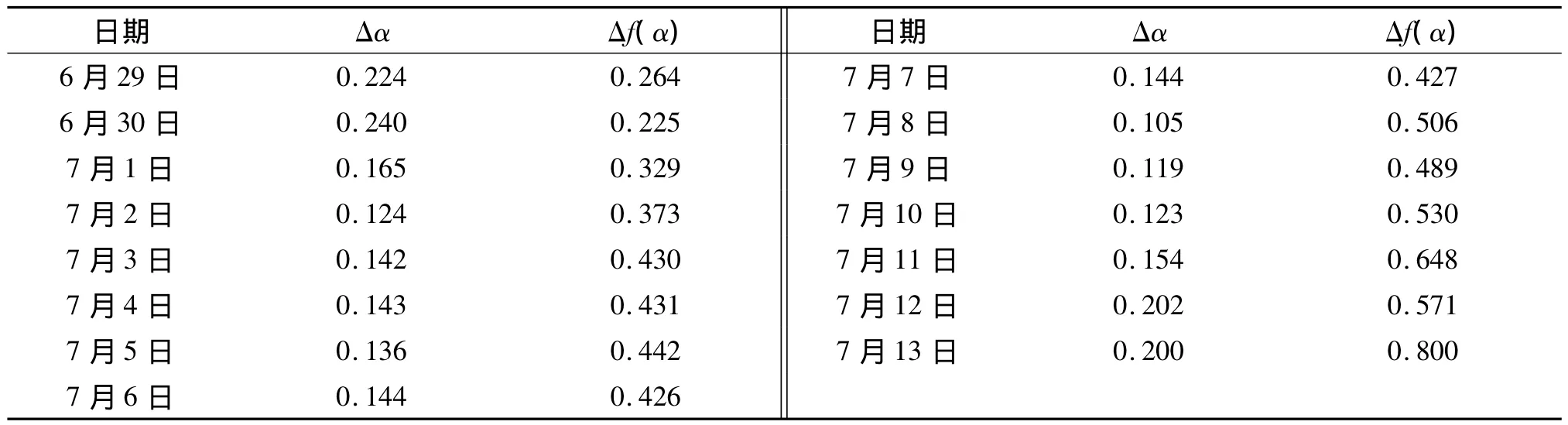
表1 Δα和Δf值统计表Tab.1 Statistical table of Δα and Δf

4 结论

本文利用多重分形理论对四川省甘孜州海螺沟风景区中热水沟7.12泥石流发生前近半个月的雨量资料进行了整理计算，得到以下结论:

(1)降雨过程在有限的尺度内具有自相似的特征，可以利用多重分形理论进行研究和分析;

(2)不同的降雨过程会呈现不同的多重分形谱，其Δα和Δf值也将随之发生变化，具有很好的规律性，仅对热水沟而言，当Δα大于0.2，Δf接近0.8时将会发生泥石流灾害;

(3)利用雨量进行泥石流预测预报应立足于详细地质调查的基础上，不同地区的泥石流发生时的多重分形特征将有所不同.

［1］白利平，南 赟，孙佳丽.北京市泥石流灾害临界雨量研究［J］.中国地质灾害与防治学报，2007，18(2):34-36.

［2］孟凡奇，李广杰，王庆兵，等.基于功效系数法的泥石流灾害预警研究［J］.岩土力学，2012，33(3):835-840.

［3］刘希林，燕丽萍，尚志海.基于区域临界雨量的广东省泥石流灾害易发区预测［J］.水土保持学报，2009，23(6):71-74.

［4］朱佳敏，姚素香，顾小丽.浙江宁波市地质灾害的雨量阈值及预报分析［J］.中国地质灾害与防治学报，2011，22(4):85-87.

［5］伯努瓦·B·曼德布罗特.大自然的分形几何学［M］.上海:上海远东出版社，1997.

［6］柯贤忠，程绪江，谢淑云，等.基于多重分形的表层土壤中重金属元素来源分析——以海南省琼海市为例［J］.地质科技情报，2010，29(1):97-102.

［7］史 凯，刘春琼，艾南山.上海市空气质量变化的多重分形分析［J］.环境污染与防治，2008，30(8):61-64.

［8］何建敏，常 松.中国股票市场多重分形游走及其预测［J］.中国管理科学，2002，10(3):11-17.

［9］崔美兰，李汉东.中国和国际汇率市场的多重分形比较［J］.北京师范大学学报:自然科学版，2011，47(5):546-550.

［10］唐礼忠，XIA K W，李夕兵.矿山地震活动多重分形特性与地震活动性预测［J］.岩石力学与工程学报，2010，29(9):1818-1824.

［11］刘树新，刘长武，韩小刚，等.基于损伤多重分形特征的岩石强度Weibull参数研究［J］.岩土工程学报，2011，33(11):1786-1791.

［12］谢和平.分形-岩石学导论［M］.北京:科学出版社，1996.

［13］王 敏，万 文，赵延林.基于MATLAB的岩体结构面曲线模拟及其分形研究［J］.湖南科技大学学报:自然科学版，2013，28(2):12-15.

［14］周广柱，王翠珍，刘意章，等.多重分形理论在环境科学领域的研究进展［J］.矿物岩石地球化学通报，2012，31(6):650-656.

［15］白利平，孙佳丽，南 赟.北京地区泥石流灾害临界雨量阈值分析［J］.地质通报，2008，27(5):674-680.

［16］胡桂胜，陈宁生，杨成林.成都市灾害性山洪泥石流临界降雨量特征［J］.重庆交通大学学报:自然科学版，2011，30(1):95-101.

［17］史 凯，刘春琼，艾南山.上海市空气质量变化的多重分形分析［J］.环境污染与防治，2008，30(9):60-64.