功率谱熵在垂直于水平流向的气液两相流压差信号中的应用

董芳，方立德，李小亭

（河北大学质量技术监督学院，河北保定 071002）

功率谱熵在垂直于水平流向的气液两相流压差信号中的应用

董芳，方立德，李小亭

（河北大学质量技术监督学院，河北保定 071002）

对垂直于水平流向的气液两相流压差信号进行了实际测量，对采集的信号提取其功率谱熵值.结果表明：压差信号的功率谱熵受外界压力变化影响较小，对两相流流型变化是敏感的，通过分析功率谱熵值随气液两相流气相流速变化趋势，能够较好地揭示水平管道气液两相流流动特性，为两相流流型的准确识别方法提供有价值的参考.

气液两相流；压差信号；功率谱熵；流型

气液两相流动存在于众多工程领域中，例如石油、化工、动力、制冷、冶金等工业中的管道传输和化学过程中，准确地检测出两相流流动参数对于系统的计量、控制、节能、环保和运行可靠性等具有重要意义.在两相流量、管道形状、管道方向等因素的影响下，两相分界面的形状不断改变，无规律可循，并且相间存在相对速度，相对速度不同也会引起流动性质和流动结果发生很大变化，这些固有性质使得多相流问题的复杂性要远远高于单相流问题.

气液两相流的压差波动信号容易准确测量，并且携带大量关于流动分布的信息，因此，近年来很多学者针对气液两相流压差信号动力学特征进行研究［18］，分别利用混沌分形理论、多尺度信息熵理论、符号序列统计分析、递归定量分析等多种先进信息分析方法，对采集的压差波动信号进行分析处理，探求气液两相流动特性，以上研究均取得了良好的效果，为气液两相流流型识别方法研究提供了参考.然而，这些研究中的压差信号都是提取的沿着流动方向的两点之间的压差信号，即水平管道在水平方向取压，垂直管道在竖直方向取压.这种取压方法测取的压差信号会受到沿程摩擦阻力的影响，导致在不同的实验参数下不能得到统一的结论.文中针对水平管道在垂直于流动方向上提取压差波动信号，此压差信号与两相流流动的方向垂直，因此不会受沿程摩擦阻力的影响，对其进行分析处理可以很方便地进行流型识别.

功率谱熵分析作为一种非线性信息处理方法，具有计算过程简便、物理概念清晰等优点，已经较好地应用于一些复杂的非线性系统中［916］.在水平管道中对竖直方向的气液两相流压差信号进行了测量，为了探讨功率谱熵与气液两相流流动特性之间关系，从实际测量的96组压差信号中提取了功率谱熵，研究表明此功率谱熵值与水平管道气液两相流流型变化密切相关，并且受外界压力影响较小，是诊断与识别气液两相流流型的有效辅助工具.

1 实验装置及两相流压差波动信号采集

水平管气液两相流压差信号是在天津大学可调压中压湿气测量装置上进行两相流动态实验采集得到，此装置压力可调，实验连接实物图如图1所示.

图1 实验连接实物Fig.1 Physical map of the experimental facilities

实验中测量管段为方管，水平管段竖直方向的压差信号采用新型分体式高频压差变送器测量得到，该压差变送器分高压端、低压端2个探头，将2个探头直接与取压孔连接，避免了传统的压差测量中引压管造成的测量误差.此次实验主要模拟气相为主的气液两相流动，包括分层流、环状流、波状分层流，这3种流型特点是气相体积流量比液相大很多，气相的流速都高于液相.

实验温度为16～21℃，选择0.05MPa和0.1MPa 2个背景压力点，每个压力点下设置6个液相流量点（0.05，0.15，0.25，0.35，0.45，0.55m3／h），每个液相流量点下又分别设置8个气相流量点（20，40，60，80，90，120，150，180m3／h）.实验时，按照所设定的流动工况逐一调整水流量和气流量，流量稳定时等待5min之后再进行数据的记录.采样频率为1kHz，采样时间为15s，共采集96组压差信号.

2 功率谱熵

2.1 功率谱熵的定义

Kapur等［17］指出：对于一个不确定性系统，若其状态特征可以用一个随机变量X来表示，X的取值为

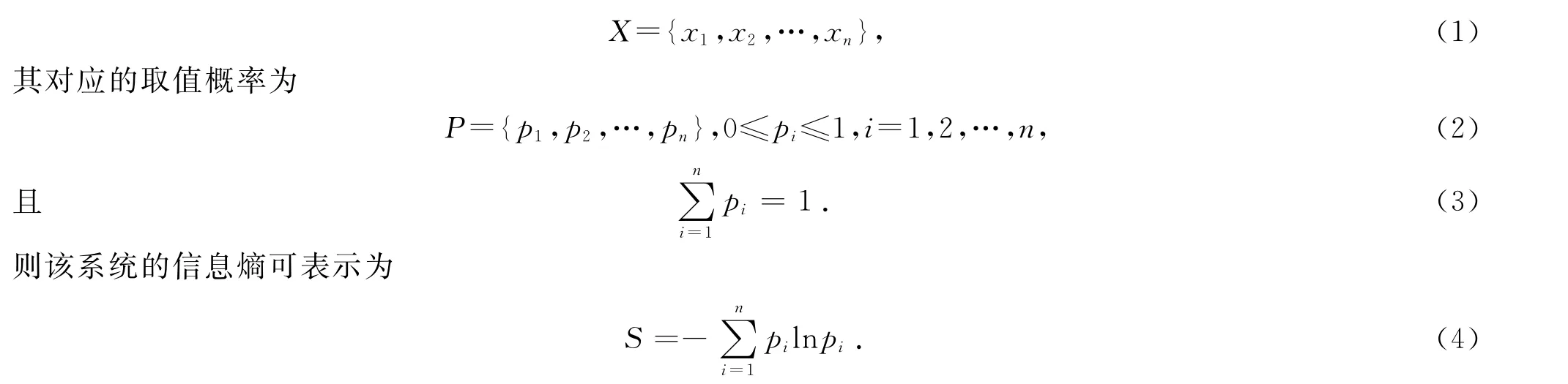
变量的不确定性越大，熵就越大.一个系统越是有序，信息熵就越低；反之，一个系统越是混乱，信息熵就越高.因此，信息熵可以作为系统有序化程度的一个度量.

Rezek等人［18］通过信息熵来定量计算不确定系统的功率谱的复杂性.采用FFT变换将时域信号转换为频域信号，然后估计序列的功率谱.

设长度为N的序列x（n）的DFT变换为x（f），则其功率谱密度的估计为

（8）式中pi表示第i个功率谱在整个频谱中占的百分比.

功率谱熵是从频域角度定义的信息熵，可作为系统在频域内的复杂程度的一种度量.构成某时间序列信号的过程数目越多，序列越复杂，则不确定度（功率谱熵）越大，反之若过程数目越少，序列越简单，则不确定度（功率谱熵）越小.

2.2 功率谱熵对一些常规信号的识别

为了进一步考察功率谱熵对不同复杂程度信号的辨别能力，对一些典型的时间序列选取4 096点计算功率谱熵，结果如表1所示.其中正弦周期信号的采样间隔为π／32，混合信号为正弦信号与高斯白噪声信号的混合序列，p为高斯白噪声信号的混入比例.

表1 不同类型信号的功率谱熵计算结果Tab.1 Results of spectral entropy for different type signals

从表1可以看出，从正弦信号到混合信号到高斯白噪声，功率谱熵的值呈增大的趋势，对于混合信号，其功率谱熵值随着其白噪声混入比例的增加而增大，介于正弦信号和高斯白噪声之间.综上所述，功率谱熵认为周期正弦信号不确定性最小，复杂性最低；高斯白噪声信号不确定性最大，复杂性最高；并且对不同随机程度的信号也能有效地区分，能对时间序列的复杂性程度进行有效地描述.

两相流是一个复杂的非线性动力学系统，利用功率谱熵作为气液两相流压差波动信号的复杂性度量，揭示两相流流动特性以及流型演变的规律.

3 功率谱熵在气液两相流压差波动信号中的应用

对采集的96组气液两相流差压波动信号进行处理，其中每个压力点下设置6个液相流量点，每个液相流量点下又分别设置8个气相流量点.为了减小序列长度对功率谱熵计算影响，对每种工况信号分别选取4 096个测量数据点计算其功率谱熵，结果如图2和图3所示.

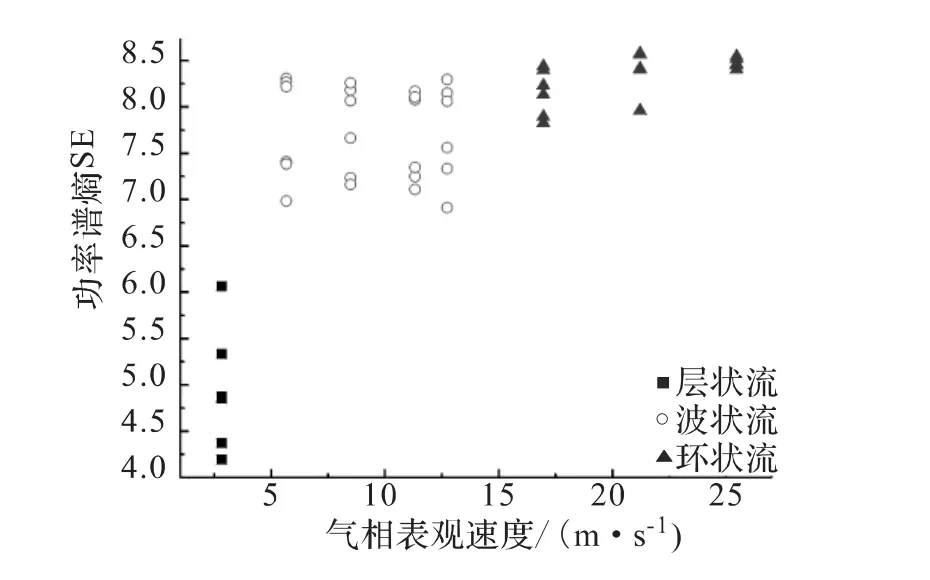
图2 在0.05MPa压力点下，SE与气相表观速度关系Fig.2 Diagram of spectral entropy and gas superficial velocity under the pressure of 0.05MPa

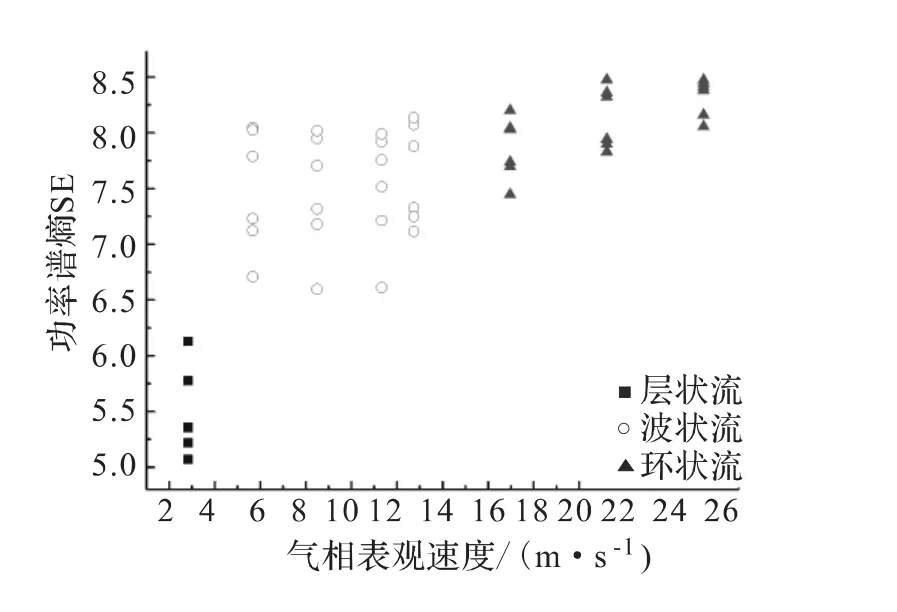
图3 在0.1MPa压力点下，SE与气相表观速度关系Fig.3 Diagram of spectral entropy and gas superficial velocity under the pressure of 0.1MPa

从图2图3可以看出，在2个压力点下，功率谱熵随气相表观速度变化趋势基本一致，表明用功率谱熵分析两相流流动特性受外界压力影响很小.总的变化趋势为随着气相表观速度的增加，功率谱熵值逐渐增加，说明差压波动信号不确定性逐渐增大，气液两相流动力学特性越来越复杂.

当气相表观速度小于5m／s时，水平管内呈现为典型的分层流流型，由于重力作用，气相分布在管道上部，液相分布在管道下部，气液两相之间存在较稳定的分界面，流动过程比较稳定，功率谱熵相比其他2种流型来说是最小的，并且在同一气相流速下，当液相流速不同时功率谱熵值差异较大.随着气相流速逐渐增加，当气相表观速度大于5m／s时，两相间稳定的分界面在气流带动下，沿流动方向出现连续波动，呈波浪状，气相流速越大，波动越剧烈，此时分层流转变为波状流，其动力学特性较分层流复杂，因此其功率谱熵值高于分层流.在同一气相流速下，当液相流速不同时功率谱熵值差异也较大，这一特点和分层流相似，说明分层流和波状流压差波动信号变化受液相流速影响较大.气相表观速度继续增加，当气相表观速度大于15m／s之后，气液分界面出现更为剧烈的波动，波峰甚至达到管道的顶部，气相将管顶部的液相波峰击碎，气相变为连续相，被击碎的液相在管顶部形成液膜，在气相带动下沿轴向缓慢流动，同时由于重力的存在，部分液体还向下流动，使得整个管道的圆周方向逐渐被液膜覆盖，环状流形成.在液相的重力和气相较高的表观流速的共同作用下，环状流的气液两相分界面出现毫无规律的随机波动，功率谱熵达到最大.但环状流型下，气相流速不变时，随液相流速变化压差信号的功率谱熵变化较小，说明环状流压差波动信号变化受液相流速的影响较小.

综上所述，功率谱熵对气液两相流流型变化是敏感的，不同流型下功率谱熵值有较明显的差异.通过分析功率谱熵值随两相流气相表观速度的变化规律，可以更深刻地揭示动力学系统内在特性，能够更好地反映水平管道典型流型转换规律，是理解气液两相流流型现象的有效指示器.

4 结论

1）将功率谱熵应用于水平管气液两相流竖直方向的压差波动信号中，计算过程简便，物理意义明确，并且受外界压力影响较小，为分析气液两相流流型转换特性提供了一种有效的新方法.

2）功率谱熵作为一种复杂性度量对气液两相流流型变化比较敏感，通过分析功率谱熵随两相流气相表观速度变化规律，表明此复杂性度量可以作为理解两相流流型现象的有效工具，为实现两相流流型的准确识别提供有价值的参考.

［1］ 丁浩，黄志饶，李海清.基于高阶谱的气液两相流差压波动信号的分析［J］.浙江大学学报：工学版，2006，40（1）：1-4.

DING Hao，HUANG Zhirao，LI Haiqing.Analysis of differential pressure fluctuation signal of gas-liquid two-phase flow based on higher-order spectrum［J］.Journal of Zhejiang University：Engineering Science，2006，40（1）：1 -4.

［2］ 孙斌，王强，周云龙.基于多尺度信息熵特征和RBF神经网络的气液两相流流型识别方法［J］.仪器仪表学报，2006，27（7）：725 729.

SUN Bin，WANG Qiang，ZHOU Yunlong.Identification method of gas-liquid two-phase flow regime based on multi-scale information entropy feature and RBF neural network［J］.Chinese Journal of Scientific Instrument，2006，27（7）：725-729.

［3］ 孙斌，周云龙，向新星，等.基于经验模式分解和概率神经网络的气液两相流识别 ［J］.中国电机工程学报，2007，27（17）：72-77.

SUN Bin，ZHOU Yunlong，XIANG Xinxing，et al.Identification method of gas-liquid two-phase flow regime based on empirical mode decomposition and probabilistic neural network［J］.Proceeding of the CSEE，2007，27（17）：72 -77.

［4］ 金宁德，苗龄予，李伟波.气液两相流差压测量波动信号的符号序列统计分析［J］.化工学报，2007，58（2）：327-334.

JIN Ningde，MIAO Lingyu，LI Weibo.Symbolic sequence statistical analysis of differential pressure measurement fluctuating signal of gas／liquid two-phase flow［J］.Journal of Chemical Industry and Engineering，2007，58（2）：327 -334.

［5］ 孙斌，周云龙，钟金山.基于复杂度特征的气液二相流流型识别方法［J］.化学工程，2008，36（4）：27-30.

SUN Bin，ZHOU Yunlong，ZHONG Jinshan.Identification method of gas-liquid two-phase flow regime based on complexity feature［J］.Chemical Engineering，2008，36（4）：27 -30.

［6］ 孙斌，李超，周云龙.基于递归定量特征的气-液两相流流型融合识别［J］.核动力工程，2009，30（6）：57-62.

SUN Bin，LI Chao，ZHOU Yunlong.Fusion identification method for gas-liquid two-phase flow regime based on recurrence quantification characteristics［J］.Nuclear Power Engineering，2009，30（6）：57-62.

［7］ 高娜，郑金吾，耿艳峰.槽式孔板差压信号的高阶统计量特征［J］.中国计量学院学报，2009，20（3）：214-218.

GAO Na，ZHENG Jinwu，GENG Yanfeng.Characteristics of the differential pressure signals of slotted orifice based on higher-order statistics［J］.Journal of China University of Metrology，2009，20（3）：214-218.

［8］ 孙斌，王二鹏，郑永军.气液两相流波动信号的时频谱分析研究［J］.物理学报，2011，60（1）：014701 -1 -014701 8.

SUN Bin，WANG Erpeng，ZHENG Yongjun.Time-frequency spectral analysis of gas-liquid two-phase flow＇s fluctuations［J］.Acta Physica Sinica，2011，60（1）：014701 -1 -014701 8.

［9］ 张佃中，谭小红，刘昭前.不同频段功率谱熵及其在心电分析中的应用［J］.湖南大学学报：自然科学版，2007，27（2）：75-79.

ZHANG Dianzhong，TAN Xiaohong，LIU Zhaoqian.Power spectral entropy of various frequency segments and its application to analysis electrocardiogram［J］.Journal of Hunan University：Natural Sciences，2007，27（2）：75-79.

［10］ PAPO DAVID，CAVERNI JEAN-PAUL，DOUIRI ABDEL，et al.Time-varying spectral entropy differentiates between positive and negative feed back-related EEG activity in a hypothesis testing paradigm［J］.International Journal of PsychoPhysiology，2007，66（3）：183-195.

［11］ 江波，王任一，齐红霞.混沌功率谱熵方法在识别水淹低阻油层中的应用［J］.江苏地质，2007，31（3）：232 -235.

JIANG Bo，WANG Renyi，QI Hongxia.Study on spectral entropy power identification method in water-flooded low re-sistivity zone［J］.Jiangsu Geology，2007，31（3）：232 -235.

［12］ MARTORANO P，FACCO E，FALZETTI G，et al.Spectral entropy assessment with auditory evoked potential in neuroanesthesia［J］.Clinical Neurophysiology，2007，118（3）：505-512.

［13］ 常洁，张佃中.心肌梗塞患者心电图（ECG）功率谱熵分析［J］.中国医学物理学杂志，2008，25（4）：768 770.

CHANG Jie，ZHANG Dianzhong.Power Spectrum Entropy（PSE）analysis of ECG signals of the myocardial infarction［J］.Chinese Journal of Medical Physics，2008，25（4）：768-770.

［14］ 任亚莉.基于功率谱熵和频带能量的运动意识任务分类研究［J］.计算机应用与软件，2010，27（12）：105 107.

REN Yali.On power spectral entropy and frequency band energy-based classification of movement consciousness task［J］.Computer Applications and Software，2010，27（12）：105-107.

［15］ 黄献，宋治，郑文，等.功率谱熵在痫性发作大鼠脑电检测中的应用研究［J］.中国应用生理学杂志，2010，26（2）：170-171.

HUANG Xian，SONG Zhi，ZHEN Wen，et al.Study about power spectral entropy and its application in EEG in epileptic rats［J］.Chinese Journal of Applied Physiology，2010，26（2）：170-171.

［16］ MORGAZ J，GRANADOS M M，DOMINGUEZ J M，et al.Evaluation of spectral entropy to measure anaesthetic depth and antinociception in sevoflurane-anaesthetised Beagle dogs［J］.The Veterinary Journal，2011，188（3）：352 -355.

［17］ KAPUR J N，KESAVAN H K.Entropy optimization principles with applications［M］.Boston：Academic Press，1992：35 -36.

［18］ REZEK I A，ROBERTS S J.Stochastic complexity measures for physiological signal Analysis［J］.IEEE Transactions on Biomedical Engineering，1998，45（9）：1186-1191.

（责任编辑：孟素兰）

Application of spectral entropy on the differential pressure signals against to the horizontal flow direction in gas-liquid two-phase flow

DONG Fang，FANG Lide，LI Xiaoting
（College of Quality and Technical Supervision，Hebei University，Baoding 071002，China）

The differential pressure fluctuation signals against to the horizontal flow direction were measured in gas-liquid two-phase flow，and then the spectral entropy was extracted from these signals.The results indicated that the spectral entropy was less affected by ambient pressure and sensitive to the flow pattern.By analyzing the rules of spectral entropy with the changes of gas phase velocity，the movement characteristic of gas-liquid two-phase flow was revealed deeply.It could serve as valuable references for precise identification of flow pattern.

gas-liquid two-phase flow；differential pressure signals；spectral entropy；flow pattern

董芳（1980-），女，河北青县人，河北大学讲师，主要从事多相流检测技术方向研究.Email：dongfang1023＠163.com

TP29

A

1000 -1565（2014）05 -0541 06

10.3969／j.issn.1000 -1565.2014.05.017

2014-03 -12

国家自然科学专项基金资助项目（61340028）；河北省高等学校科学技术研究指导项目（Z2013123）；河北大学自然科学研究计划项目（2010Q14）