基于改进SIR模型的甲型H1N1流感防控研究

孙 海， 熊思灿， 吴志强

(1.乐山师范学院数学与信息科学学院，四川乐山 614000;2.东华理工大学理学院，江西抚州 344000)

甲型H1N1流感是一种由A型甲流感病毒引起的猪呼吸系统疾病，该病毒可在猪群中造成流感的爆发。目前，此种病毒已在人群中大量爆发，它的潜伏期较流感、禽流感潜伏期长，病毒可能在人体潜伏7天后才表现出病症，感染后一般会在一周或一周多后就发病。所以分析感染人群的变化规律具有十分重要的意义。

霍阔等(2010)采用四阶Runge-kutta方法，利用一般SIR模型(姜启源等，2003;刘来福等，1997;李伟等，2004;李建奎等，2004;宇永仁等，2005;王汝发等，2004;周永卫等，2007)对甲型 H1N1流感传播进行了研究，本文在此模型的基础上进行了改进，增加了人群种类:潜伏者和接种疫苗者，且对他们间的转化系数也做了相应的改变，增加了每日潜伏者中转化为病毒携带者的比例和易感染者的接种疫苗比例，这样就使得模型更接近实际情况。

1 改进SIR模型的建立和求解

1.1 模型的假设与符号的约定

1.1.1 模型假设

(1)假设人群总数不变，并且不考虑这段时间内的人口出生率和自然死亡率及因其他疾病死亡和国内人口流动情况;

(2)假设以天作为时间计量单位;

(3)假设甲型H1N1流感潜伏期为7 d，在发病前1 d就具有传染性;

(4)假设由于一旦发现流感，就会加强防控，而且防控措施到位，凡感染者均能去医院就医，并成为确诊者;

(5)假设治愈恢复者对甲型H1N1病毒有免疫力，不再感染;

(6)假设甲型H1N1流感的死亡率为0;

(7)假设所有的统计数据真实，没有遗漏现象。

1.1.2 符号约定

S(t)为t时刻易感染者在人群中所占的比例;I(t)为t时刻感染者在人群中所占的比例;R(t)为截止到t时刻累计治愈恢复者在人群中所占的比例;V(t)为截止到t时刻累计接种疫苗者在人群中所占的比例;L(t)为潜伏者在人群中所占的比例;r为每天已确认成为治愈者的比例;p为每个携带甲流病毒者的日平均传染率;q为每日潜伏者中转化为病毒携带者的比例;l为每日潜伏者发病成为感染者的比例;v为易感染者的接种疫苗比例。

1.2 模型的建立

由以上假设和符号的约定，可以得到改进的SIR模型甲型H1N1流感各类人群间的关系转化如图1所示:

图1 改进的SIR模型的各类人群间的关系图Fig.1 Relationship graph of all kinds of people based on the improved SIR model

由图1可以看出，不同人群间增加了更多的转换过程:易感染者可以向潜伏者或接种疫苗者转化;潜伏者可以向感染者转化;感染者可以向治愈者转化，使得模型与实际情况更加符合，并由此我们可以得到改进的SIR模型的甲型H1N1流感防控模型的常微分方程如式1所示:

1.3 模型的求解

设日平均传染率p为1.5，易感染者的接种疫苗比例v为0.002。由于假设甲型H1N1流感潜伏期为7 d，故每日潜伏者成为传染者的比例l为1/7，每日潜伏者中转化为病毒携带者的比例q为1/6，本文中 r取估计值 0.309 4。

对改进的SIR模型，利用一般的解微分方程的方法难以求解，本文采用德国学者(Felhberg，1968)提出的四阶五级RKF算法。假设当前的步长为hk，则可以定义下面的6个ki变量:

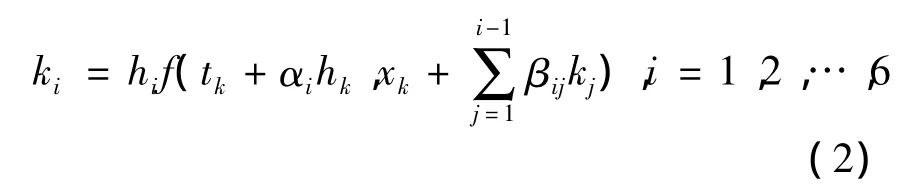
式中，tk为当前计算时刻，中间参数αi，βij及其他参数由表1(四阶五级RKF算法系数表)给出，其中αi，βij参数对又称为 Dormand-Prince对。这时下一步的状态向量可以由下式求出:

表1 四阶五级RKF算法系数表Table 1 The coefficient of four order and five stage RKF method

利用上述方法对模型进行求解，得到改进SIR模型 S(t)，I(t)，R(t)，V(t)，L(t)随时间变化的曲线图(图2)。

由图2可以看出，S(t)曲线随时间递减，表明易感染者受到传染或接种疫苗而成为潜伏者或接种疫苗者，所以数量不断减少;I(t)曲线随时间呈先递增后递减的趋势，这是由于易感染者转化为感染者，所以感染者数量逐渐增大，增大到一定值后，随着中后期防控措施的加强，感染者最终将全部转化为治愈者，直至为0;L(t)曲线随时间呈先递增后递减的趋势，这是由于潜伏者转化为确诊者，所以确诊者数量逐渐增大，增大到一定值后，随着中后期防控措施的加强，确诊者最终将全部转化为治愈恢复者，直至为0;R(t)曲线随时间呈递增趋势，这是由于确诊者不断治愈成为治愈恢复者，到最后趋于一个稳定值。V(t)曲线随时间呈递增趋势，这是由于易感染者不断接种疫苗而成为接种疫苗者。

1.4 参数修正

对日平均传染率对参数p值进行修正，再对SIR模型和改进的SIR模型进行求解。当p为1.4，1.3，1时，SIR模型和改进的 SIR 模型的 S(t)，I(t)，R(t)，V(t)，L(t)随时间变化的曲线图如图3～5所示。

由图3可以看出，随着p值的不断减小，SIR模型的S(t)曲线，I(t)曲线，R(t)曲线随时间的变化趋势不大，并且最后易感染者和感染者最后几乎都转化成了治愈恢复者，这显然与实际情况不符合，改进的SIR模型的S(t)曲线，I(t)曲线，R(t)曲线，V(t)曲线，L(t)曲线随时间呈递增或递减趋势越来越明显，这是因为:随着接触率的不断减少，以及后期防控措施的加强，易感染者数量在不断减少，接种疫苗者一直随时间呈递增趋势，这是由于易感染者不断接种疫苗，确诊者和潜伏者已与模型无关，治愈恢复者变为0。这说明所建的模型与实际情况越来越接近，模型越来越合理。

图2 防控模型的预测曲线图Fig.2 The prediction of prevention model

图3 SIR曲线图及改进SIR曲线图Fig.3 The SIR graphics and improved SIR graphics

2 基于改进SIR模型的甲型H1N1流感防控的检验

2.1 I(t)预测值与实际值的对比

当 p 为1.5，1.4，1.3，1 时，得到 SIR 模型的预测I(t)、改进的SIR模型的预测I(t)和实际I(t)随时间变化的曲线图(图4)。

由图4可以看出，当参数p逐步减小时，改进的SIR模型的预测I(t)值和实际I(t)值越来越吻合。当p值为1时，SIR模型的预测I(t)值却与实际预测I(t)值存在较大的偏差，而改进的SIR模型的预测I(t)值和实际I(t)值几乎吻合，这进一步说明了改进的SIR模型的合理性。

2.2 R(t)预测值与实际值的对比

当 p 为 1.5，1.4，1.3，1 时，得到 SIR 模型的预测R(t)、改进的SIR模型的预测R(t)和实际R(t)随时间变化的曲线图(图5)。

图4 日平均感染率取不同值时感染者比例的预测值、改进后预测值和实际值的对比图Fig.4 The comparison of the infected rate of the prediction，the improved prediction and the actual with different daily average infection rate

由图5可以看出，当参数p逐步减小时，改进的SIR模型的预测R(t)值和实际R(t)值越来越吻合。当p值为1时，SIR模型的预测R(t)值却与实际预测R(t)值存在较大的偏差，而改进的SIR模型的预测R(t)值和实际的R(t)值几乎完全吻合，这也进一步说明了改进的SIR模型的合理性。

3 结论

较之一般的SIR模型，本文的人群分类更准确，因素考虑更全面。建立模型时，增加了对潜伏者、接种疫苗者的考虑，并将甲型H1N1流感患者在发病前一天即具有传染性这一因素也考虑了进去，使得所建模型更合理，所得结果与实际情况更一致。但由于没有隐性传染者相关数据的支持，所以无法获得隐性传染者与其他人群间的转换关系，故未将其列入所建数学模型中，这也成了模型的一大缺点。

图5 日平均感染率取不同值时治愈者比例的预测值、改进后预测值和实际值的对比图Fig.5 The comparison of the cured rate of the prediction，the improved prediction and the actual with different daily average infection rate

霍阔，李世霖.2010.甲型H1N1流感传播的SIR模型研究［J］.湖南工业大学学报，24(4):40-42.

姜启源，谢金星，叶俊.2003.数学模型［M］.北京:高等教育出版社.

刘来福，曾文艺.1997.数学模型与数学建模［M］.北京:北京师范大学出版社.

李伟.2004.关于SARS病毒传播的数学模型［J］.毕节师范高等专科学校学报，22(2):46-52.

李建奎，刘天喜.2004.SARS病毒传染的数学模型［J］.科技情报开发与经济，4(2):163-164.

宇永仁.2005.SARS传播模型及其对经济的影响［J］.辽宁大学学报，32(1):1-2.

王汝发.2004.SARS传播的数学模型分析［J］.数理医药学杂志，17(2):99-100.

周永卫，范贺花.2007.传染病数学模型的马尔可夫骨架过程建模［J］.安阳师范学院学报，(2):33-35.

Fehlberg E.1968.Classical fifth-，sixth-，seventh-，and eighth-order Runge-Kutta formulas with stepsize control［R］.NASA Technical Report，287:87.