广义 Sobolev空间（T）在 Sq（T）尺度下的概率与平均 Kolmogorov宽度问题

毕 艳, 陈广贵, 徐艳艳, 甘 莹

（西华大学 数学与计算机学院,四川 成都610039）

1 引言与预备知识

众所周知,计算机所使用的计算资源非常有限,因此,在解决问题的众多算法中寻求最小计算成本的算法就尤为重要.算法的误差和成本的不同定义导致了不同的框架（或称为计算模型）:最坏情形的框架（或一致框架）、平均框架和概率框架.在最坏情形的框架下,成本和误差是通过函数类中的“最坏”的元素的特征来定义的.因此,在综合计算成本的条件下,最优误差算法是对于“最坏”元素产生最优逼近,而对于大多数元素来讲,最优误差算法所产生的逼近误差可能不是最优的,为了解决这一问题,我们通常考虑在函数集上定义一概率测度,考虑其平均误差和概率误差.平均误差给出了函数类在给定的测度下的逼近度的平均,反映了在一定的计算成本下大多数元素的最小误差,它更为深刻地反映了函数类结构的本质特征.概率误差则进一步给出了达到某个误差阶的元素在给定的测度下的分布,更深刻的刻画了函数类的内在结构特征.特别地,在最优算法的研究中,要确定最坏框架、平均框架、概率框架下的最优误差阶,往往是通过计算相应情形下的函数集宽度而得到.

X是具有范数‖·‖线性赋范空间,W是X的有界子集,FN是X上的N-维子空间.定义W对FN的偏差为

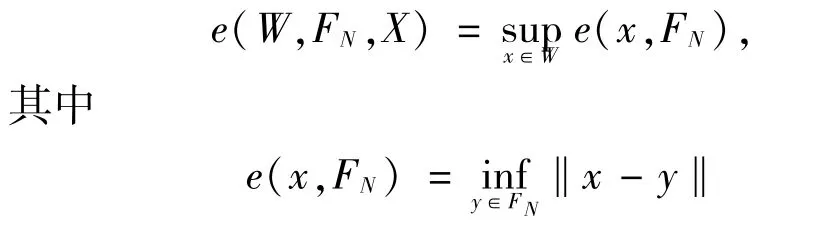
是FN对x的最佳逼近.因此,W在X空间中的Kolmogorov N-宽度定义为

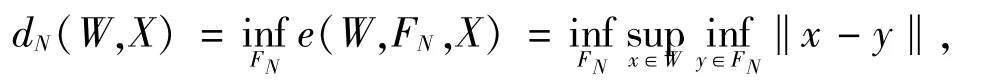
其中,FN取遍X中维数不超过N的所有线性子空间.

设W的子集B是由W中的开子集所生成的Borel域,μ是B上概率测度,也就是说μ是B上的σ-非负可加的函数,且μ（W）＝1.记δ∈（0,1）的任意实数,则W在X空间中关于测度μ的Kolmogorov概率（N,δ）-宽度定义为

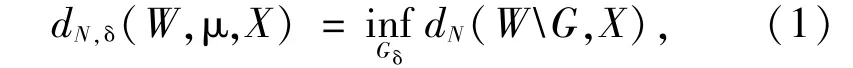
其中,Gδ取遍B中测度不超过δ的所有线性子空间.

定义W在X空间中关于测度μ的Kolmogorov p-平均N-宽度为

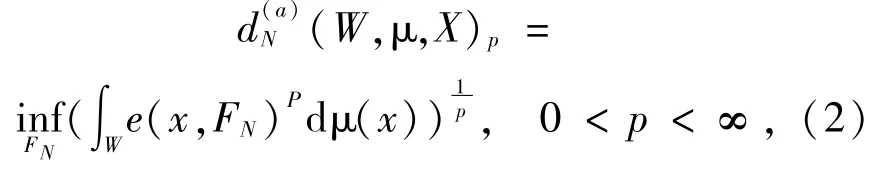
其中,（2）式中的FN取遍X中维数不超过N的所有线性子空间.

经典的N-宽度在最坏框架下,用某种意义下的最优逼近工具给出这类函数的最优恢复,宽度值即对于“最坏”元素的最佳逼近的误差估计.然而,经典的宽度未能给出对于大多数元素的误差估计,这也反映在对于大多数元素来说最佳逼近的误差值一般小于经典宽度值,无论从实际应用还是理论分析的角度,研究全空间的逼近性质都是很重要的.因此,如何在经典宽度的基础上拓广宽度的概念,使之发挥更大的作用是至关重要的.于是引入了概率宽度和平均宽度的概念.概率宽度也刻画了最佳逼近误差,它的误差则是由测度至少为1-δ的子集在最坏情况下定义的,反映了W的所有子集最佳逼近的μ分布,给出了达到某个误差阶的元素在给定测度下的分布,更为深刻的刻画了函数类的内在结构特征.平均宽度所刻画的最佳逼近误差是由误差在给定的测度下的积分定义的,它反映了空间大多数元素的最优逼近.关于经典宽度的相关知识可参阅文献［1-4］,而关于概率宽度与平均宽度可参阅文献［5-17］.

令Lq（T）,1≤q≤∞,表示周期为 2π的 q次Lebesgue 可积函数类,且‖· ‖Lq（T）为其上范数.令x（t）,t∈［0,2π］为 Hilbert空间 L2（T）上的 2π为周期的函数,则有

2 主要结果

3 离散化

4 主要结果的证明

这样就完成了定理2的证明.

致谢西华大学研究生创新基金（04030209）对本文给予了资助,谨致谢意.

［1］ Pinkus A.n-widths in Approximation Theory［M］.Berlin:Springer-Verlag,1985:1-150.

［2］ Temlyakov V N.Approximation of functions with bounded mixed derivative［J］.Tr Mat Inst Akad Nauk SSSR,1986,178:1-112.

［3］ Traub J F,Wasilkowski G W,Wozniakowski H.Infirmation Based Complexity［M］.New York:Academic Press,1988:55-70.

［4］ Traub J F,Wozniakowski H.A General Theory of Optimal Algorithms［M］.New York:Academic Press,1980:5-80.

［5］ Maivorov V E.Widths of spaces,endowed with a Gaussian measure［J］.Russion Acad Sci Dokl Math,1992,45:305-309.

［6］ Maivorov V E.Kolmogorov's （n,δ） -widths of the spaces of the smooth functions［J］.Russion Acad Sci Sb Math,1994,79:265-279.

［7］ Maivorov V E.Linear widths of functions spaces equipped with the Gaussian measure ［J］.J Approx Theory,1994,77:74-88.

［8］ Maivorov V E,Wasilkowski G W.Probabilistic and average linear widths in L∞-norm with respect to r-fold Wiener measure［J］.J Approx Theory,1996,84:31-40.

［9］ Ritter K.Average Case Analysis of Numerical Problems,Lecture Notes in Maths［M］.Berlin:Springer-Verlag,2000:1733.

［10］ Sun Y S.Average n-width of point set in Hilbert space［J］.Chinese Sci Bull,1992,37:1153-1157.

［11］ Sun Y S,Wang C Y.μ-average widths on the Wiener space［J］.J Complexity,1994,10:428-436.

［12］ Sun Y S,Wang C Y.Average error bounds of best approximation of continuons functions on the Wiener space ［J］.J Complexity,1995,11:74-104.

［13］ Kuo H H.Gaussian Measure in Banach Space in Lecture Notes in Mathematics［M］.Berlin:Springer-Verlag,1975:463.

［14］ Ledoux M,Talagrand M.Probability in Banach Space［M］.Berlin:Springer-Verlag,1991:23.

［15］陈广贵,蔡斌畏.无限维空间在概率框架和平均框架下的逼近特征［J］.西华大学学报:自然科学版,2011,30（5）:25-28.

［16］张健,舒级.低维空间中带调和势的非线性Schrö dinger方程［J］.四川师范大学学报:自然科学版,2002,25（3）:226-228.

［17］张亚兰,陈广贵,罗新建.多重调和基样条对多元带有限函数的恢复［J］.四川师范大学学报:自然科学版,2010,2:176-178.