修改的（G′/G）-展开方法与Sharma-Tasso-Olver方程的行波解

马志民, 孙峪怀

（1.成都理工大学 工程技术学院基础部,四川 乐 山614000； 2.四川师范大学 数学与软件科学学院,四川 成 都610066）

形如

的Sharma-Tasso-Olver方程［1-2］,首次是由A.S.Sharma和H.Tasso［1］作为Burgers方程族的一个推广提出的,这里α是任意实数,u（x,t）是依赖时间变量t和空间变量x的未知函数.该方程作为一个重要的数理模型,引起了数理学家们的广泛关注.文献［3-6］探讨了Sharma-Tasso-Olver方程的对称性并构造了该方程的一些孤立波解和周期解,其中在文献［6］中还讨论了寻找Sharma-Tasso-Olver方程行波解中常见的几种问题.近年来,已经有许多有效的方法［7-16］应用在非线性偏微分方程行波解的构造中,如推广的Riccati方程法［7-8］、广义的辅助微分方程法［9］、试探函数法［10］、其次平衡法［11］和定性理论的相平面分析法［12］等.在2008年,M.L.Wang等［13］提出了一种名为（G′/G）-展开法来构造非线性偏微分方程的行波解.利用此方法,许多非线性偏微分方程的行波解［14-15］已经被获得.此后,A.R.Shehata［16］对（G′/G）-展开法做了修改,使这一修改方法获得的行波解结构更为广义,也更符合物理背景.下面先将介绍这种修改的（G′/G）-展开法构造非线性偏微分方程的行波解的具体过程.

1 修改的（G′/G）-展开方法的描述

考虑下面的非线性偏微分方程

其中,ai（i＝0,1,2…）,c是待定量,正整数m可以通过平衡方程（3）中的最高次耗散项和最高次非线性项来确定,G满足如下的常微分方程

其中,λ、μ是常数.

将（4）式代入到方程（3）,然后令（G′/G）i（i＝1,2,…,m）的各次幂系数为零,得到一个关于ai、c的代数方程组.借助Maple求解这个代数方程组,并利用方程（5）的解［15］,获得方程（2）的行波解.下面具体应用此方法来探讨Sharma-Tasso-Olver方程.

2 方程（1）的解

要得到方程（1）的解,首先将变换

借助Maple解上面的代数方程组,得到a-1、a0、a1和c为如下的结果:

结果1:a-1＝-μ,a0＝0,a1＝1,c＝α λ2-4α μ；

结果2:a-1＝0,a0＝λ,a1＝2,c＝α λ2-4α μ；

结果3:a-1＝-2μ,a0＝-λ,a1＝0,c＝α λ2-4α μ.这里,令Δ＝λ2-4μ.

将结果1代入到（8）式,从而得到方程（1）有如下形式的解:

情况1当Δ＞0,方程（1）有如下的双曲函数形式解

情况2当Δ＜0,方程（1）有如下的三角函数形式解

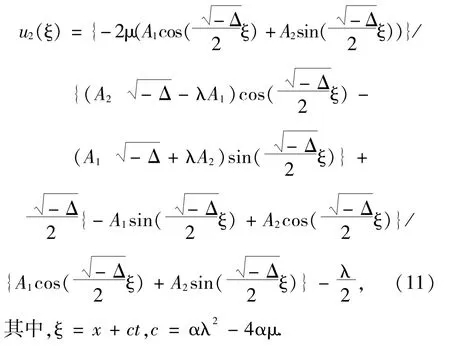
情况3当Δ＝0,方程（1）的解没有意义.

将结果2代入到（8）式,从而得到方程（1）有如下形式的解.

情况4当Δ＞0,方程（1）有如下的双曲函数形式解

情况5当Δ＜0,方程（1））有如下的三角函数形式解

情况6当Δ＝0,方程（1）的解没有意义.

将结果3代入到（8）式,从而得到方程（1）有如下形式的解.

情况7当Δ＞0,方程（1）有如下的双曲函数形式解

情况8当Δ＜0,方程（1）有如下的三角函数形式解

情况9当Δ＝0,方程（1）的解没有意义.

3 结论

通过使用修改的（G′/G）-展开法得到了广义Sharma-Tasso-Olver方程的多种新的行波解,在对其中一些解的相关系数做特殊的变换后可以得到了几种孤立子解形式.在这些结果中u3和u4与文献［4］是类似的,但u1、u2、u5和u6还没有在其它文献中出现过.由上述可知该方法对Sharma-Tasso-Olver方程行波解的构造是非常有力的.

［1］ Sharma A S,Tasso H.Connection between wave envelope and explicit solution of a nonlinear dispersive equation ［R］.Repot IPP,1974:6/158.

［2］ Olver P J.Evolution equations possessing infinitely many symmetries［J］.J Math Phys,1977,18（6）:1212-1215.

［3］ Lian Z J,Lou S Y.Symmetries and exact solutions of the Sharma-Tass-Olver equation［J］.Nonlinear Anal,2005,63:1167-1177.

［4］ Shang Y D,Qin J H,Huang Y,et al.Abundant exact and explicit solitary wave and periodic wave solutions to the Sharma-Tasso-Olver equation［J］.Appl Math Comput,2008,202（2）:532-538.

［5］ Ma W X,Chen M.Do symmetry constraints yield exact solutions［J］.Chaos,Solitons ＆ Fractals,2007,32（4）:1513-1517.

［6］ Kudryashov N A.Seven common errors in finding exact solutions of nonlinear differential equations ［J］.Commun Nonlinear Sci Num Simulat,2009,14（9/10）:3507-3529.

［7］洪宝剑,卢殿臣,张大珩.带强迫项变系数组合KdV-Burgers方程的显式精确解［J］.广西师范大学学报:自然科学版,2007,25（1）:17-20.

［8］孙峪怀,杨少华,王佼,等.非线性Chaffee-Infante反应扩散方程的新精确解［J］.四川师范大学学报:自然科学版,2012,35（3）:293-296.

［9］ Sun Y H,Ma Z M,Li Y.Explicit solutions for generalized（2+1） -dimensional nonlinear Zakharov-Kuznetsov equation［J］.Commun Theory Phys,2010,54（3）:397-400.

［10］赵云梅.利用试探函数法求耦合KdV方程组的精确解［J］.四川师范大学学报:自然科学版,2012,35（6）:746-748.

［11］曹瑞,张健.一类非线性方程的显示精确解［J］.四川师范大学学报:自然科学版,2007,30（2）:131-133.

［12］ Ma Z M,Sun Y H,Liu F S.Explicit solutions and bifurcations for a class of generalized boussinesq wave equation ［J］.Commun Theory Phys,2013,59（3）:307-310.

［13］ Wang M L,Li X Z,Zhang J.The （G′/G） -expansion method and travelling wave solutions of nonlinear evolution equations in mathematical physics［J］.Phys Lett,2008,A372（4）:417-423.

［14］李灵晓,张金良.扩展的（G′/G）-展开法和gZK方程的精确解［J］.四川师范大学学报:自然科学版,2010,33（5）:626-629.

［15］马志民,孙峪怀,孙阳,等.广义变系数Gardner方程新的精确解［J］.四川师范大学学报:自然科学版,2012,35（4）:435-438.

［16］ Shehata A R.The traveling wave solutions of the perturbed nonlinear Schr ö dinger equation and the cubic-quintic Ginzburg Landau equation using the modified （G′/G）-expansion method［J］.Appl Math Comput,2010,217（1）:1-10.