同杆并架双回线故障测距的新算法

陈坤燚，钟建伟

(湖北民族学院信息工程学院，湖北恩施445000)

同杆并架双回线具有输送容量大，占地少，出线走廊窄，建设快，投资少等一系列优点，目前在高压、超高压输电中已经得到了广泛的使用.准确，可靠的故障测距，对恢复供电、提高经济效益以及对系统的安全稳定有着重要意义.然而，由于同杆并架双回线是两回线路共用一杆塔，线间距离较近，故障类型不仅仅是相间和接地故障，还会存在一系列复杂的跨线故障，导线间不仅仅存在相间耦合关系，而且还存在线间的耦合关系，因而，同杆并架双回线测距有其特殊性.

在同杆双回线测距方面，众多学者作出了大量卓有成就的研究，提出了很多同杆双回线的测距算法.文献［1］提出了一种使用单端工频电气量进行故障测距的算法，该算法适用于单线故障;文献［2］采用分布参数，利用双端数据提出了一种在准确参数未知时的故障测距新方法;文献［3］利用故障点处同向正序电流与反向正序电流的特殊关系来进行故障测距，该方法适用于单线故障;文献［4］将同杆双回线的故障分为四种类型，提出了一种单端测距的算法;文献［5］该文献基于线路分布参数，利用环流网，提出了一种单端工频电流量的测距算法;文献［6］根据双回线环流网两端电压为零的特点，提出了一种利用双端非同步电流时限测距的时域方法;文献［7］利用同反相序网，并利用最小二乘法，提出了一种单端测距算法;文献［8］基于RL模型提出了一种单端时域测距算法，该方法是通过计算故障相的沿线电压，并利用边界条件进行测距;文献［9］提出了一种基于故障线双端电气量的故障测距方法，该方法适用于单线故障.从众多学者的研究来看，单端测距只采用一端数据，但受对称系统阻抗、过渡电阻的影响较为严重;双端测距引入了双端电气量，能够从原来上避免过渡电阻和系统阻抗的影响.从解耦方法来看，目前较多的算法采用的是六序分量法，其中，反相环流网有其两端电压为零的优点，而被广大学者青睐，用它来构造测距算法，取的了很好的效果，但因为在发生对称性跨线故障时环流网不存在，从而造成无法测距.再者，六序分量法的应用，要求线路完全换位，双回线参数完全相同，否则，用六序分量法测距就会存在较大的误差.

本文基于集中参数模型，从双回线的电磁耦合关系入手，计算各相沿线电压分布，利用从双端计算电压分布在故障点处电压相等这一原理构造测距算法.该算法从线路的电磁耦合关系直接入手，对于各种单线故障和各种跨线故障都能够较为准确的测距;避免了使用六序分量法解耦，对不完全换位的线路任然适用;利用两端的数据，从原理上避免了过渡电阻和系统阻抗的影响;在构造测距方程时，采用的是两端的模量，从而避免了双端数据同步的影响.PSCAD仿真表明，该算法对各种故障都有较为理想的测距精度，能够满足同杆并架双回线的测距要求.

1 沿线电压分布计算

设I回线和II回线的单根导线的阻抗为z，相间互阻抗为 zm，线间互阻抗为分别为第 I回线、第 II回线故障点处的三相电压矩阵分别为 M、N 端母线三相电压矩阵分别为第 I回线、第 II回线M端电流矩阵分别为第 I回线、第 II回线 N 端电流矩阵，忽略分布电容的影响，则在距离M端母线x处的各相电压可用如下式子来表示:

图1 同杆并架双回线简化系统图Fig.1 The simplified system of double circuit line on same tower

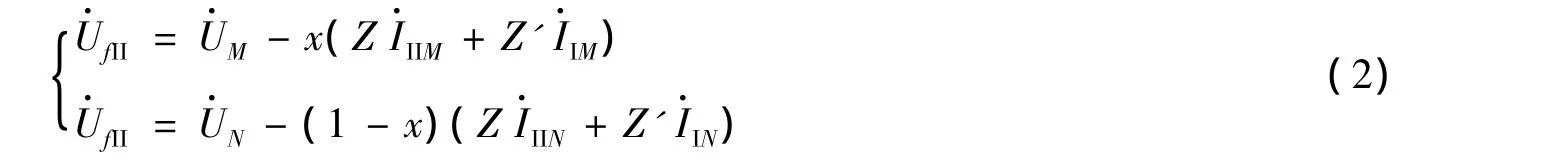
式中:i=Ι、ΙΙ，j=M、N.

根据式(3)，则式(1)、(2)可改写成:

以上式(4)、(5)两式即为沿线故障分量电压计算公式，无论线路是否发生故障，两式总是成立的，无论是哪回线、哪一相发生故障，两式也总是成立的.

2 故障测距算法和数据同步

2.1 故障测距方程

对于线路中的某一点，无论是从线路M端，还是从N端进行计算，这一点的对地电压都应该是相同的，所以根据式(4)、(5)可得:

对式(7)、(8)两式进行变换，可得:

由于式(9)、(10)两式不管在什么情况下，总是成立的，因此，当发生故障时利用其中之一都能够计算出故障点的位置x.

2.2 测距方程分析

分析式(9)、(10)，不难发现，两式对应着6个方程，每个方程都可以解出一个x，下面将对各种类型的故障情况下方程的解分别进行讨论.

1)单回线发生接地短路以及三相不接地短路 不妨设I回线A相发生单相接地短路，如果忽略分布电容的影响(以下分析均未考虑电容的影响，不再做说明)，则此时流过I回线A相的故障电流方向为母线指向故障点.I回线的BC相以及II回线的ABC相，流过的故障电流为零.如果用式(9)进行测距计算，则可以写成:，则可以解出3个x;如果用式(6)进行测距计算，则可以写成:，可以解出3个x.当单回线发生两相或三相接地短路以及三相不接地短路时，情况与单相接地一样，这里不在分析.所以，当单回线发生接地故障时，无论是I回线还是II回线，用式(9)或式(10)都能够计算出故障位置.

2)单回线发生相间不接地短路 不妨设I回线BC相在非母线处发生不接地短路，则此时流过I回线B相的故障电流与流过I回线C相的故障电流幅值相等，相位相反，其他相故障电流基本为零.如果用式(9)来计算故障，则也可以写成:，从式中可以看出，由于，故如果用式(9)中的第一个方程无法计算故障距离，而用第二或第三个等式，则能够算出故障位置;但如果用式(10)，由于I回线B相电流与I回线C电流幅值相等，相间相差180°，且I回线A相故障电流为零，故式(10)的左边项等于零，故无法算出故障距离.从上面分析可以看出，当发生单回线相间不接地短路时，需要用故障线的计算式才能准确算出故障位置.

3)发生跨线短路 当线路发生跨线故障时，I回线和II回线的三相故障电流至少有一相不为零，即，矩阵全为非零阵，所以，无论用式(9)，还是式(10)，都能计算出故障的位置.

综上所述，当系统发生接地性短路时，用式(9)、(10)中的任何一个等式都能够进行测距计算;当发生单线相间短路时，则需要与相应故障线路的测距方程进行测距计算，才能准确的算出故障的位置.

4)一回线运行另一回线挂地检修 不妨设I回线运行，II回线挂地检修.在这种运行方式下，当I回线发生短路时，流过II回线的故障电流为零，即全为零阵，而流过I回线的故障电流为非零，即，全为非零阵，所以，测距方程(9)可改写成:

2.3 故障测距算法

从前面的分析，可知，由于发生单回线相间短路时，只有用相应线路的测距方程才能准确计算出故障点的位置，所以，在进行故障点位置计算前，应线选出故障线，然后在进行计算.相间故障时，算出的3个x值，有一个是不准确的，因此，我们就取两个比较接近的值作为故障点的位置.当发生其他类型的故障时，无论用两式(9)还是式(10)，都能准确算出故障点的位置.测距算法的流程图如图2所示.

2.4 双端数据同步

在双端测距算法中，如果两端数据采集不同步，将影响测距的精度.但两端数据是否同步，只会影响相角，而不会影响幅值，所以，将式(9)、(10)两式改为如下形式，则可不受数据是否同步的影响.

求解式(11)或式(12)，则可算出故障距离x，但式(11)、(12)两式是一元二次方程，可以用二分法或者牛顿迭代法求解，本文采用二分法求解.

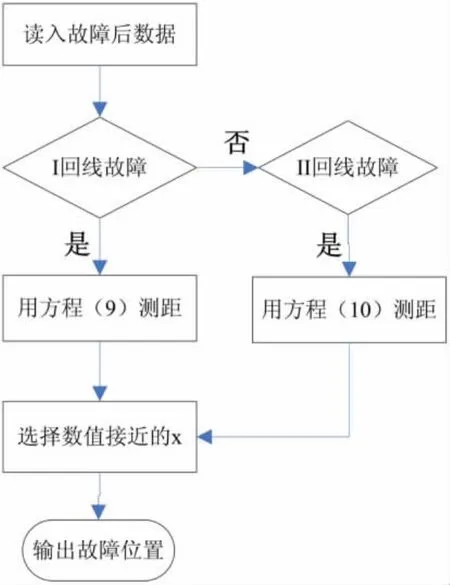
图2 故障测距流程图Fig.2 The process of fault location

3 仿真验证

本文采用如图3所示的仿真模型，用PSCAD和MATLAB进行仿真，该模型M、N两端的电压等级为500 kV，线路全长100 km.

M 端系统参数:Zm1=Zm2=20.84∠83.11°，Zm0=19.623∠83.86°

N 端系统参数:Zn1=Zn2=35.79∠80.38°，Zm0=45.28∠79.22°，

两侧的电势角差为30°.

线路参数:

导线阻抗:z=6.0183 ×10－5+j5.2533 ×10－4Ω/km

相间互阻抗:zm=4.1591 ×10－5+j2.6169 ×10－4Ω/km

线间互阻抗:z′m=1.5162 ×10－5+j4.7818 ×10－5Ω/km

正序对地电容:C1=1.095 ×10－2μF/km

零序对地电容:C0=5.473 ×10－3μF/km

双回线间零序电容:C′0=2.600 ×10－3μF/km

表1为在线路20%和60%处发生金属性短路时的仿真结果，表2为在线路20%和60%处发生经300Ω电阻接地短路时的仿真结果，表3为I回线运行II回线两端挂地检修时的仿真结果.

图3 仿真系统接线Fig.3 The simulation network

表1 仿真结果ATab.1 The simulative result A

从表1和表2的计算结果可知:此算法对各种单线故障以及各种对称性和非对称性跨线故障均能准确的测距，具有较高的精度，且不受过渡电阻的影响;从表3可以看出，在一回线挂地检修另一回线运行时也能够准确测距，该算法解决了运行方式对测距算法的影响.

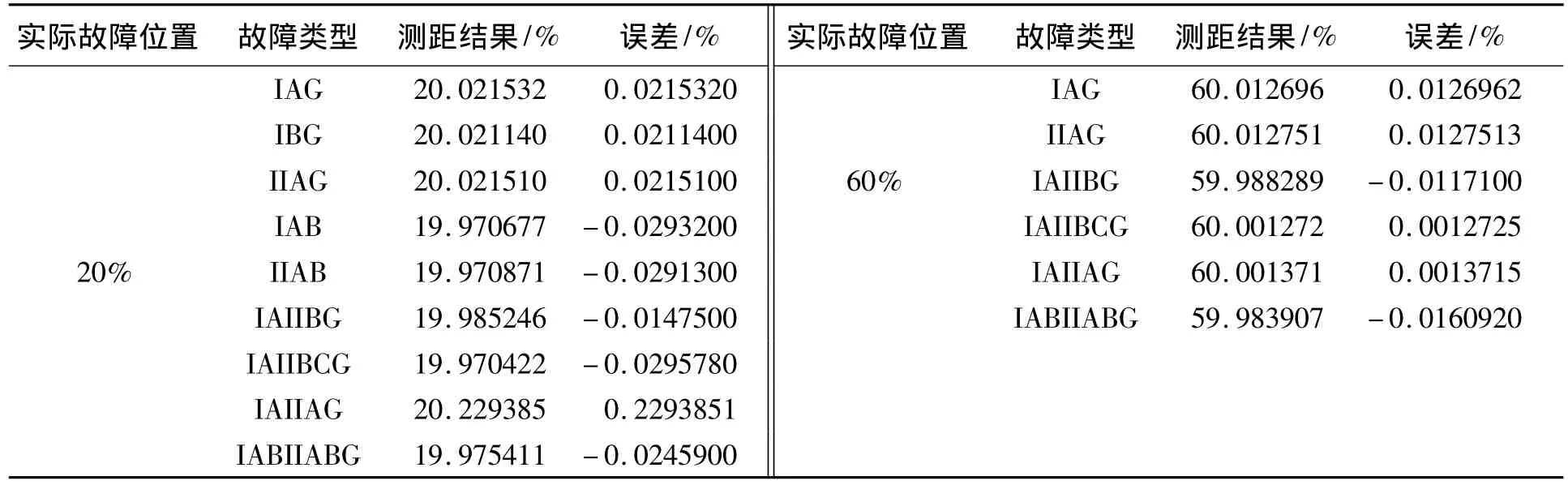
表2 仿真结果BTab.2 The simulative result B

表3 仿真结果CTab.3 The simulative result C

4 结论

本文从线路的耦合关系入手提出了一种双端故障测距算法，测距方程是用双端模量构造的，不受双端数据同步的影响，对于单线故障、各种对称性和非对称性跨线故障均能准确的测距，从仿真结果来看，本算法不受过渡电阻的影响，并有较为理想的精度;对于一回线运行另一回线挂地检修的双回线运行状态，本算法也能够精确的测距;如果在线路参数不对称的情况下，只需要修改阻抗矩阵，则任然可以测距.本文所提出的方法是采用集中参数模型，与采用分布参数模型算法相比较，算法的计算量大为减小，但同样具有较高的精度.

［1］ 索南加乐，吴亚萍，宋国兵.基于分布参数的同杆双回线单线故障准确测距原理［J］.中国电机工程学报，2003，23(5):41－43.

［2］ 赵永娴，曹小拐，刘万顺.同杆并架双回线准确参数未知时的故障测距新方法［J］.电力系统自动化，2005，29(4):72－76.

［3］ 龚震东，范春菊，郁惟镛.一种基于六序网图的同杆双回线故障测距算法［J］.电力系统自动化，2007，31(17):58－60.

［4］ 李红巍.一种实用的双回线测距方法［J］.电力系统自动化，1995，19(9):30－33.

［5］ 索南加乐，王树刚，张超.利用单端电流的同杆双回线准确故障定位研究［J］.中国电机工程学报，2005，25(23):25－30.

［6］ 索南加乐，宋国兵，许庆强.利用两端非同步电流的同杆双回线故障定位研究［J］.中国电机工程学报，2004，19(8):99－106.

［7］ 束洪春，刘振松，彭仕欣.同塔双回线电弧故障单端测距算法［J］.电力自动化设备，2004，19(8):99－106.

［8］ 宋国兵，穆国强，崔琪.基于RL模型的双回线单端时域法故障定位［J］.电力系统保护与控制，2009，37(20):34－42.

［9］ 刘千宽，李永斌，黄少锋.基于双端电气量的同杆平行双回线单线故障测距［J］.电网技术，2008，32(3):27－30.