长江日径流序列的多重分形性质研究

唐 强，胡铁松

(1.武汉纺织大学数学与计算机学院，湖北武汉430200;2.武汉大学水资源与水电工程科学国家重点实验室，湖北武汉430072)

自20世纪70年代Mandelbrot提出分形理论以来，分形理论在自然科学和社会科学，包括水文水资源领域有着广泛的应用［1－3］.日径流序列的变化特征是水文分析的研究重点之一，许多学者将分形理论应用于其中.侯玉等用分形理论对洪峰散点序列进行了分析，发现洪峰散点序列在一定尺度范围内表现出了自相似性，初步证明洪峰散点序列是一种分形［4］.刘德平用盒子数法计算了日流量过程线的分形维数，并讨论了分维与形状因子的关系［5］.丁晶和刘国东用盒子数法计算了汛期日流量过程线的分形维数［6］.李贤彬用小波分析法计算了汛期日流量过程的分形维数［7］.但是对于径流这样的复杂系统，仅用单一分形维数来加以描述是远远不够的，不能反映径流序列变化的精细结构.常福宣分析了金沙江屏山站和岷江紫坪铺站日径流过程的分形特性，结果表明，单一的分形维数不能完全描述日流量在时间上的分布特性，必须应用多重分形法来研究径流过程特征［8］.本文详细讨论了长江宜昌站1950年至1999年日径流序列的多重分形性质，结果表明，不论是长期(50年)还是短期(1年)，长江日径流序列均具有多重分形性质，这将为多重分形在日径流非线性性质方面的研究提供重要的理论基础.

1 多重分形理论

多重分形是定义在分形结构上的由有限几种或大量具有不同奇异标度指数α的概率子集构成的非均匀分布的奇异集合［9］.多重分形通过奇异谱函数f(α)来定量刻画分形体由不同局部条件、或在演化过程中不同层次所导致的概率Pi在整个集合上的分布状况，是对分形结构复杂程度、不规则程度以及不均匀程度的度量［10－13］.

设要研究的日径流序列为{X(t):t∈［0，T］}.首先用尺度ε将时间区间［0，T］分割成一些不相交的子区间.令Pi(ε)是时间标度为ε时第i个区间径流量之和的归一化流量(概率测度)，即:

其中Ii是时间标度为ε的第i个区间的径流量之和，∑iPi(ε)=1.定义配分函数χq(ε)为Pi(ε)的q阶矩:

这里q为权重因子，χq(ε)反映了Pi(ε)的不均匀性.当q≫1时，大的Pi(ε)对χq(ε)的贡献占优势;当q≪ －1时，小的Pi(ε)对χq(ε)的贡献占优势，因此χq(ε)给出了Pi(ε)的另一种分布形式.对于满足多重分形特征的时间序列而言，配分函数χq(ε)和ε有如下的幂函数关系成立，即:

其中τ(q)为质量指数，定义如下:

实际计算中可通过lnχq(ε)～lnε双对数曲线中无标度区(即线性区间)的点进行最小二乘拟合来估算.如果时间序列具有多重分形性质，τ(q)应为q的非线性函数;如果时间序列只有单分形性质，则τ(q)是q的线性函数.进一步，由τ(q)可定义广义分形维数Dq:

质量指数τ(q)和广义分形维数Dq构成了描述多重分形的一套重要的参量.除此之外，若时间序列满足多重分形特征，则:

其中α称为奇异性指数，是反映各小区间奇异程度的度量.如果对所有的小区间，α取值相同，则时间序列为单分形;否则为多重分形.记具有相同α值的区域数为Nα(ε)，则对于多重分形，有:

其中f(α)表示具有相同α值的子集的分形维数.一个复杂的分形体的内部可以分为一系列不同α值所表示的子集，这样f(α)就给出了这一系列子集的分形特征，称函数f(α)为多重分形谱或奇异谱，通常为光滑的单峰函数.f(α)给出了比简单分维更丰富的结构信息.例如大的α反映的是小概率测度区间的性质;小的α则反映的是大概率测度区间的性质;多重分形谱的宽度△α=αmax－αmin的大小反映了整个分形结构上概率测度分布的不均匀程度.因此f(α)是对分形结构上的复杂程度、不规则程度以及不均匀程度的一种度量.α和f(α)构成了另一套描述多重分形的重要的参量，它们和τ(q)之间满足如下关系:

2 长江屏山站日径流序列的多重分形研究

本文讨论的数据为长江宜昌站1950年至1999年的日径流时间序列.对于这50年共18359个数据，首先计算其配分函数χq(ε)和质量指数τ(q).理论上q的取值范围为(－∞，+∞)，但在实际计算中q值不可能是无限大.经计算发现，当|q|从60增加到70时，Dq的变化很小，因此本文|q|的最大值取60.图1是在q取不同值时的lnχq(ε)～lnε曲线簇，从图1中可看出q取不同值时，lnχq(ε)～lnε均有良好的线性关系(如q=60时，相关系数为0.9958)，表现出很好的标度不变性.对lnχq(ε)～lnε双对数曲线中的点进行最小二乘拟合即可求得质量指数τ(q).从图2可看出，τ(q)是一个凹向横轴的非线性函数，表明该日径流时间序列具有多重分形性质.

得到τ(q)之后，由式(5)、(8)、(9)即可求得广义分形维数Dq、奇异性指数α和多重分形谱f(α).从图3、4可看出，随着q的增加，Dq逐渐减小，最后稳定在0.7486左右.对于不同的q值，Dq是不一样的，说明该日径流时间序列具有明显的多重分形性质.盒维数D0、信息维数D1和关联维数D2均不相等，满足D0＞D1＞＞D2.f(α)曲线是一条单峰曲线，呈右钩状，最大值 fmax=0.999 6 即为盒维数 D0，其相关参数 αmin，αmax，△α=αmax－αmin，f(αmin)，f(αmax)，△f=f(αmin)－f(αmax)，见表1.由f(α)的定义，f(αmin)表征了概率测度最大子集的数目，而f(αmax)表征了概率测度最小子集的数目，故△f＜0意味着最小概率子集占据主导地位，即在该日径流时间序列中更多时间径流量较低.

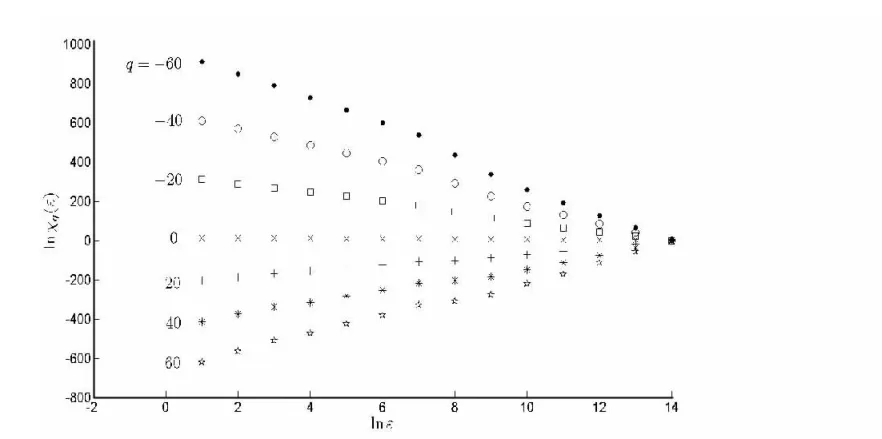
图1 日径流时间序列的lnχq(ε)～lnε曲线簇Fig.1 χq(ε)versus ε in logarithm(base 2)of the daily runoff series

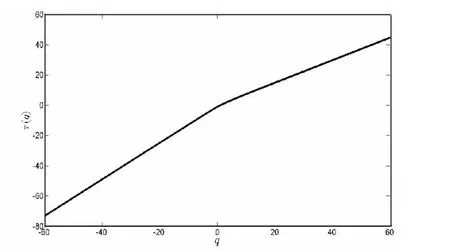
图2 日径流时间序列的τ(q)曲线Fig.2 The τ(q)curve of the daily runoff series

图3 日径流时间序列的Dq曲线Fig.3 The Dqcurve of the daily runoff series

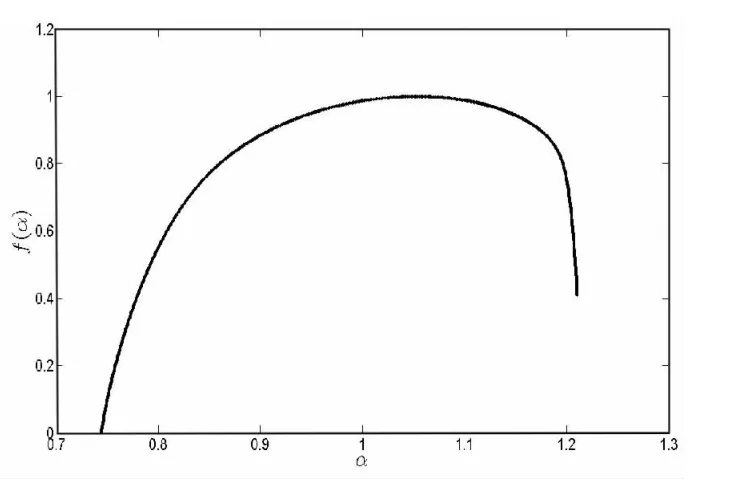
图4 日径流时间序列的f(α)曲线Fig.4 The f(α)curve of the daily runoff series

进一步还讨论了每一年日径流序列的多重分形性质.类似于上述做法，求出了每一年日径流序列的质量指数τ(q)、广义分形维数Dq、奇异性指数α、多重分形谱f(α).从 τ(q)、Dq和 f(α)可看出，每一年日径流序列均有明显的多重分形性质(篇幅所限，只给出了1975年、1980年和1989年的τ(q)、Dq和f(α)曲线图以及多重分形谱的相关参数，见图5、图6、图7和表2).因为△α的大小反映了整个分形结构上概率测度分布的不均匀程度，而1975年日径流序列的△α=0.6195最大，1989年的△α=0.2951最小，说明1975年日径流量涨落幅度最大，1989年日径流量涨落幅度最小.50年中仅有11年的△f＞0，其他年份的△f＜0，说明大多数年份日径流时间序列中更多时间径流量较低.

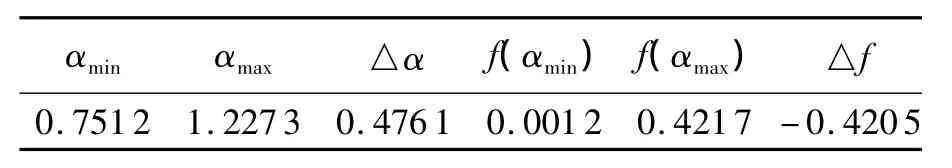
表1 图4中多重分形谱的主要参数Tab.1 Main multifractal parameters of fig 4

图5 三年日径流时间序列的τ(q)曲线Fig.5 The τ(q)curve of 1975，1980 and 1989 annual series

图6 三年日径流时间序列的Dq曲线Fig.6 The Dqcurve of 1975，1980 and 1989 annual series

图7 三年日径流时间序列的f(α)曲线Fig.7 The f(α)curve of 1975，1980 and 1989 annual series

3 结语

本文分析了长江宜昌站1950年至1999年长期(50年)日径流时间序列和短期(每年)日径流时间序列的多重分形性质.结果表明，50年日径流时间序列和每年日径流时间序列均具有明显的多重分形特性，大多数年份日径流时间序列中更多时间径流量较低.多重分形可以揭示日径流时间序列的分形测度的非均匀特征，为研究长江日径流的变化特征提供了更多的信息，对于研究长江日径流的非线性性质提供了重要的理论基础.

表2 三年日径流时间序列多重分形谱的主要参数Tab.2 Main multifractal parameters of 1975，1980 and 1989 annual series

［1］ Gupta V K.Statistical self－similarity in river networks parameterized by elevation［J］.Water Resources Bulletin，1989，25(3):72 －75.

［2］ 李新杰，胡铁松，郭旭宁，等.0－1测试方法的径流时间序列混沌特性应用［J］.水科学进展，2012，32(6):875－882.

［3］ 常福宣，丁晶，姚健.降雨随历时变化标度性质的探讨［J］.长江流域资源与环境，2002，11(1):79－83.

［4］ 侯玉，吴伯贤，邓国权.分形理论用于洪水分期的初步探讨［J］.水科学进展，1999，10(2):140－143.

［5］ 刘德平.分形理论在水文过程形态特征分析中的应用［J］.水利学报，1998(2):20－25.

［6］ 丁晶，刘国东.日径流过程分维估计［J］.四川水力发电，1999，18(4):74－76.

［7］ 李贤彬.子波分析及其在水文水资源研究中的应用［D］.成都:四川大学，1999:9－98.

［8］ 常福宣.分形理论在水文水资源研究中的应用［D］.成都:四川大学，2001:40－45.

［9］ Halsey T C，Jensen M H，Kadanoff L P.Fractal measures and their singularities:the characterization of strange sets［J］.Phys Rev A，1986，33:1141－1150.

［10］ Grassberger P，Procaccia I.Characterization of strange attractors［J］.Phys Rev Lett，1983，50:346 －349.

［11］ Meakin P，Stanley H E，Coniglio A，et al.Surfaces，interfaces，and screening of fractal structures［J］.Phys Rev A，1985，32:2364 －2369.

［12］ Jensen M H，Levermann A，Mathiesen J，et al.Multifractal structure of the harmonic measure of diffusion － limited aggregates［J］.Phys Rev E，2002，65:046109 －046116.

［13］ Tasinkevych M，Tavares J M，de los Santos F.Diffusion － limited deposition with dipolar interactions:Fractal dimension and multifractal structure［J］.J Chem Phys，2006，124:064706