大气压氩气介质阻挡均匀放电的数值模拟

刘富成，王晓菲

（河北大学物理科学与技术学院，河北保定 071002）

近年来，大气压非平衡等离子体因其在材料表面改性、薄膜生长、废气处理、医疗器械消毒等众多领域有着广泛的应用前景而备受人们关注［1－2］.目前产生大气压非平衡等离子体的方法有很多，其中介质阻挡放电是最为常用的一种方式.在大气压条件下，介质阻挡放电通常是以随机分布的放电丝的形式出现，然而在某些特定的条件下，它也可以呈现均匀的放电模式.自从20世纪80年代，日本的Okazaki小组在压强为1.01×105Pa下的氦气中获得了稳定的辉光放电以来，法国的Massines［3］以及美国的Roth等［4］研究小组分别利用介质阻挡放电结果实现了大气压氩气、氮气、氧气以及空气等辉光放电.

对于大气压辉光放电的成因问题，Roth等人［4］首先提出了离子俘获机理的理论，然而清华大学的王新新等人［5］根据实验结果对该理论提出了质疑.为了更好地揭示大气压均匀放电的产生机理，多个小组对大气压氦气和氮气均匀放电进行了相应的数值模拟.结果发现，大气压氦气均匀放电呈现辉光放电模式，而大气压氮气均匀放电则是呈现汤森放电模式.大连理工大学的王德真小组［6］研究了电压幅值、驱动频率、放电间距以及二次电子发射系数等控制参量对大气压氦气辉光放电的影响；清华大学的王新新小组［7］也对氦气放电中的多脉冲放电现象进行了研究；Deng等人［8］分别测量了氦气和氮气中能够获得稳定大气压介质阻挡放电的频率范围.然而这些结果大多集中在氦气和氮气这2种气体上，对大气压氩气辉光放电的数值研究相对较少.

本文通过建立一个描述大气压氩气均匀放电的一维等离子体流体模型，数值研究了不同驱动频率下大气压氩气介质阻挡放电的形成机理.模拟发现，当驱动频率较低时，放电为典型的汤森放电模式，随着驱动频率的升高，放电电流不断增大，阴极附近的电场也不断升高，放电逐渐转变为辉光放电模式.

1 模型

选用典型的大气压介质阻挡平板型放电装置，如图1所示.2个距离为d的平行平板金属电极表面分别覆盖有相对介电常数分别为ε1和ε2的电介质，放电区域的厚度为dg，内部充满了纯氩气.位于x＝0处的平板电极上面接有高压交流电源Va（t）＝V0sin，接地平板电极位于x＝d处.由于电极的尺寸远远大于气隙间距，所以可以选用一维的等离子体物理模型.模型中主要考虑电子（e），氩气原子离子（Ar＋）、激发态粒子（Ar＊）以及背景粒子（基态氩原子），考虑的粒子之间的主要反应过程以及反应系数如表1所示.

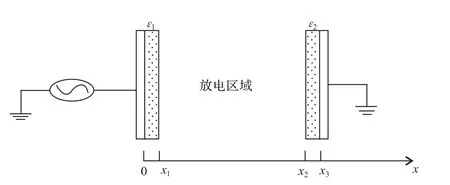
图1 介质阻挡放电结构示意Fig.1 Schematic setup of dielectric barrier discharge

表1 氩气放电基本过程及其反应系数Tab.1 Elementary process of argon discharge and the corresponding reaction coefficients

上述所有的粒子数密度均满足粒子连续性方程

式中，n和Γ分别为粒子数密度和粒子流密度，S为各个反应物粒子的源项.下标e，i以及＊分别代表了电子e、正离子Ar＋以及激发态粒子Ar＊.在漂移扩散近似的条件下，粒子流密度的表达式为

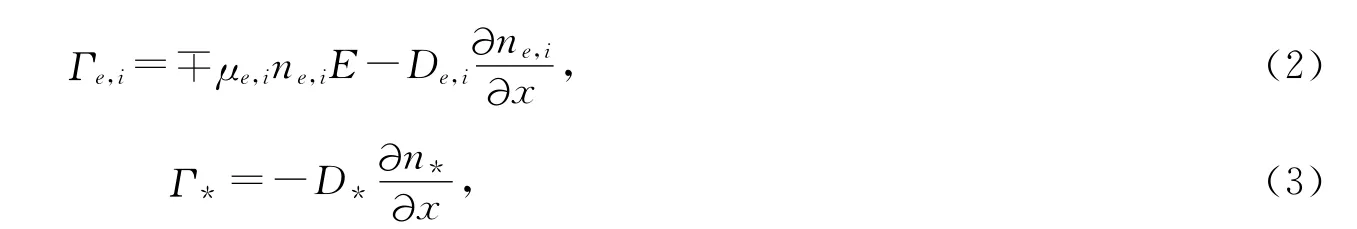
这里D和μ分别为粒子的扩散系数和迁移率，所有粒子的输运系数以及反应系数均来源于文献［9－10］，其中电子直接碰撞电离系数ki（σ）以及亚稳态激发反应系数ke（σ）取决于碰撞截面σ，通过求解玻尔兹曼求解器BOLSIG＋［9］获得.

空间电场E满足泊松方程

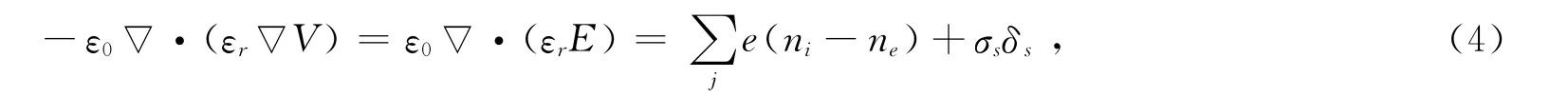
其中V表示电势，e为电子电荷，εr和ε0分别是介质的相对介电常数以及真空介电常数，σsδs表示了沉积在电介质表面的积累电荷密度.

选用的边界条件以及数值算法与文献［6］相同，这里就不再赘述.

2 模拟结果与讨论

模拟计算选取的放电参数如下：电介质厚度均为1mm，相对介电常数为ε1＝ε2＝9，放电间隙宽度dg＝1mm，气压为1.01×105Pa，气体温度Tg＝300K，电子平均温度设置为Te＝2eV，二次电子发射系数γ＝0.1.外加交流电源的幅值为U0＝1 500V，驱动频率为1～100kHz.电子和正离子的初始密度均为空间均匀的恒定值ne＝ni＝107cm－3，而初始亚稳态粒子密度设为n＊＝102cm－3.时间步长在驱动频率小于20kHz下取为10ns，而在大于20kHz的情况下取为1ns.

图2a和b给出了驱动频率为10kHz时的伏安特性曲线以及电流峰值时刻下各种等离子体参量的空间分布情况.在此条件下每半个外加电压周期内只出现1次放电电流脉冲，正负半周内放电情况相同，电流密度峰值大小约为0.6mA／cm2.在整个放电过程中，由于放电过程中产生的带电粒子沉积在介质表面而导致气隙电压Ug稍微有所下降，下降幅值仅为200V左右.通过峰值时刻处电子、离子密度分布以及亚稳态粒子的空间分布，不难看出，此时放电处于典型的汤森放电模式：电子的密度在108cm－3的数量级上，并且在阳极处最高，离子密度在整个放电空间中均比电子密度高，约为1010cm－3，空间电荷形成的电场对外电场的影响不大，所以总电场强度从阳极到阴极几乎呈线性分布.

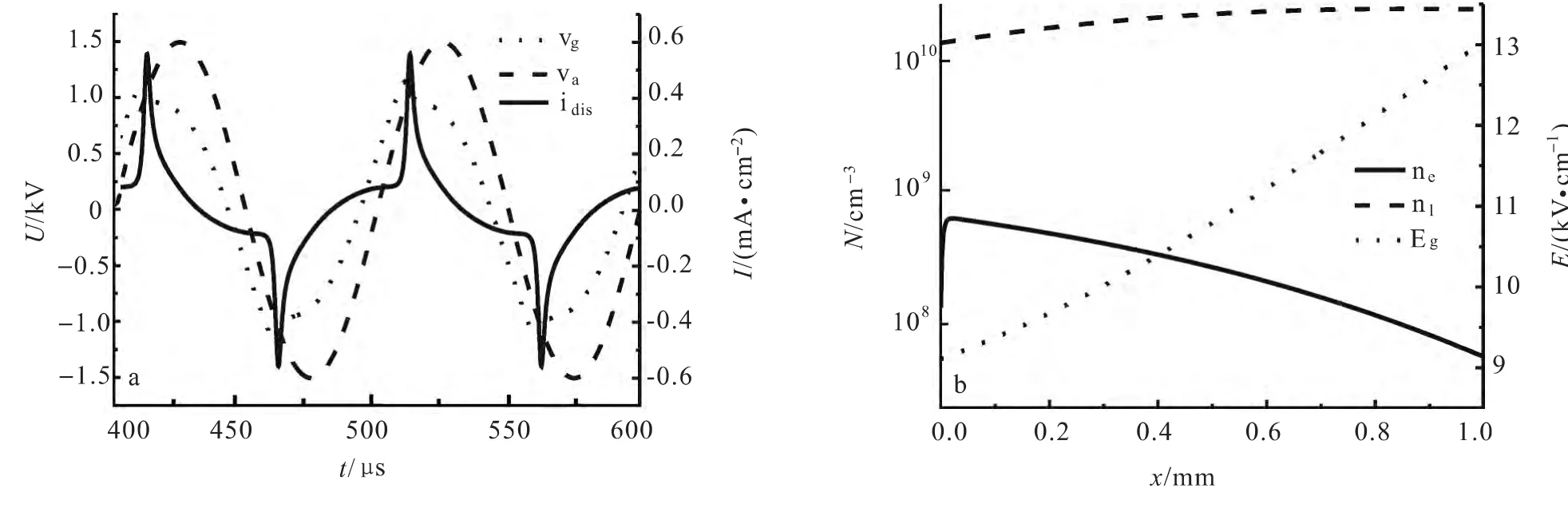
图2 频率为10kHz时的放电波形以及电流峰值时刻等离子体参量的空间分布Fig.2 Waveform of discharge and the spatial distribution of plasma parameters with the frequency 10kHz

模拟结果发现，随着驱动频率的增加，放电模式可以从汤森放电逐步转变为辉光放电.图3给出了驱动频率为50kHz时的放电电流波形图以及相应的带电粒子和空间电场的空间分布图，此时放电电流的峰值大小提高到15mA／cm2，每半个周期内依然只有1个放电脉冲，每个放电脉冲的持续时间比10kHz驱动时要短，且气隙电压在放电过程中的变化较剧烈，约为850V左右.从图3b中可知，在放电电流峰值时刻下放电空间内带电粒子的分布与汤森放电情况明显不同，具有辉光放电的特点：放电区域存在明显的阴极位降区，在此区域内电子的密度高达1010cm－3，且在阴极附近呈指数分布，这是由于此区域的电场强度比较强，放电剧烈，电离程度较高，因而电子密度也比较高.而在阴极鞘层内，由于阴极的排斥作用使得此处的电子密度迅速降低.

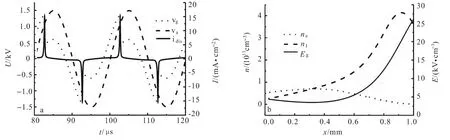
图3 频率为50kHz时的放电波形以及电流峰值时刻等离子体参量的空间分布Fig.3 Waveform of discharge and the spatial distribution of plasma parameters with the frequency 50kHz.

图4给出了放电电流峰值以及放电前后气隙电压的位降ΔU随驱动频率的变化曲线图.随着驱动频率的增加，放电电流和气隙电压变量不断增大，且变化过程基本相同.当频率大于70kHz后，放电在前后2个半周期内情况不同，系统进入非对称放电模式.造成这种变化的原因在于：首先，电压的增长率随着频率增加而增大，克服了表面积累电荷的抑制作用，增强了放电；其次，当驱动频率增加时，2次放电之间的时间间隔减小，上次放电产生的电子剩余的较多，另外，大量剩余的亚稳态粒子也为下次放电提供了更多的种子电子.种子电子的增加造成了放电过程中电子雪崩个数的增加，从而进一步使得放电电流增加，放电电流的此种增加机制也可以通过增大阴极表面的二次电子发射系数来实现.图5给出了不同二次电子发射系数下的放电电流波形图，频率20kHz，电压幅值为2 000V.从图中可以看出，二次电子系数越大，阴极表面由于正离子轰击产生的种子电子越多，因此放电电流也就越大.

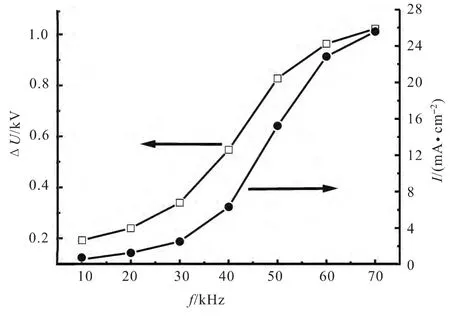
图4 放电电流峰值以及放电过程中气体电压的位降随驱动频率的变化曲线Fig.4 Variation of discharge current peak and the voltage drop as the driving frequency increases

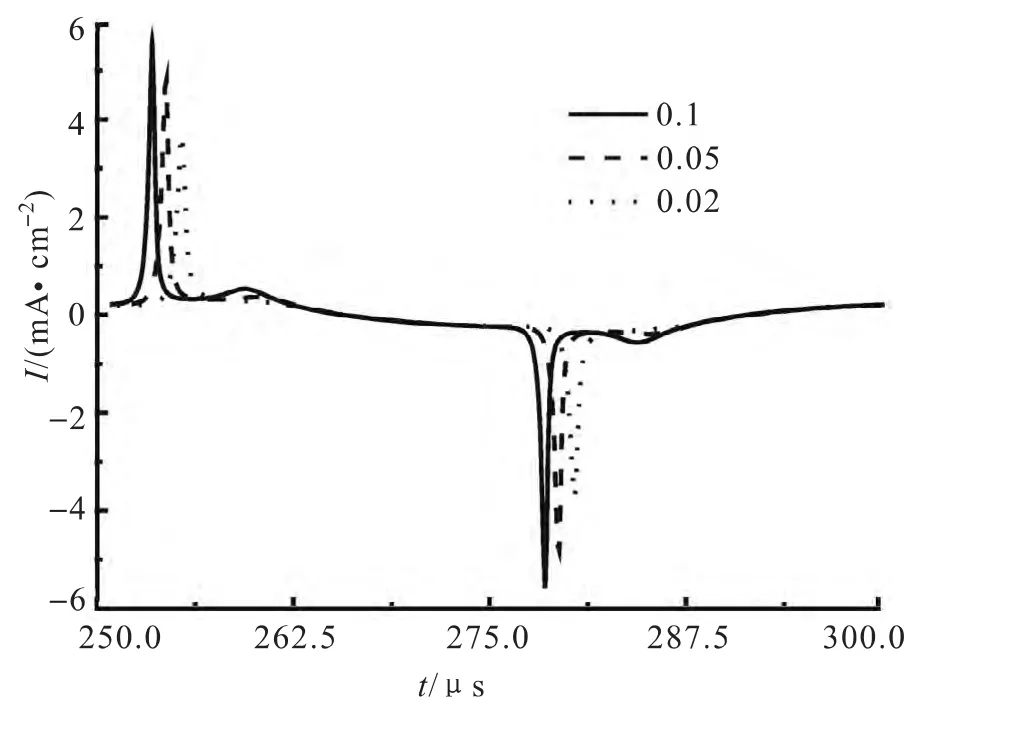
图5 不同二次电子发射系数下的放电电流曲线Fig.5 Discharge current evolution with different secondary electron emission.

3 结论

通过建立一个描述大气压氩气放电动力学的等离子体流体模型，数值模拟了大气压氩气介质阻挡均匀的放电过程.结果表明，在不同的驱动频率下，均匀放电存在着2种不同的放电模式：汤森放电模式和辉光放电模式.当频率较低时，放电电流较小，放电空间内带电粒子密度比较低，放电属于汤森放电；而当驱动频率较高时，放电电流较大，放电进入辉光放电模式.

［1] 郝艳捧，阳林，涂恩来，等.实验研究大气压多脉冲辉光放电的模式和机理［J］.物理学报，2010，59（4）：2610－2615.HAO Yanpeng，YANG Lin，TU Enlai，et al.Experimental study on mode and mechanism of multi－pulse atmosphericpressure glow discharges［J］.Acta Phys Sin，2010，59（4）：2610－2615.

［2] 邵先军，江南，张冠军，等.中频正弦电压下大气压氦气等离子体射流的产生和机理［J］.高电压技术，2012，38（7）：1697－1703.SHAO Xianjun，JIANG Nan，ZHANG Guanjun，et al.Formation mechanism of helium plasma jet at atmospheric pressure under medium－frequency sinusoidal voltage［J］.High Voltage Engineering，2012，38（7）：1697－1703.

［3] MASSINES F，GHERARDI N，NAUDE N，et al.Recent advances in the understanding of homogeneous dielectric barrier discharges［J］.Eur Phys J Appl Phys，2009，47：22805.

［4] ROTH J R，RAHEL J，DAI X，et al.The physics and phenomenology of one atmosphere uniform glow discharge plasma reactors for surface treatment applications［J］.J Phys D：Appl Phys，2005，38：555－567.

［5] 王新新，芦明泽，蒲以康.大气压辉光放电的可能性［J］.物理学报，2002，51（12）：2778－2785.WANG Xinxin，LU Mingze，PU Yikang.Possibility of atmospheric pressure glow discharge in air［J］.Acta Phys Sin，2002，51（12）：2778－2785.

［6] 王艳辉，王德真.介质阻挡均匀大气压辉光放电数值模拟研究［J］.物理学报，2003，52（7）：1694－1700.WANG Yanhui，WANG Dezhen.Numerical simulation of dielectric－barrier－controlled glow discharge at atmospheric pressure［J］.Acta Phys Sin，2003，52（7）：1694－1700.

［7] 吕博，王新新，罗海云，等.大气压氦气介质阻挡辉光放电的数值仿真计算［J］.电工电能新技术，2008，27（3）：63－67.LÜBo，WANG Xinxin，LUO Haiyun，et al.Numerical modeling of dielectric－barrier atmospheric pressure glow discharge in helium［J］.Advanced Technology of Electrical Engineering and Energy，2008，27（3）：63－67.

［8] DENG X T，KONG M G.Frequency range of stable dielectric－barrier discharges in atmospheric He and N2［J］.IEEE Transaction on Plasma Science，2004，32（4）：1709－1715.

［9] HAGELAAR G J，PITCHFORD L C.Solving the Boltzmann equation to obtain electron transport coefficients and rate coefficients for fluid models［J］.Plasma Sources Sci Technol，2005，14：722－733.

［10] BALCON N，HAGELAAR J M，BOEUF J P.Numerical model of an argon atmospheric pressure RF discharge［J］.IEEE Transactions on Plasma Science，2008，36（5）：2782－2787.