加权马尔可夫链在保定地区降雨量预测中的应用

顾志华，商秀印

（河北农业大学理学院，河北保定 071001）

“马尔可夫模型”是俄国数学家Markov在1966年最早提出的，经过几十年不断的发展，Markov过程已成为随机过程的一个重要分支.马尔可夫链可以描绘一个随机变化的动态系统，它根据状态间的转移概率来推测一个系统的未来的发展变化.

降雨过程受气象等条件的影响，存在大量的随机性.如果能够比较准确地预测降雨量，可以为农业等行业的决策提供重要依据.针对保定地区1960—2010年的年降雨量资料，采用均值－标准差分级法，建立了适用于保定地区的年降雨量分级标准.并用加权马尔可夫链对保定地区2011和2012年年降雨量状态进行了预测，考虑到马尔可夫链只能预测出降雨量的某一区间，故本文又结合模糊集理论对2011和2012年的降雨量进行了预测.

1 保定地区年降雨量状态的确定

设降雨量序列为X1，X2，…，Xn，采用均值－标准差分级法，将各年降雨量进行状态分级，分为枯水年、偏枯年、平水年、偏丰年和丰水年5个状态.保定地区1960—2010年降雨量的均值＝522.65，标准差S＝148.46.年降雨量分级见表1，区内1960—2010年降雨量序列及其状态见表2.

表1 年降雨量分级表Tab.1 Annual rainfall classification

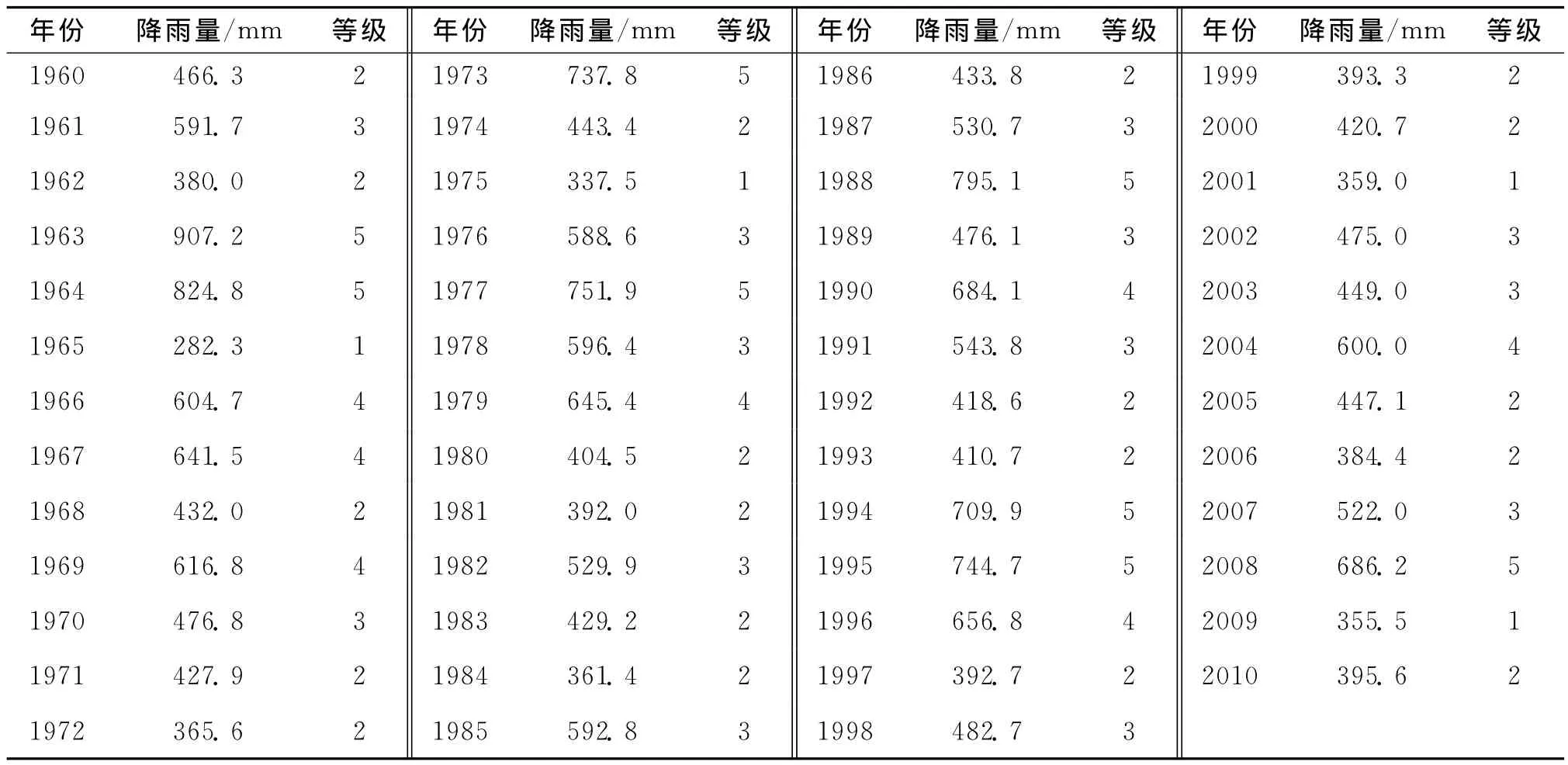
表2 年降雨量序列及其状态Tab.2 Annual precincepition sequence and state

2 加权马尔可夫链预测过程

1）采用均值－标准差分级法，确定状态空间，以此来确定序列中各指标值的状态.

2）符号表示.

fij为研究序列X1，X2，…，Xn中从i状态出发，经过一步转移到达状态j的频率.＝为转移频率矩阵为边缘频率（m为状态值）.

3）对研究序列进行马氏性检验.

4）计算序列各阶自相关系数rk.

式中，Xi为第i时段的指标值—指标值平均值.

5）把各阶自相关系数规范化，即

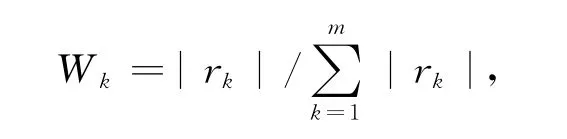
式中，m为预测时需要计算到的最大阶数.

6）分别以前面若干时段的指标值为初始状态，结合其相应的各阶转移概率矩阵，即可预测出该时段指标值的状态，k为滞时（步长）.

7）将同一状态的各预测概率加权和作为指标值处于该状态的预测概率，即所对应的即为该时段指标值的预测状态.

8）对各状态分别赋予相应的权重，即权重集ω＝｛ω1，ω2，ω3，ω4，ω5｝，其中为最大概率的作用系数，这里取2.级别特征值如果年降雨量预测状态为i，且H≥i，则年降雨量的预测值为如果H＜i，则预测值为其中Ti，Bi分别为状态区间值的上限和下限.

3 加权马尔科夫链模型在保定地区降雨量预测中的应用

1）进行马氏检验

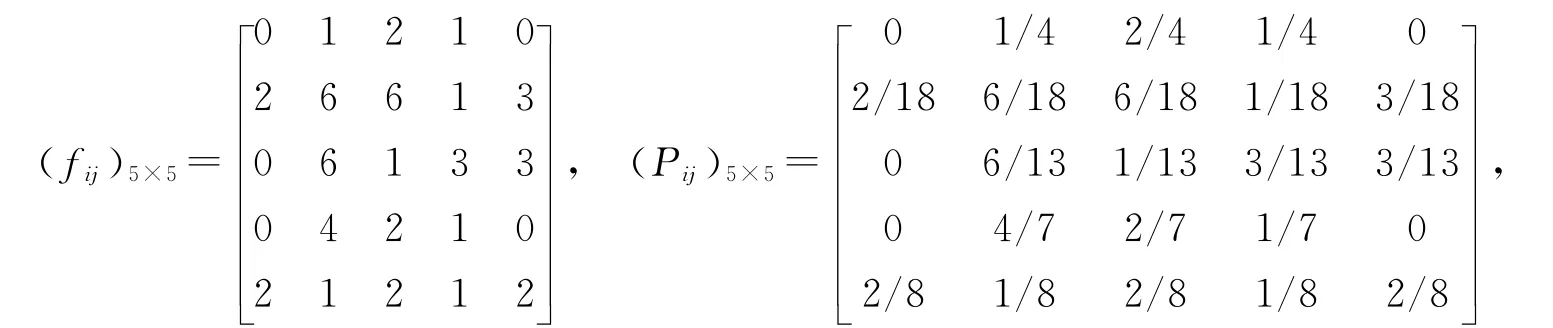
2）各阶自相关系数及权重的计算（表3、表4）

表3 1～5阶自相关系数及权重Tab.3 1～5the self correlation coefficients and the weights

表4 2～6阶自相关系数及权重Tab.4 2～6the self correlation coefficients and the weights

3）根据2004—2008年的年降雨量数据，采用1～5阶权重系数，对2009年的降雨量状态进行预测，结果见表5.

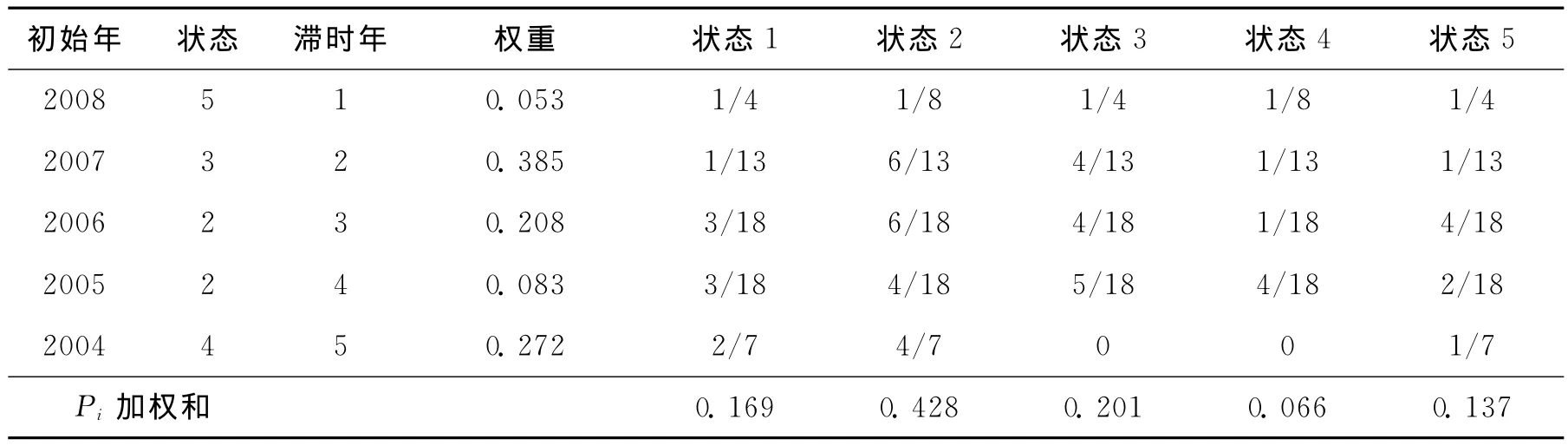
表5 2009年的降雨量状态预测（利用表3）Tab.5 Predication of annual rainfall states in 2009（with tab.3）

由上表知max（P）＝0.428，根据模糊集理论，由公式预测2009年降雨量340.68mm，实际降雨

i量为355.50mm，相对误差为4%.

根据2003—2007年的年降雨量数据，采用2～6阶权重系数，对2009年的降雨量状态进行预测，结果见表6.

表6 2009年的降雨量状态预测（利用表4）Tab.6 Predication of annual rainfall states in 2009（with tab.4）

由上表知max（Pi）＝0.353，此时i＝2，即2009年年降雨量预测状态为2，而2009年年降雨量实际状态也为2，和预测状态相吻合.根据模糊集理论，由公式预测2009年降雨量为371.88mm，实际降雨量为355.50mm，相对误差为4%.

根据2005—2009年的年降雨量数据，采用1～5阶权重系数，对2010年的降雨量状态进行预测，结果见表7.

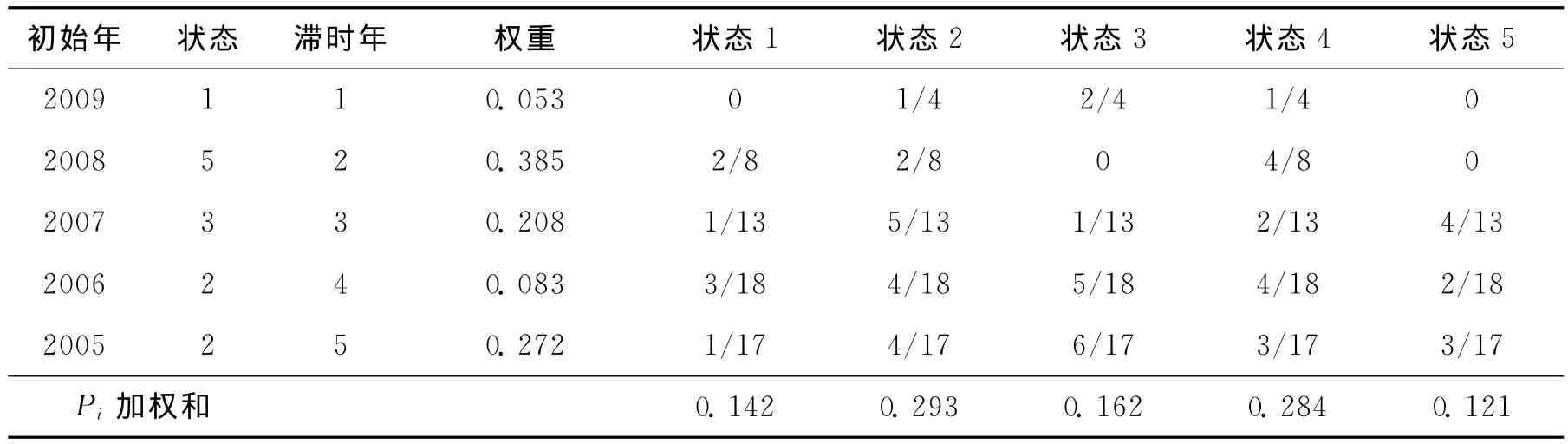
表7 2010年的降雨量状态预测（利用表3）Tab.7 Predication of annual rainfall states in 2010（with tab.3）

由上表知max（Pi）＝0.293，此时i＝2，即2010年年降雨量预测状态为2，而2010年年降雨量实际状态也为2，和预测状态相吻合.根据模糊集理论，由公式预测2010年降雨量为437.78mm，实际降雨量为395.00mm，相对误差为10%.

根据2004—2008年的年降雨量数据，采用2～6阶权重系数，对2010年的降雨量状态进行预测，结果见表8.

由上表知max（Pi）＝0.276，此时i＝2，即2010年年降雨量预测状态为2，而2010年年降雨量实际状态也为2，和预测状态相吻合.根据模糊集理论，由公式预测2010年降雨量为424.85mm，实际降雨量为395.00mm，相对误差为7%.

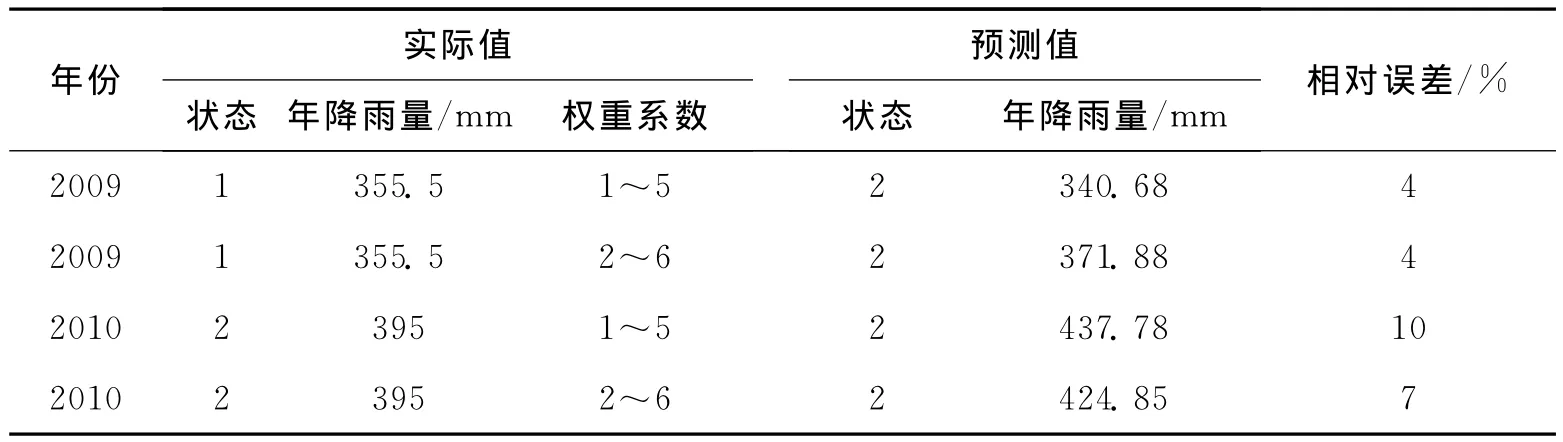
表9 实际与预测结果Tab.9 Actual and predictive results

4 结论

无论是1～5阶权重还是2～6阶权重来预测降雨量，误差控制在10%以内，因此更加说明了加权马尔可夫链预测模型的可靠度.重复以上方法，即根据1960—2010年年降雨量序列，以2006—2010年作为初始年，用1～5阶权重系数预测出2011年年降雨量为468.77mm，用2～6阶权重系数预测出2012年的降雨量为618.51mm.

［1] 王涛，钱会，李赔月.加权马尔可夫链银川地区降雨量预测中的应用［J］.南水北调与水利科技，2010，1（8）：78－81.WANG Tao，QIAN Hui，LI Peiyue.Prediction of precipitation based on the weighted Markov chain in Yinchuan area［J］.South－to－North Water Transfers and Water Science Technology，2010，1（8）：78－81.

［2] 谢波涛.台风飓风影响海区固定式平台设计标准及服役期安全度风险分析［D］.青岛：中国海洋大学，2010.XIE Botao.The analysis of the design criterion and dynamic reliability assessment of existing platform in Typhoon／hurricane affected region［D］.Qingdao：Ocean University of China，2010.

［3] 夏乐天.马尔可夫链预测方法及其在水文序列中的应用研究［D］.南京：河海大学，2005.XIA Letian.Research of Markov chain prediction method and its application on Hydrology series［D］.Nanjing：Hohai U－niversity，2005.

［4] 仲远见，李靖，王龙.改进马尔可夫链降雨量预测模型的应用［J］.济南大学学报：自然科学版，2009，23（4）：402－405.ZHONG Yuanjian，LI Jing，WANG Long.Precipitation predicting model based on improved Markov chain［J］.Journal of University of Jinan：Science Technology，2009，23（4）：402－405.

［5] 姜昊.灰色马尔可夫预测模型在台风诱发灾害研究中的应用［D］.青岛：中国海洋大学，2009.JIANG Hao.The Application of Grey－Markov forecasting model in the research of Typhoon induced disasters［D］.Qingdao：Ocean University of China，2009.

［6] 李娟，张维江，马轶.滑动－平均马尔可夫模型在降水预测中的应用［J］.水土保持研究，2005，12（6）：196－198.LI Juan，ZHANG Weijiang，MA Yi.Application of moving Average－Markov chain in the prediction of precipitation［J］.Research of Soil and Water Conservation，2005，12（6）：196－198.

［7] 孙才志，林学钰.降水预测的模糊权马尔可夫模型及应用［J］.系统工程学报，2003，18（4）：295－298.SUN Caizhi，LIN Xueyu.Research on fuzzy Markov chain model with weights and its application in predicting the precipitation state［J］.Journal of Systems Engineering，2003，18（4）：295－298.

［8] 童精勤.年降雨量的预测研究［J］.武汉理工大学学报，2008，30（7）：99－102.TONG Jingqin.Research of predicting the precipitation in one year［J］.Journal of Wuhan University of Technology，2008，30（7）：99－102.

［9] 冯耀龙，韩文秀.权马尔可夫链在河流丰枯状况预测中的应用［J］.系统工程理论与实践，1999（10）：89－98.FENG Yaolong，HAN Wenxiu.The application of weighted Markov－Chain to the prediction of River Runoff State［J］.Systems Engineering－Theory ＆Practice，1999（10）：89－98.