基于Java BigInteger类的大整数运算应用
2014-10-08申时全SHENShiquan
申时全 SHEN Shi-quan
(广东科技学院,广州 510635)
(Guangdong University of Science&Technology,Guangzhou 510635,China)
0 引言
Java提供了进行大整数计算的类BigInteger,封装了大整数的加(add)、减(subtract)、乘(multiply)、除(divide)以及求余(remainder)运算,还封装了大整数的幂运算(power)和比较(compare)运算等。通过使用这些大整数运算,可以求解许多高精度运算问题。
计算具有100位以上精度的黄金分割系数、计算100位以上精度的圆周率、计算具有100位以上十进制数的大整数都是具有重要意义的事。应用Java的BigInteger类,可以方便地解决这些问题。
1 Java BigInteger类封装
Java的BigInteger类是java.math包中的一个类,提供任意精度的整数运算。
1.1 构造大整数对象 Java中的大整数是BigInteger类的对象,构造大整数对象的构造方法是:
public BigInteger(String val)
因此,为构造一个大整数对象需要用该构造方法,步骤是:申明对象bignum,用new操作创建该对象。例如构造一个20位数9999999999999999999,可用如下语句实现:
BigIntegerbignum=new BigInteger(“99999999999999 99999”);
然后可通过对象bignum调用相关计算方法。
1.2 BigInteger类封装的主要方法 BigInteger类封装了以下常用方法,实现另一个大整数对象与本对象的运算,并生成一个新的大整数对象(比较运算除外)。另外,还封装了与大素数的方法,这些方法是:
①获取一个给定位数和随机数位的大素数,是一个静态(static)方法,定义如下:
public static BigInteger probablePrime(int bitLength,Random rnd):该方法获得一个可能性很的具有二进制bitLength位的大素数,其概率为1-2-100。
②获取下一个可能素数的方法,方法定义如下:
BigInteger nextProbablePrime();该方法返回一个与当前的可能素数p,最接近的可能素数q;对于任意p ③将一个长整型转换为BigInteger对象的方法,方法定义如下: public static BigInteger valueOf(long val);该方法返回长整型数val的bigInteger对象。 ④判断大整数是否为可能素数的方法,方法定义如下: boolean isProbablePrime(int certainty);若对象num.isProbablePrime(cer)返回true,则num是素数的概率大于1-2-cer。 ⑤求余数运算方法remainder(),方法定义如下: public BigInteger remainder(BigInteger opnd);实现一个大整数对象与另一大整数对象opnd的求余运算,并返回余数(一个大整数对象)。 ⑥求大整数的商和余数的方法 divideAndRemainder(BigInteger opnd),该方法返回大整数对象除以大整数opnd的商和余数,用一个BigInteger类型数组存放,例如: BigInteger aBig[]=new BigInteger[2]; BigInteger num=new BigInteger(“125”); aBig=divideAndRemainder(num,new BigInteger(“23”)); 那么aBig[0]是125除以23的商5,aBig[1]是余数10。 其余方法这里就不多加叙述,可参考文献[1]。 可应用BigInteger类进行高精度计算问题的求解,方法简便。求解步骤如图1。 图1 3.1 高精度黄金分割系数问题的求解 黄金分割系数0.61803...是个无理数,这个常数十分重要,在许多工程问题中会出现。有时需要把这个数字求得很精确。比较简单的一种是用连分数表示,如图2。 图2 这个连分数计算的“层数”越多,它的值越接近黄金分割数。 我们需要求出黄金分割数的足够精确值,四舍五入到小数点后100位。 我们可以将黄金数的计算抽象为以下表达形式: 可以将上式转换为分数形式:nk/dk,那么,nk+1=dk,dk+1=dk+nk,n0=1,d0=1。 由此递推,计算分子和分母,直到分子≥10100,这样,可保证结果满足能得到所要求精度。然后是将分子乘上10100,在与分母做除法,得到的就是100位的大整数,就是这个黄金数的小数点后的数字,经四舍五入处理并转换成字符串输出即可,通过对余数的判断,可确定是否要在结果中加1。程序如下: 3.2 求大素数问题的程序 大素数是数据加密与解密问题的核心,在RSA加密体系中,为了生成RSA算法的公钥和私钥的秘钥对,先要选择两个大素数p和q,并计算它们的乘积N。我们这里用Java的BigInteger类来产生具有100位(当然可以更多,视需要而定)十进制数的大素数。对于大素数的判断,并没有一个严密的数学公式可供应用。可用BigInteger类中相关运算方法,结合素数相关方法,可以求出给定位数(二进制)的可能大素数,且具有随机性。 可以用BigInteger类的probablePrime()方法生成给定位数的近似大素数(称为概素数),其准确度可用一个参数进行控制。下面的程序生成若干个随机生成的具有330位二进制位(具有100位十进制)的大素数。BigInteger.probablePrime(bitNum,rnd)生成的“概素数”具有bitNum位二进制,其是素数的概率大于1-2-100。为了提高可靠性,程序中对生成的“概素数”进行更严格测试,用10000做参数,用isProbablePrime(10000)测试,该方法保证素数的概率大于1-2-10000。 3.3 求解与梅森素数有关的问题 根据法国数学家梅森的猜想,我们习惯上把形如:2n-1的素数称为:梅森素数。截止2013年2月,一共只找到了48个梅森素数。新近找到的梅森素数太大,以至于难于用一般的编程思路验证。这里要解决的是跟梅森素数有关的一个问题:1963年,美国伊利诺伊大学为了纪念他们找到的第23个梅森素数n=11213,在每个寄出的信封上都印上了“211213-1是素数”的字样。211213-1这个数字已经很大 (有3000多位),编程求出这个素数的十进制表示的最后100位。直接用BigInteger类求解该问题相关语句如下: 本文介绍了Java中的BigInteger类的一些典型应用。BigInteger类中包装了绝大多数大整数运算功能,文中没有完全涉及,可参考Java有关技术资料,应用Java的BigInteger类求解一些高精度运算问题,十分方便。特别说明的是,符合费尔马定理的大整数只符合素数的必要条件,但不是充分条件。本文中所给程序计算的结果,只能是有极大可能性是素数,其可能性超过1-2-10000。如果要用所有小于待测“概素数”的平方根的所有概素数去检测一个数百位十进制位需要很长时间,并不实用。 [1]耿祥义,张跃平.Java面向对象程序设计(第2版)[M].北京:清华大学出版社,2013. [2]王英.RSA算法中安全大素数的选择[J].西安:西安工业学院学报,2005. [3]Mark Stamp,Information Security:Principles and Practice[M].by Wiley Publishing,Inc,2011(张戈译,信息安全原理与实践(第 2版)[M].北京:清华大学出版社,2013).2 BigInteger类在高精度计算问题中的应用
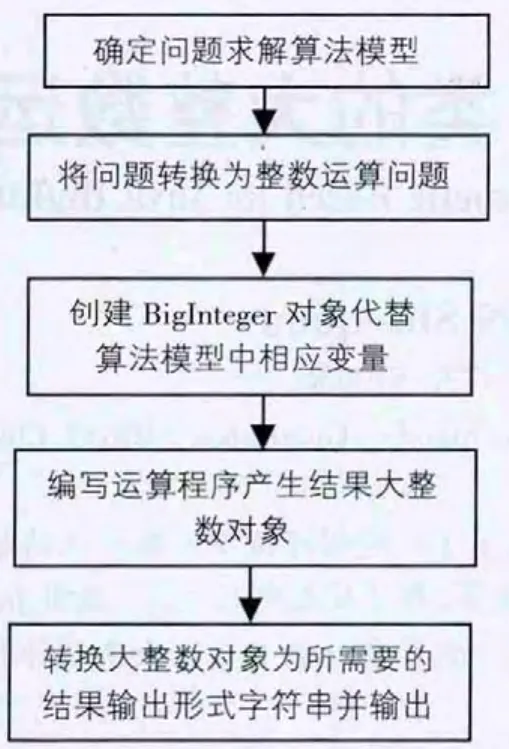
3 典型问题的大整数求解

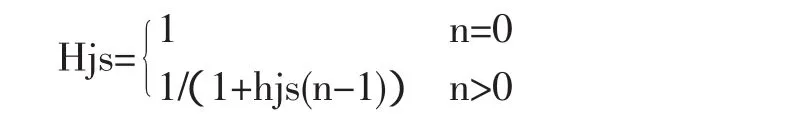




4 结束语
