基于模块化多电平的海上风力发电系统的研究
2014-10-08陈明彩CHENMingcai
陈明彩 CHEN Ming-cai
(山东科技职业学院,潍坊 261053)
(Shandong Vocational College of Science&Technology,Weifang 261053,China)
0 引言
在我国陆地和海上风能资源十分丰富。同陆地风力资源相比,海上风电具有风速高,范围广,涡流强度较小等优点。所以,我国把大力发展海上风力发电项目作为未来风力发电的重点。但是,由于海上风力发电场一般都距离陆地较远,再加上风能具有间歇性和不可控性,所以如何把海上风电高效、安全可靠的送到负荷中心是我们需要重点研究的一个课题[1]。
基于此,本文采用了一种十分适合海上轻型直流输电的拓扑结构—模块化多电平变换器。MMC是由德国西门子公司于2002年提出的一种新型的多电平拓扑结构并成功应用在高压直流输电领域,MMC输出电压高、谐波畸变小,模块化结构具有较强的故障容错能力,并且即可实现AC/DC整流变换,也可实现DC/AC逆变变换。MMCHVDC技术作为目前国际上高压直流输电领域的研究热点。研究基于海上风力发电的MMC-HVDC输电技术具有十分重要的现实意义。
将MMC应用在高压直流输电领域,需要重点解决两个问题:有功功率和无功功率解耦控制[2]和MMC子模块电容电压平衡控制。本文提出了一种新型的功率解耦控制策略和电容电压均衡控制算法。
1 MMC-HVDC拓扑结构
如图1所示为海上风力发电场与电网相连接的MMC-HVDC系统结构图。图中的两个换流站均采用MMC拓扑结构,风力发出的三相交流电首先通过MMC1整流变换,然后通过长距离输电电缆传输到逆变换流站MMC2,MMC2输出三相交流电并到电网。为了简化模型,本文将风电场的输出等效为理想电压源。
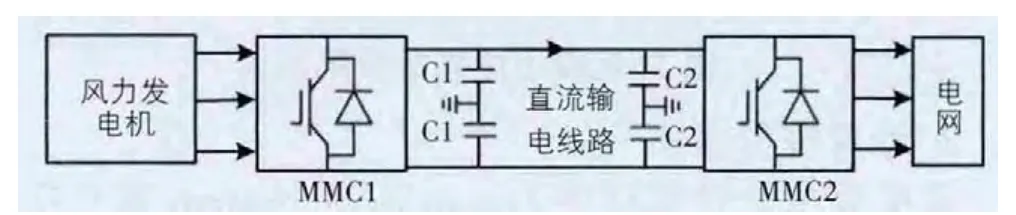
图1 MMC-HVDC主拓扑结构
2 MMC数学模型
如图2所示为MMC拓扑结构,MMC有6个桥臂构成,其中每个桥臂有若干个相互连接且结构相同的子模块(sub module,SM)与一个电抗器串联构成,上下两个桥臂构成一个相单元。6个桥臂具有对称性,各子模块的电气参数和桥臂电抗值都是相同的。
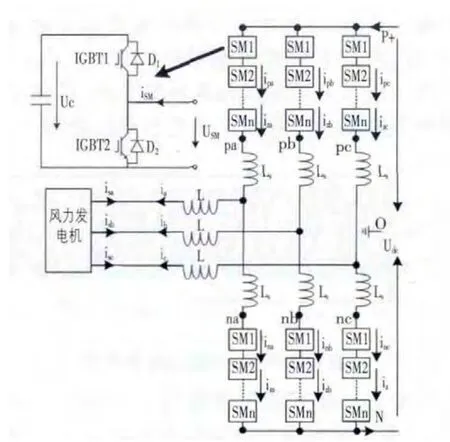
图2 MMC电路拓扑结构
为了保证直流侧母线电压的恒定,对于任意一相任意时刻必须保证投入的模块数相同且等于n,即上桥臂投入一个模块,下桥臂必须切除一个模块或者上桥臂切除一个模块,下桥臂投入一个模块,否则会引起相间环流和相内模块电容电压大幅度波动[3]。
由MMC拓扑结构可知,在任意时刻,直流侧电压Udc由各相上、下桥臂中处于输出状态的子模块和两电抗器LS共同承担。即满足:

上式中,Udc为直流侧母线电压,ipx和inx分别是第x相上、下桥臂电流。其中x=a,b,c。理论上,MMC中每相处于输出状态的子模块个数恒定不变且个数为该相子模块数目的一半,即为n。若Mx设为x相上桥臂中处于输出状态的子模块数,Px相下桥臂中处于输出状态的子模块数,则满足:

正常运行过程中,MMC三相之间能量分配的不均匀将会产生相间环流,设流过第x相的环流为izx,方向如图所示。由于MMC结构的严格对称,可视为能量在上下桥臂均分,所以可以得出如下方程式[4]:

上式为MMC输出电压的动态数学模型,通过控制上、下桥臂的子模块的投入状态来输出所需要的三相交流电压。当变流器稳态运行时,忽略直流电压的波动和限流电感上的压降,由其引起的误差通过控制系统闭环环节加以校正。
3 功率传输控制
本文采用电压电流双闭环控制方式控制风场和电网侧变流器协调运行。要想实现功率的传输控制,需要建立数学模型设法对有功功率和无功功率进行分别控制。本文采用的电压电流双闭环控制中电压外环和电流内环调节均采用PI调节。电压外环调节器的输出为内环有功电流(d轴)和无功电流(q轴)的参考值。为了使d轴和q轴迅速跟踪外环电压调节器输出,内环采用前馈解耦控制,控制框图如图3所示。
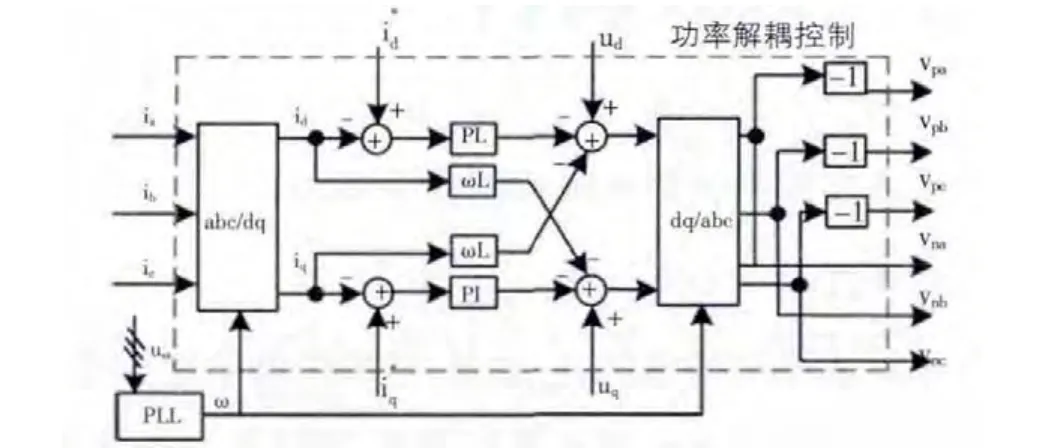
图3 功率解耦控制框图
由图3可列出如下KVL方程:

上式中,ud、uq分别为风力发电机相电压在d-q旋转坐标系下的d-q分量,udo、uqo分别为MMC交流输出端相电压在d-q旋转坐标系下的d-q分量,id、iq分别是MMC交流侧三相电流在d-q旋转坐标系下的d-q分量,ω为电网电压角频率,是通过PLL锁相环对电网电压锁相得到的。再通过解耦控制最终可以得到以下控制方程:

4 电容电压平衡控制
如何保障MMC各悬浮、独立的直流电容电压的稳定是其正常工作的基本要求。为了实现MMC各子模块电容电压的稳定控制,本文提出了一种新型的电容电压平衡控制算法。该算法可以分为两部分:能量均分控制和电压均衡控制。
4.1 能量均分控制 能量均分控制就是使各子模块电容电压的平均值跟踪它的参考值,从而控制MMC相间环流的大小使能量均匀的分配到各子模块中。如图4为能量均分控制的控制框图。

图4 能量均分控制框图
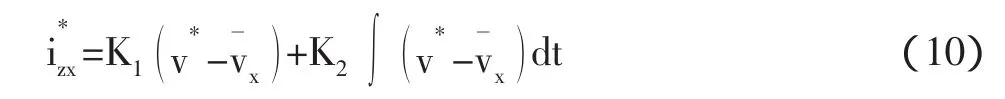
平均控制得到的电压调制参考值为:
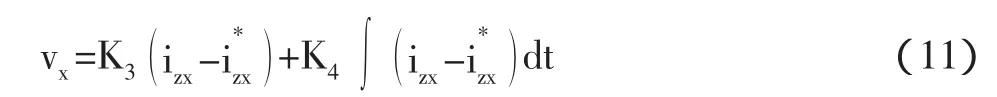
当v*大于平均值时上升,结果影响电流内环,迫使izx跟踪。最终目标是为通过控制izx使得子模块平均值跟踪其参考值v*而不受交流侧电流的影响。
4.2 电压均衡控制 电压均衡控制的目的就是使MMC各子模块电容电压跟踪其参考值,其控制框图如图5所示。对于x相上、下桥臂子模块的电压控制修正量为如下表达式[13]:

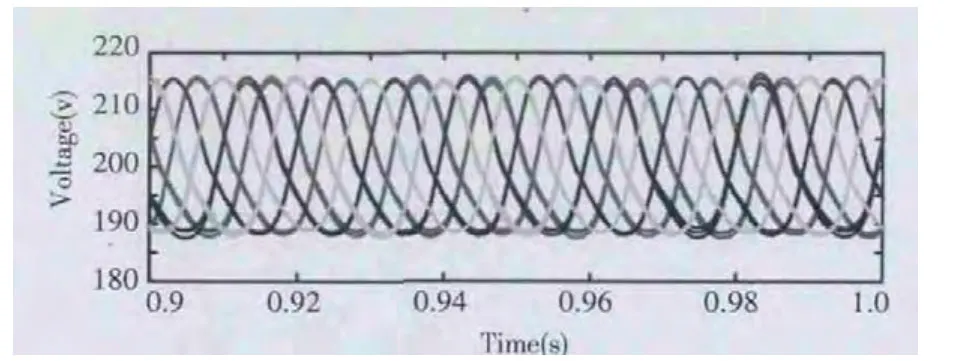
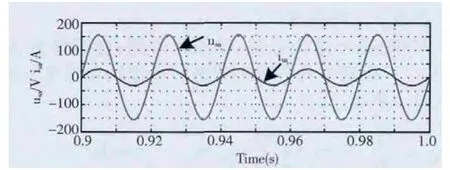
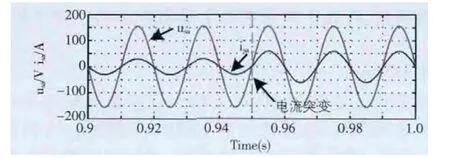
当参考电压的值v*大于等于电容电压upxi(unxi)的值时,由于upxi(unxi)值为正,为了使子模块中的电容电压迅速接近参考电压,子模块需要从直流侧吸收电能。如果电流值ipx(inx)为正值,这时得到的电容电压修正量Δvpxi(Δvnxi)为正,这时就会控制开关器件来改变子模块的状态,使电容的充电时间延长;当电流值ipx(inx)为负时,这时得到的电容电压修正量Δvpxi(Δvnxi)为负。此时就会对开关器件进行相应控制,减小电容放电时间。当v* 图5 电压均衡控制框图 在MATLAB/SIMULINK中搭建MMC-STATCOM仿真模型,MMC每相带6个子模块,上、下桥臂各3个,限流电抗器Ls=2mH,模块电容C=5000uf,电容电压参考值设定为200V,滤波电感L=1mH.电网相电压为110V,载波频率为5kH。 图6为MMC采取电容电压平衡控制后所有子模块的电容电压波形,从图中可以看出所有的电容电压维持在200V左右,且上下桥臂的波形趋势相反,这是由于上、下桥臂子模块投入和切除状态互补造成的。证明了上述电容电压控制策略能够很好的维持电容电压平衡。 图6 MMC子模块电容电压 风力发电一般期望只传输用功功率,不传送无功功率,所以仿真中设定风力发电机发出的无功电流参考值为零。仿真结果如图7所示,从图中可以看出风力发电机输出电压与输出电流同相位,实现了单位功率因数传输电能,验证了前面提出的解耦控制算法的有效性。 图7 风力发电机相电压和相电流 风力发电机电流由突然变化时,MMC A相电流的变换曲线如图8所示。从图8中可以看出,MMC可以迅速跟踪上电流变化并达到稳定,具有较快的动态响应速度。 图8 电流突变情况下风力发电机相电压和相电流 本文首先分析了基于海上风力发电的MMC-HVDC的基本工作原理MMC的数学模型;然后提出了有功和无功功率解耦控制算法和MMC子模块电容电压平衡控制策略;最后通过matlab仿真实验验证了所提出的控制策略的有效性和正确性。 [1]李响,王志新,刘文晋.海上风电柔性直流输电变流器的研究与开发[J].电力自动化设备,2009,29(2):10. [2]傅晓帆,周克亮,程明等.风电场并网用VSC-HVDC的无差拍解耦控制策略[J].电工技术学报,2009,24(11):157-164. [3]M.Hagiwara and H.Akagi,"Control and Experiment of Pulsewidth-Modulated Modular Multilevel Converters,"IEEE Trans.Power Electron.,2009,24(7):1737-1746. [4]H.Akagi,“Classification,terminology,and application of the modular multilevel cascade converter(MMCC),”IEEE Trans.Power Electron.,2011,26(11):3119-3130. [5]陈潼,赵荣祥.并网逆变器间接电流解耦控制策略的研究[M].电力电子技术,2006.
5 仿真与实验结果分析
6 结语
