基于径向基函数神经网络的海南省社会经济数据分析

吴 慰，杜文才

(海南大学信息科学技术学院，海南海口570228)

经济增长质量的研究具有深远的理论价值和重要的实践意义.随着社会发展的日趋完备，数据的统计分类更加详细，数据量也大大增加.一方面，这些数据能为小门类和整体分析提供很好的参考和依据，但是从另一方面讲，这些日益增加的大量数据也给我们分析和提炼重点数据带来了新的问题.

目前，常用的经济增长质量的评价方法大多是从经济决策变量方面来分析.综合评价是从经济、社会等方面来构建经济增长质量的综合模型，它能反映高维矩阵数据的真实性和准确性，然而，无论是古典的经济增长理论还是新经济理论，它们均受模型中变量的影响.在数据预测方法中，采用重要的决策变量或者是使用回归分析的方法来分析整体数据，虽然能够获得较好的结果，但是，所引入的分析常使得问题的复杂度大大提高，而且还存在着以局部问题的求解代替全面解的现象，仍然存在着分析不准确的情况.此外，采用高维的函数进行拟合不仅剔除了一些真实存在的却在分析中看似异常的数据点，而且高维的数据还使得运算与纠错性成为了瓶颈，这也就使得全局分析方法的提出成为了必然.

1 基础知识

1.1 数据模型 函数模型的确立首先需要解释变量与被解释变量.就经济数据而言，往往是以被广泛关注的国内生产总值(Gross Domestic Product)和居民消费价格指数(Consumer Price Index)等作为重要的评价指标，而将历年的能源与消费情况等等因素均视为与其有正相关作用的解释变量.

假设单一评价指标目标函数与决策变量之间存在如下相关关系:

其中xi表示解释变量，fe表示评价指标.在一个评价指标不能准确反映实际需求时，可以以被解释变量来构建矩阵决策关系，同时，考虑到初始状态的数值赋值问题，可以以一个相同维度的初始矩阵C作为偏置.

在此处，该矩阵不同列的元素之间是相互独立的，每一个列表示一种属性的变量.可以证明，该矩阵是满秩的，完成数据采集后，该矩阵就是一个反映指标体系的和满足能控性与能观性的矩阵.

在经济学中，无论采用空间权值矩阵中的基于邻接概念的空间权值矩阵(Contiguity Based Spatial Weights)还是采用空间权值矩阵中的基于距离的空间权值矩阵(Distance Based Spatial Weights)来描述变量的依赖关系，都存在极强的元素间的耦合关系，因此提出，应采用神经网络权值的训练方法来实现指标分析.

1.2 径向基函数神经网络 现代的计算机具有很强的计算和信息处理能力，但是，它在模式识别、感知和于复杂的环境中做出决策等问题中却远不如人［1］.因此，人们从模仿人脑智能出发，赋予计算机人工智能的优势，并将它应用于社会生活的各个领域，这就是人们对于人工神经网络(Artificial Neural Networks)的研究所在［2－3］.神经网络是由具有适应性的数据运算单元组成的互联网络，它模拟生物学中生物的神经系统对真实环境做出的交互反应［4］.人工智能神经网络是由大量并行分布的简单神经元构成，信号则是在各层神经元之间传递.

径向基函数神经网络(Radial Basis Function Neural Networks)在结构上有很多优点，如非线性化结构与参数、大量并行分布式结构、克服局部极小值、自我学习与适应能力等，这使得它的应用不断的扩大.

神经元的最基本形式如图1，它构成了神经网络的层次结构，神经网络的每一层发挥着不同的作用;输入层由一些源点组成，第二层是隐含层，它将感知器从外界获取的数据于隐含层之间进行非线性变换;输出层基于激活函数，它对偏置信号和输入数据做出规范化响应并输出;隐藏空间的维数越高，逼近就越精确［5］.

图1 径向基函数神经网络的神经元结构

隐含层神经元训练实质上是通过不断地调整权值来实现的.RBFNN的形式可以表示为［6］:

其中，神经网络的输入向量是一个有界紧集，W=［w1，w2，…，wm］TRm是权值向量，m是网络的中心节点数目，si(x)是径向基函数，应用最为广泛的是高斯基函数，其形式如下:

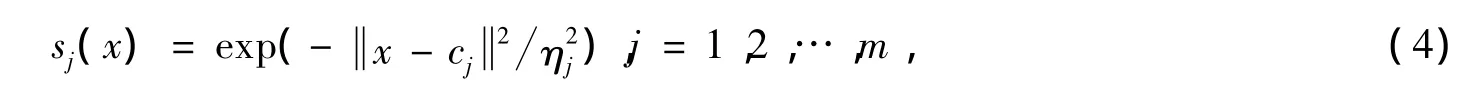
其中，cjΩx，j=1，2，…，m是中心节点，它决定中心结点对应的基函数的作用范围.当中心结点数足够多，而且分布合理时，神经网络在有界紧集Ωx内能够逼近连续函数h(x)，且逼近误差可以达到任意小［7-8］.隐含层神经元训练实质上是通过不断地调整权值来实现的.神经网络训练过程结束后，在将任意输入向量送给该神经网络时，RBFNN中的每个神经元都将根据输入向量接近每个神经元权值向量的程度来输出结果.这个过程运行的结果是:与输入向量相离很远的权值向量，其对应的神经元的输出接近0，这些很小的输出对后面的线性层的影响可以忽略;而与输入向量非常接近的权值向量，其对应的神经元的输出接近1.

设隐含层共有m个神经元，当隐含层神经元的权值wj确定后，由图2可知，神经网络的输出为:

其中，b为偏置.本文中神经网络网的学习是有导师训练规则的，它是用历年的决策变量数据和目标矩阵函数作为导师指导规则来进行训练;因此，可利用各种线性优化算法来求得各神经元的连接权系数.

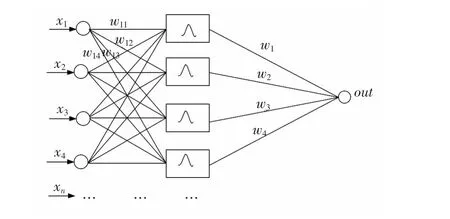
图2 3层神经网络的学习机制实例

2 数据准备

从经济增长的大指标出发，笔者选择了如下的几类统计数据作为决策相关因子，并予以分析，见表1.

表1 海南省2001—2012年部分经济数据统计表*

3 模型的建立与分析

3.1 模型建立 根据表1的数据，使用MATLAB神经网络对2001—2010年的数据进行训练，即选择以下几类数据进行分析:全社会存款余额x1(单位:亿元，下同)，x1反映了人们工资或积蓄情况;就业人数(万人)x2，它反映企业与社会的状况;财政总收入x3，它在一定程度上反映了公共事业的健康与否;社会消费品零售总额x4，它反映了人们的消费情况;全社会固定资产投资x5，它反映了对未来预期的判断情况.以上这几类数据均作为样本决策变量，而Gdp与能源消耗总量Eng则作为检测与预测指标.将c设置为零矩阵，可以得到:其中，xij表示解释变量，fei表示评价指标.于此处，该矩阵不同列的元素之间是相互独立的，每一个列表示一种属性的变量.可以证明，该矩阵是满秩的，完成数据采集后该矩阵是一个反映指标体系的和满足能控性和能观性的矩阵.

3.2 预测分析 在MATLAB中编写预测函数与数据.

可以得到的训练学习收敛过程如图3所示，图4给出了学习训练过程及误差曲线.

图3 生产总值神经网络权值与误差修正

图4 神经网络训练精度

测试2012年的数据为:

真实数据为:

4 结论与展望

从图3可以清晰地看到，区域生产总值的预测曲线较好地跟踪了实际水平.而图4表明，在经过12步之后系统的训练误差极小，而且从第6步之后权值迅速地趋于收敛，误差水平大大减小了，这些也说明了预测效果非常有效，且训练迅速，精度高，速度快.

本文针对这些问题，提出了整体数据使用仿生学中模拟人工智能神经网络的方法，它首先不去除一些局部维度的数据向量，保证了数据的真实性，大量并行的结构使得运算速度大大提高，其权值的自我修改与学习能力使它具有容错性和适应性，撇去在因子选择和运算中人的筛选和判断，预置终止条件而算法收敛，这是神经网络预测模型的明显优点.本文中所使用的网络泛化性能较好、收敛快，且分析结果具有很好的指导性与合理性.

［1］YAN Pingfan，ZHANG Changshui.Artificial Neural Networks and Evolutionary Computing［M］.Beijing:Tsinghua University Press，2000.

［2］LIN Min，CHO Hyeonseob.Design of direct controller for nonlinear plant based on neural network［J］.Journal of Inner Mongolia Normal University·Natural Science Edition，2002，32(2):123－127.

［3］PARK J，SANDBERG I W.Universal approximations using radial-basis-function networks［J］.Neural Computation，1991，3(2):246－257.

［4］WU Wei，ZHONG Sheng，ZHOU Guopeng.A Study on PID intelligent optimization based on radial basis function neural networks［C］∥2013，3rdInternational Conference on Consumer Electronics，Communications and Networks.Xianning:IEEE Computer Society，2013..

［5］TSUKINETU H.Extracting rules form trained neural networks［J］.IEEE Trans NN，2000，11(2):377 －389.

［6］周开利，康耀红.神经网络模型及其MATLAB仿真程序设计［M］.北京:清华大学出版社，2005.

［7］刘建.基于遗传优化RBF神经网络声纹识别研究［D］.江苏:江苏科技大学，2012.

［8］吴汪友，孙秋高.曲线拟合度分析法在公路货运回归预测中的应用［J］.海南大学学报:自然科学版，2011，29(1):49－52.

［9］王浩华，罗婷.数学建模素质评估的定量分析［J］.海南大学学报:自然科学版，2012，30(1):9－15.