分形上的拓扑及其性质

龙伦海，何 勇，梁 莉

(海南大学信息科学技术学院，海南海口570228)

首先给出了一些基本拓扑知识［1］和一些基本分形概念［2］，然后对实数集中一个给定的s-紧集E，利用其本身的离散结构和s-维Hausdorff测度分别给出了E上的2种拓扑的构造，分别称为L-拓扑和Hs-拓扑，并研究了在E上赋于2种拓扑形成的拓扑空间的关系及其性质，最后给出了E上的实值函数在2种拓扑下为连续函数所需满足的充分必要条件.本文的主要目的是在第二种拓扑下，为进一步研究E上的实函数的分数阶导数和分数阶积分建立理论基础［3－6］.

1 相关基本知识

设X是一个非空集合，T是X的子集作为元素构成的集合系，二元空间(X，T)称为是一个拓扑空间当且仅当T包含空集φ和X，且对任意并和有限交保持封闭性，T称为X上的一个拓扑，T中的元称为开集.如实数集R上的欧氏距离产生的所有开集构成的T就是R的一个拓扑，称为欧氏拓扑.如果X上的2个拓扑S和T满足S⊆T，则称S粗于T或者T比S更细，显然最粗的拓扑是{φ，X}，而最细的拓扑是X的所有子集构成的集合系.

设(X，T)是一拓扑空间.若Y是X的非空子集，令S={Y∩V/VT}，则称(Y，S)是(X，T)的拓扑子空间.若R是X中元素之间的一个等价关系，且其等价类构成的集合X/R上的集合系TR={V/π－1(V)T}形成一个拓扑，其中π是从X到X/R的自然映射，即π(x)为x所属的等价类，则称(X/R，TR)是(X，T)的关于等价关系R的商拓扑空间.

设(X，T)是一拓扑空间，若X不能分解为2个非空开集的并，则称X是连通的;若X的任意开覆盖都存在有限的子覆盖，则称X是紧的.对x X和V T满足x V，则称V是x的一个开邻域，若X中的任意2个不同点存在不交的开邻域，则称X是Hausdorff分离空间.

设f是从拓扑空间X到拓扑空间Y的一个映射，点x X满足f(x)的任意开邻域V，都存在x的一个开邻域U，有f(U)⊆V，则称f在点x处连续;若f在X的每个点处都连续，则称f是连续映射.连续映射一定将连通集映射成连通集，将紧集映射成紧集.

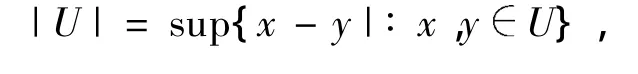
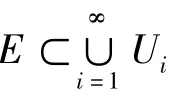
对于任意给定的集合E⊂Rn，存在唯一的s使得当t＜s时有Ht(E)=+∞，当t＞s时有Ht(E)=0，称s为E的Hausdorff维数，记为dimHE.

若s为E的Hausdorff维数，且0＜Hs(E)＜+∞，则称E为s-集，Hs(E)为E的Hausdorff测度.

2 s-紧集上的L-拓扑和Hs-拓扑

设E是实数集R中的一个Hausdorff维数为s的s-紧集，为了避免平凡性，不妨假设0＜s＜1.取T是实数集R上的欧氏拓扑，S为T在E上诱导的子拓扑，即S={E∩V/V T}，使(E，S)成为(R，T)的拓扑子空间，显然(E，S)是完全不连通的Hausdorff分离空间，即T中没有任何一个非空开集属于S.由此给出E上的另外2种逐步加粗的拓扑的定义，分别称为L-拓扑和Hs－拓扑，使得E变成连通的紧空间.首先利用空间(E，S)本身的拓扑结构对E中的点作如下分类

定义1 (1)称E中的最小点为E的左端点，最大点为E的右端点;

(2)如果E中的一个点x0满足{x0}S，则称该点为E的一个孤立点;

(3)对E中的一个点x0，若存在x0的一个开邻域V0S使得x0是V0中的最小点和x0不是其任意开邻域V的最大点，则称该点为E的一个右内端点;同样可定义E的左内端点;

(4)如果E中的一个点x0满足既不是E的左内端点，又不是E的右内端点，也不是E的孤立点，则称该点是E的一个内点.

由定义E的一个内点x0的任意开邻域V在x0的左右两边都包含有异于x0的点，E的所有内点组成的集合用N1(E)表示.

根据此分类法，E的左端点可能是孤立点，也可能是右内端点，同样右端点可能是孤立点，也可能是左内端点，除此之外的点只能是孤立点、左内端点、右内端点和内点之一.设x0是E的一个左内端点，根据定义E中的任何一个点x只能从x0的左边无限逼近于x0，若x0是右内端点，则x只能从x0的右边无限逼近于x0，而当x0是内点时，x就可以在E内从x0的两边无限趋近于x0.注意到若严格按照拓扑学的定义，把E看成是R的拓扑子集，E内无任何内点存在，因此这里定义的内点相对来说条件要弱一些，而只是聚点的一种.

在E中定义如下等价关系R1∶E中的任意2点x1，x2(不妨假设x1≤x2)在关系R1下等价当且仅当交集(x1，x2)∩N1(E)=φ，记为 x1R1x2.任取x E，记x*={y E/yR1x}为x在关系R1下的等价类.显然当x是E的内点时，x*只包含唯一的x;当x是E的左内端点时，x是x*中的最小点;当x是E的右内端点时，x是x*中的最大点;当x是E的孤立点时，x*中的点不只一个，其最大点或者是E的右端点或者是E的右内端点，相应的最小点可能是E的左内端点，也可能是左端点.

记(E/R1，SR1)是(E，S)关于等价关系R1的商拓扑空间，π1是从E到E/R1的自然映射.令E上的集合系L={(V)/V SR1}，根据商拓扑空间的定义，π1是连续映射，因此集合系L是E上的一个由R1确定的比S更粗的拓扑.

定义2 称L是E上的L-拓扑，称(E，L)是E的L-拓扑空间.

现利用E上的s-维Hausdorff测度来定义第二种拓扑.首先对E中的点作如下分类

定义3 (1)如果E中的一个点x0满足存在该点的一个开邻域V0S，使得V0与E的交集的s-维Hausdorff测度等于零，则称该点为E的一个Hs-孤立点;

(2)如果E中的一个点x0满足:对x0的任意开邻域V S有s-维Hausdorff测度Hs(V∩［x0+∞］)＞0，且存在使得该点的一个开邻域V0S使得Hs(V∩［－∞，x0］)=0，则称该点x0为E的一个Hs-右内端点;同样可定义E的Hs-左内端点;

(3)如果E中的一个点既不是E的Hs-左内端点，又不是E的Hs-右内端点，也不是E的Hs-孤立点，则称该点是E的一个Hs-内点.E的所有Hs-内点组成的集合用N2(E)表示.

从定义可以看出，E的Hs-内点的任何一个在(E，S)中的邻域都分布有正的s-维Hausdorff测度，Hs-左内端点只在其左边有正的s-维Hausdorff测度，而Hs-孤立点两边的局部范围内无正的s-维Hausdorff测度分布.

在E中定义如下等价关系R2:E中的任意2点x1，x2(不妨假设x1≤x2)在关系R2下等价当且仅当s-维Hausdorff测度Hs(［x1，x2］∩N2(E))=0.任取x E，记x＊＊为x在关系R2下的等价类，显然当x是E的Hs-内点时，x＊＊只包含唯一的x;当x是E的Hs-左内端点时，x是x＊＊中的最小点;当x是E的Hs-右内端点时，x是x＊＊中的最大点;当x是E的Hs-孤立点时，x＊＊中的点不只一个，其最大点或者是右端点或者是Hs-右内端点，相应的最小点可能是Hs-左内端点，也可能是左端点.

记(E/R2，SR2)是(E，S)的一个商拓扑空间，π2是从(E，S)到(E/R2，SR2)的自然映射.取E上的集合系H={(V)/VSR2}，根据商拓扑空间的定义，π2是连续映射，因此集合系H是E上的一个由R2确定的比S更粗的拓扑.

定义4 称H是E上的Hs-拓扑，称(E，H)是Hs-拓扑空间.

例1 设E是闭区间［0，1］上的Cantor三分集，其Hausdorff维数s0=log23，Hausdorff测度Hs0(E)=1.

令S是E上的欧氏拓扑，即由R中的所有开区间与E的交集生成的拓扑(即包含这些交集的保持有限交和可列并封闭的最小集合系).当s＞s0，因Hs(E)=0，由定义3知E中的每个点都是Hs-孤立点，从而E上的Hs-拓扑H={φ，E}是平凡的;当0＜s≤s0时，如果按E是由［0，1］3等分，去掉中间的开区间，以此类推来生成的话，E中的点可以分成2类，其中一类是由各级区间的端点形成.由定义1和定义3知，E中的点如果是某级区间的左端点，则是定义1中的右内端点和定义3中的Hs-右内端点，同样如果是某级区间的右端点，则是定义1中的左内端点和定义3中的Hs-左内端点，E中的其他点都是定义1中的内点和定义3中的Hs-内点，因此有E上的L-拓扑L和Hs-拓扑H是相等的，且是由所有R中的所有这样的开区间V与E的交集生成的拓扑，其中V一旦包含E的某个Hs-左内端点，就一定包含其右边相邻的Hs-右内端点，同样V一旦包含E的某个Hs-右内端点，就一定包含其左边相邻的Hs-左内端点.

3 L-拓扑和Hs-拓扑的性质

s-紧集E上的3种拓扑，即欧氏拓扑S、L-拓扑L和Hs-拓扑H的定义，3种拓扑具有如下关系

定理1 s-紧集E上的Hs-拓扑粗于L-拓扑，L-拓扑又粗于欧氏拓扑S，即有包含关系式H⊆L⊆S成立.

证明 E上的L-拓扑粗于欧氏拓扑S是自然成立的，下面只需证明H⊆L即可.

一方面由定义1和定义3知，对任意x E，有x在R1下的等价类x*一定包含在R2下的等价类x＊＊中;另一方面由引理1得，对任意U H，有U S且对∀x U，x＊＊⊂U成立.因此对任意的∀x U，有x*⊂x＊＊⊂U成立，然后再利用一次引理1即得U L.证毕.

根据定义得出下述引理.

引理1 设U S，有U L当且仅当∀x U有x*⊂U.同样有U H且仅当∀x U，x＊＊⊂U.

由于E在欧氏拓扑S下是非连通的紧集，在经过对S相继进行加粗后形成的L-拓扑和Hs-拓扑下，E的连通性是否改变，有下述结论.

定理2 s-紧集E在L-拓扑和Hs-拓扑下形成连通的紧集.

证明 由于对拓扑空间的拓扑经过加粗之后保持紧性和连通性不变，因此紧拓扑空间(E，S)在对拓扑相继加粗之后使得(E，L)和(E，H)仍为紧拓扑空间.所以只需证明E在L-拓扑下是连通的.

设a是E的左端点，U(a)是(E，L)中的包含a的连通分支(即包含a的最大连通开集)，下面用反证法证明U(a)=E，从而得到(E，L)是连通的.

若存在x0属于E而不属于U(a).首先由U(a)的连通性有∀xU(a)，x＜x0，否则U(a)可表示成L中2个非空开集{x U(a)/x＜x0，x}和{x U(a)/x＞x0，x}的不交并，即与U(a)是连通的相矛盾;其次由于E紧集，U(a)中的最大点x1存在，由定义1知x1一定不是E的一内点，也不是E的一右内端点，否则x1在(E，S)中的任意开邻域都包含大于x1的点，即x1的右边一定存在异于x1的点属于U(a)，当x1是E一个孤立点或左内端点时，则在x1的右边一定存在最小的点x2使得(x1，x2)∩E=φ，即有x1R1x2.由引理1得x2U(a)，与x1为U(a)中的最大点矛盾.证毕.

s-紧集E在欧氏拓扑下是不连通的Hausdorff分离空间，上述定理表明在E上对欧氏拓扑S进行加粗之后连通性变好了，但分离性又变差了，有下述性质.

定理3 s-紧集E在L-拓扑和Hs-拓扑下不是 Hausdorff分离空间.

证明 由于非Hausdorff分离空间的拓扑经过加粗之后，其分离性更弱，所以只需证明(E，L)不是Hausdorff空间即可.事实上当0＜s＜时，s-紧集E中一定存在无穷多个内端点(包括左内端点和右内端点)，E就是所有内端点和孤立点形成的子集在R中的闭包，并且除了端点之外的内端点在关系R1下的等价类中至少包含E的相邻2个点，这2个点只能同时属于或者同时不属于L的任何一个开集中，因此这2个点不能通过L中的开集分离开来，因此(E，L)不是Hausdorff分离空间.证毕.

4 s-紧集上函数在L-拓扑和Hs-拓扑下的连续性

设fE(x)是一个从s-紧集E到欧氏空间(R，T)的实函数，有下述结论.

定理4 (1)如果在E上赋于L-拓扑，那么fE(x)是连续函数的充分必要条件是:对任意的x E，fE(x)在x*上为常值函数，并且fE(x)在定义1中所定义的左内端点、右内端点和内点(即拓扑空间(E，S)中的所有极限点)处的极限值与该点的函数值相等;

(2)如果在E上赋于Hs-拓扑，那么fE(x)是连续函数的充分必要条件是:对任意的x E，fE(x)在x＊＊上为常值函数，并且fE(x)在定义3中所定义的所有Hs-左内端点、Hs-右内端点和Hs-内点处的极限值与该点的函数值相等.

证明 只证明定理4中的条件(1)成立，条件(2)的证明完全类似.

必要性 一方面若fE(x)是从空间(E，L)到(R，T)的连续实函数，则fE(x)也是从空间(E，S)到(R，T)的连续实函数，因此函数fE(x)在空间(E，S)中的每一个极限点处的极限值等于在该点处的函数值;另一方面对任意的x E，若x*包含不止一个点，且x*中存在2个不同点x1和x2使得fE(x1)≠fE(x2)，则在R中存在函数值fE(x1)的开邻域V1和fE(x2)的开邻域V2满足V1∩V2=φ，因此(V1)∩(V2)=φ，由此得(V1)和(V2)不可能同时包含x，即(V1)和(V2)中一定有一个不包含等价类 x*，从而由引理1(V1)和(V2)中至少有一个不属于L，所以fE(x)在空间(E，L)上不连续.相当于用反证法证明了函数fE(x)在空间(E，L)的每一点的等价类x*上取常值是fE(x)连续的必要条件.

充分性 设函数fE(x)在空间(E，L)的每一点的等价类x*上取常值，且在空间(E，S)中的所有极限点处的极限值等于在该点处的函数值.任取空间(R，T)的一个开集V，将证明(V)L来得到fE(x)在(E，L)上的连续性. 对此不妨假设(V)≠φ，任取 x(V)，由条件(1)一定有 x*⊂(V)成立;条件(2)保证了fE(x)是可度量拓扑空间(E，S)上的连续函数，因此(V)S.再由引理1得到(V)L.

证毕.

例2 设E是闭区间［0，1］上的Cantor三分集，著名的Cantor函数fE(x)=Hs(［0，x］∩E)就是拓扑空间(E，L)和(E，H)上的连续函数，其中s=

由定理2知，定理4中的条件(1)事实上是E上赋于拓扑后成为连通空间上的函数为连续函数所需满足的最弱条件.又因为连通紧集上的连续映射保持连通性和紧性不变，所以满足该定理条件的函数fE(x)的值域一定是欧氏空间(R，T)中的连通紧集，因而是有界闭区间，所以这样的函数一定具有有界性、最值性、介值性和一致连续性等一些很好的函数性质.

本文只讨论了R中不平凡的s-紧集E上的拓扑及性质，类似的同样可以对Rn中不平凡的s-紧集上的拓扑进行相应的研究.

［1］凯莱.一般拓扑学［M］.北京:科学出版社，1982.

［2］FALCONER K J.Fractal geometry—mathematical foundations and applications［M］.New York:John Wiley，1990.

［3］OLDHAM K B，SPANIER J.The Fractional Calculus［M］.New York:Academic Press，1974.

［4］LIANG Y S，SU W Y.Von Koch Curve and its fractional calculus［J］.Acta Mathemata Sinica，Chinese Series，2011，54(2):227－240.

［5］TATOM F B.The relationship between fractional calculus and fractals［J］.Fractals，1995，3(1):217 －229.

［6］RUDIN W.Principles of Mathematical Ananlysis［M］.New York:McGraw-Hill，1964.