基于自由搜索算法的IIR数字滤波器设计

任 伟，曾以成，陈 莉，杨 丹

(湘潭大学光电工程系，湖南 湘潭 411105)

1 概述

无限脉冲响应(Infinite Impulse Response，IIR)数字滤波器因具有计算精度高和设计阶数低等特点，在通信、生物医学、地质勘探等方面得到了广泛的应用［1］。其设计的模型是给定一个期望的频率响应Hd(ejω)，然后寻找一个稳定的传递函数H(z)，使频率响应H(ejω)在某种准则下逼近期望频率响应Hd(ejω)。近年来，许多学者把智能优化算法引入到IIR滤波器设计中，如遗传算法(Genetic Algorithm，GA)［2］、粒子群优化 (Particle Swarm Optimization，PSO)［3］算法和分布式估计算法(Estimation of Distribution Algorithm，EDA)［4］等。然而这些优化算法存在不足，如GA及其改进算法HGA(Hierarchical GA)［5］、CCGA(Cooperative Coevolutionary GA)［6］等受其全局选择机制和交叉算子的影响，种群模式缺乏多样性，容易出现早熟现象，且由于采用选择、交叉和变异等操作，结构比较复杂。与GA相比，PSO、综合学习粒子群优化算法(CLPSO)［7］和EDA简单、高效，易于实现，但同样面临早熟问题。

自由搜索算法(Free Search Algorithm，FSA)［8］作为一种新颖的启发式算法受到广泛关注，该算法模拟牛马羊等群居动物的觅食过程，于2005年提出。FSA具有更大的自由性、独立性和不确定性，在兼顾局部搜索和全局搜索、提高鲁棒性和自适应等方面有一定的提高，已经成功应用于解决复杂组合优化问题［9］。本文尝试将FSA引入IIR滤波器优化设计中，其优化模型通常是高度非线性化，且对同一个系统存在无数种相似变换。FSA的搜索机制能提高寻找IIR数字滤波器系数最优解的概率。因原型FSA的搜索半径固定不变，在多维空间后期寻优效率降低，难以寻找全局最优参数组，需要对搜索策略进行合理的调整，本文采用动态调整搜索半径，定期轴向搜索等策略，加快收敛速度，提高多维空间的后期寻优能力，进一步增大得到全局最优解的概率。

2 IIR数字滤波器的优化准则

IIR数字滤波器的实现结构总体采用直接Ⅰ型、Ⅱ型，或通过子系统级联、并联等形式。其中，二阶节级联型结构具有代表性，通过单独调整系数b1k，b2k就能单独调整滤波器的第k对零点，调整系数a1k，a2k，单独调整滤波器第k对极点，且不影响其他零点、极点。其频率响应如式(1)所示。数字滤波器的设计，就是确定系数 a1k，a2k，b1k，b2k(k=1，2，…，N)。

IIR数字滤波的性能要求以频率响应的幅度特性进行误差表征，常用的误差评价准则有最小均方误差和通带阻带纹波幅度准则。这2类评价准则都是实际频率响应幅度值与理想频率响应幅度值的逼近误差，误差越小，则滤波器的性能越好。

(1)最小均方误差准则:

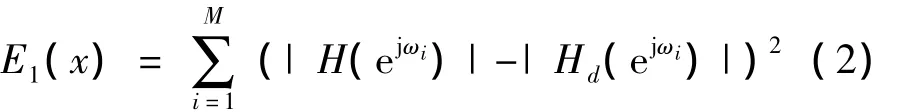
(2)通带阻带纹波幅度准则:

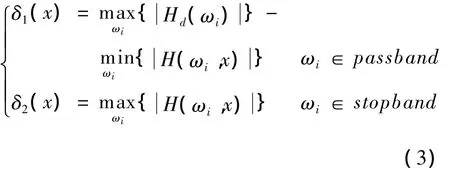
(3)2种准则结合:

其中，v1，v2，v3为权系数。

3 基于FSA的IIR数字滤波器

3.1 算法简介

FSA的基本思想［8］:以不确定应对不确定，以无穷尽应对无穷尽。个体可以在其自身的当前最佳值邻域周围搜索，也可在其他个体或群体发现的当前最佳值邻域周围搜索。个体通过信息素和灵敏度的比较在搜索步内选择坐标点，具体算法模型如下。

在搜索步内，个体的行为描述如下:

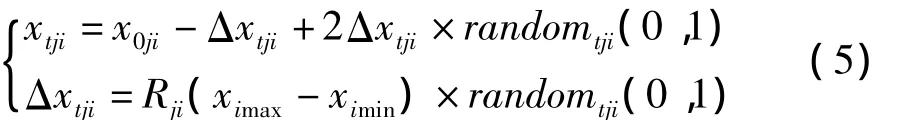
其中，j代表第 j个体(j=1，2，…，m);m 是个体的数量;i代表变量的第i维(i=1，2，…，n);n是搜索空间的维数;Rj是第j只个体在搜索空间中的领域搜索半径(Rj∈［Rmin，Rmax］);randomtji(0，1)表示(0，1)内的均匀随机数。

搜索过程中，对目标函数的简化表达式作如下规定:

其中，f(xtji)是一个个体完成搜索步以后作标记的位置。

信息素定义如下:

其中，max(fj)是当代第j只个体的最佳位置。

灵敏度定义为:

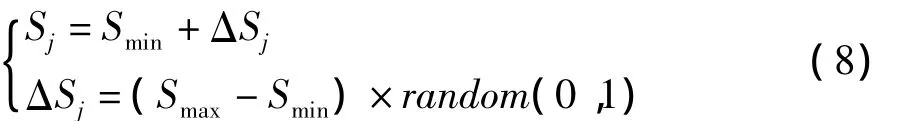
其中，Smin和Smax是灵敏度的最小值和最大值。

信息素的最小值和最大值分别为Pmin，Pmax，规定:Smin=Pmin，Smax=Pmax。

一轮搜索结束后，确定下一轮搜索的起始点。

3.2 改进搜索策略

3.2.1 实时调节搜索半径

FSA原型中搜索半径R是固定的，若其取值较大，则搜索时间长、收敛精度低;若取值较小，则搜索范围小，容易出现早熟现象，尤其在多维环境中，算法对半径R非常敏感。本文首先采用分段给R赋值，弥补因种群规模不足而导致局部搜索的缺陷，增加种群的多样性，确保个体在参数空间广泛分布;然后动态调整R，使Rj(t)递阶减小，提高在多维空间后期的寻优效率，其变化规律如下式所示:

其中，g是当前搜索代数;Rmin是最小搜索半径;ρ1是收缩系数:1≥ρ1＞0，当ρ1=1时，即为基本FSA。

3.2.2 定期轴向搜索

当搜索半径逐步减小时，可能进入局部收敛，导致早熟。为了提高算法的局部搜索能力，需要作定期轴向搜索，即每迭代一定次数后对当前最优个体进行一次增大搜索半径的轴向搜索，这样可以加快收敛速度，更易得到全局最优解，另外轴向搜索增强了种群的多样性。由于一次轴向搜索的计算量比较大，因此采用了定期轴向搜索。

轴向搜索是指得到当前最优个体后，以当前最优个体为中心，进行轴向搜索，如:以当前最优个体xji为中心，以α为步长进行搜索，令:

如果x′ji的值超出规定范围，就取最大值或者最小值。比较目标函数 f(x′ji)和 f(xji)，若 f(x′ji)＜f(xji)，则用 x′ji取代 xji，否则坐标不变。

3.3 算法步骤

FSA优化设计IIR数字滤波器的实现步骤如下:

(1)初始化参数，包括种群规模、种群个体的初始坐标、收缩系数ρ1、参数空间大小等。

(2)初始搜索。根据式(5)～式(7)生成初始信息素，释放初始信息素Pj→Xk，得到初始搜索结果Pk，Xkp。

(3)动态调整搜索半径R。

(4)计算灵敏度。按照式(8)计算灵敏度Sj。

(5)确定新的始点。选择新一轮搜索的起始点，x′0j=xk(Sj，Pk)。

(6)计算搜索步。计算目标函数ftj(x′0j+Δxt)，其中，Δxt由式(5)计算。

(7)若迭代次数达到规定周期，则对当前最优个体进行轴向搜索。

(8)释放信息素。按照式(8)计算信息素Pj;按照式(9)释放信息素Pj→xk，得到本次搜索结果。

(9)终止判断。若满足终止条件则输出搜索结果;否则，跳转步骤(2)。

4 实验分析

为了验证FSA设计IIR数字滤波器的有效性和可行性，在计算机上进行仿真实验，并与已有的设计方法进行比较。

例1 在最小均方误差准则下，设计一个低通IIR数字滤波器，阶数为2n=6，［0，π］内的频率采样点M=21，其技术指标为:

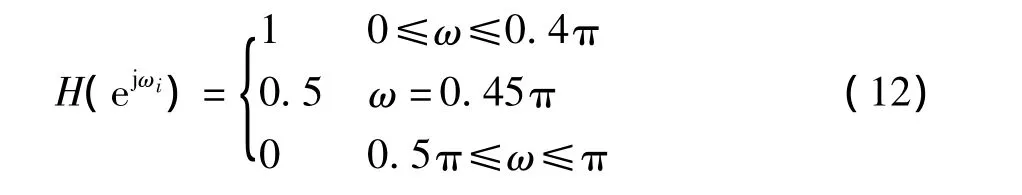
图1显示了本例在最小均方误差准则下，FSA，GA，PSO以及IA设计所得IIR低通滤波器幅频响应曲线。4种优化算法的种群大小都为50，最大迭代次数均为500。从图1可以看出，FSA设计的滤波器优化结果比较理想，通带比较平坦，阻带衰减较大，且过渡带窄。4种算法具体优化结果比较如表1所示。由表1可知，在通带和阻带纹波方面，FSA比其他3种优化算法的波动都小;FSA所设计的滤波器均方误差可以达到10－4数量级，且阻带衰减为41.49 dB，比GA提高了13.67 dB。这种优化准则比较适用于对频带误差能量要求比较高的情形。

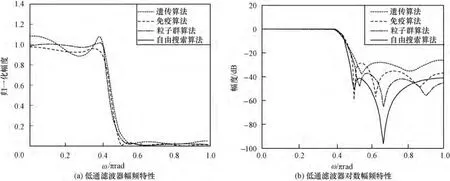
图1 IIR低通滤波器幅频响应曲线

表1 4种算法的优化结果比较

例2 为了进一步验证FSA的优越性，在通带阻带纹波幅度准则下，设计一个低通IIR数字滤波器，设计指标来源于文献［4］，其技术指标为:

FSA 算法、HGA算法［5］、CCGA 算法［6］、IIA(Improved Immune Algorithm)算法［10］以及EDA算法［4］设计本例所得滤波器幅频响应曲线如图2所示。从图中可以看出，无论在通带还是阻带，FSA算法设计的滤波器性能都比其他4种算法有较大的进步，显示了良好的性能。具体优化结果比较如表2所示。这种优化准则比较适合设计对频带纹波要求比较高的滤波器。

图2 IIR低通滤波器幅频响应曲线

表2 5种算法的优化结果比较

例3 FSA与经典滤波器设计方法巴特沃斯、切比雪夫Ⅰ、切比雪夫Ⅱ、椭圆设计作比较。滤波器设计指标采用例2中的设计指标。设计准则为均方误差准则和通带阻带纹波幅值准则相结合，具体形式如式(4)所示，其中，v1∶v2∶v3=1∶8∶8。表 3 是 5 种设计方法的性能对比。在相同滤波器阶数的条件下，FSA的均方误差比其他4种都小，比ELTC提高11倍多，可以实现对频带误差要求高的IIR数字滤波器设计。在通带和阻带纹波方面，FSA比其他设计方法的波动都小，且通过调整权系数的比值，可以优化设计不同性能要求的IIR数字滤波器。

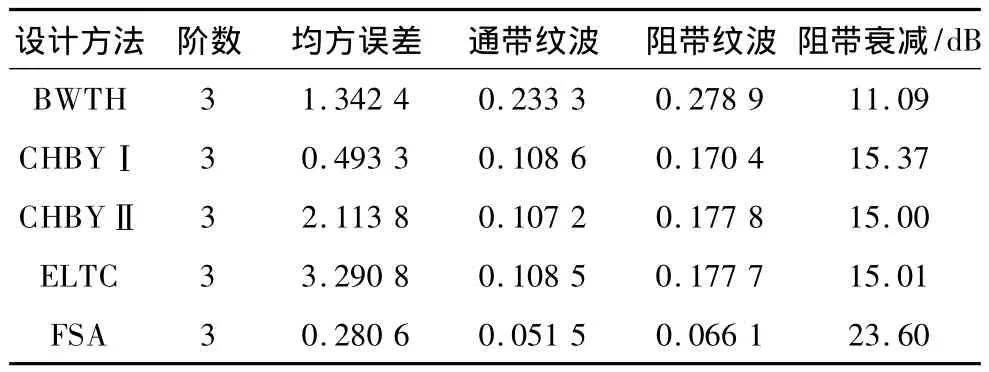
表3 本文设计方法与经典设计方法比较

5 结束语

本文将改进的自由搜索算法应用于无限脉冲响应(IIR)数字滤波器的优化设计，在3种不同优化准则下，都显示了一定的优越性。同时，仿真结果表明，最小均方误差准则比较适用于对频带误差能量要求比较高的情形，最小通带阻带纹波幅值准则比较适用于频带纹波要求比较高的情形，且2种准则相结合，既可以满足通带和阻带纹波要求，又可以进行频带误差能量优化。通过调整权系数的比值，可以实现不同性能要求的滤波器。但本文算法性能只在Matlab仿真软件中实现，还未能够在硬件上实现，这将是下一步的研究方向。

［1］Lai Xiaoping，Lin Zhiping.Minimax Phase Error Design of IIR Digital Filters with Prescribed Magnitude and Phase Responses［J］.IEEE Transactions on Signal Processing，2012，60(2):980-986.

［2］李建华，殷福亮.设计IIR数字滤波器的遗传优化算法［J］.通信学报，1999，17(3):1-7.

［3］张旭珍，马红梅，薛鹏骞.基于改进粒子群优化算法的IIR数字滤波器设计［J］.计算机工程与设计，2011，32(8):2853-2856.

［4］Li Yuquan，Zhang Gexiang.A Modified Estimation of Distribution Algorithm for Digital Filter Design［J］.Romanian Journal of Information Science and Technology，2012，15(1):50-62.

［5］Tang K S，Man K F，Kwon S，et al.Design and Optimization of IIR Filter Structure Using Hierarchical Genetic Algorithms［J］.IEEE Transactions on Industrial Electronics，1998，45(3):481-487.

［6］Yang Yu， Yu Xinjie.Cooperative Coevolutionary Genetic Algorithm for Digital IIR Filter Design［J］.IEEE Transactions on Industrial Electronics，2007，54(3):1311-1318.

［7］赵新安，陈 明，张钟华，等.采用综合学习粒子群算法的有限脉冲响应数字滤波器设计［J］.西安交通大学学报，2012，46(8):71-75.

［8］Penev K，Littlefair G.Free Search——A Comparative Analysis［J］.Information Sciences，2005，172(1/2):173-193.

［9］毕晓君，李云刚.基于自由搜索算法的图像分割研究［J］.信息技术，2010，(7):97-100.

［10］Tsai J T，Chou J H.Design of Optimal Digital IIR Filters by Using an Improved Immune Algorithm［J］.IEEE Transactions on Signal Processing，2006，54(12):4582-4596.