基于EFDR编码压缩的非确定位填充算法＊

郭东升，唐 敏，吴铁彬，刘衡竹

（国防科学技术大学计算机学院，湖南 长沙 410073）

1 引言

随着集成电路制造工艺的进步和芯片集成规模的急剧增加，芯片测试数据猛增，导致测试成本急剧上升，如何降低测试数据的存储开销并缩短测试时间是当前学术界研究的热点。

减少测试数据的存储开销可以通过BIST（Build－In Self－Test）结 构［1］和 测 试 数 据 压 缩 技 术来实现［2］。BIST结构需要嵌入到芯片中，常常和片上的测试数据产生模块联合使用。虽然BIST结构可以大幅度地减少需要存储的测试数据数量，不过利用BIST结构的测试时间会增加，而且BIST结构会改变测试电路的物理结构，增加约束条件，这些都限制了BIST结构的使用。而测试数据压缩技术则不需要对电路结构进行改变，可以独立于测试电路对测试数据进行压缩，从而减少测试数据的存储开销。

EFDR算法［3］是一种典型的基于编码压缩的测试数据压缩算法。EFDR算法考虑对连续0游程和连续1游程分别编码，具有算法简单、压缩解压缩结构小、压缩效率高等特点。

除了编码压缩算法的研究，针对非确定位填充的研究也很重要。由于测试数据中的非确定位数量极大［4］，合理地对非确定位填充会提高压缩算法的压缩效率。

本文以EFDR算法为基础，研究EFDR算法的非确定位填充要求，提出了针对EFDR编码压缩算法优化的非确定位填充算法ESA（EFDR－Suited X－filling Algorithm）。基于ISCAS’89标准电路［5］的实验结果表明，该算法在不提高测试功耗的前提下，提高了EFDR算法的压缩效率，缩短了测试时间。

2 优化的EFDR算法的非确定位填充技术

2.1 非确定位填充算法介绍

测试数据中的非确定位是非常多的，常常占测试数据总数的70%以上，更有些测试数据中的非确定位数占到测试数据的90%以上（见表1），所以合理填充非确定位可能会对测试数据压缩效果有所提高。

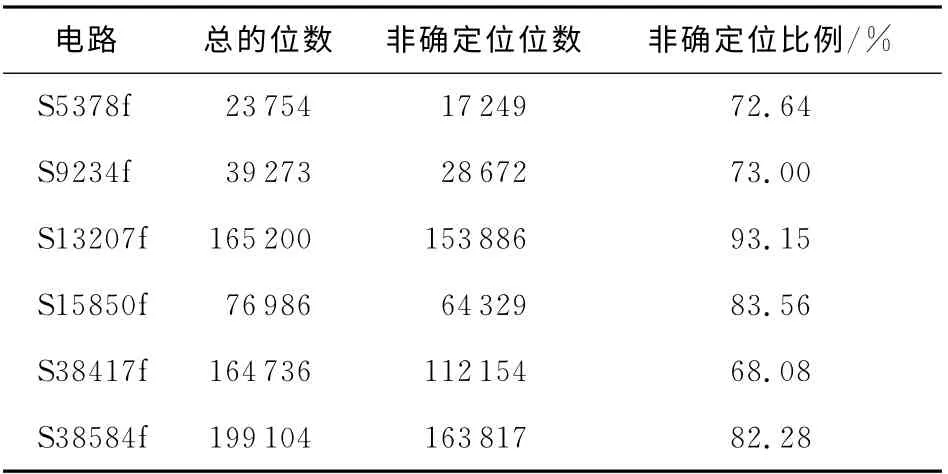
Table 1 Ratio of X in test data表1 非确定位在测试数据中所占的比例

传统的非确定位填充技术主要包括全0填充和全1填充，即分别对非确定位全部填充0或者全部填充1，除此之外还有一些改进的非确定位填充算法，如：最少传输跳变填充算法MT－filling（Minimum－Transition－fill）［6］、邻 近 位 相 同 填 充 算 法Adjacent－filling［7］。MT－filling填 充 算 法 在 填 充时，如果非确定位序列两边的确定位相同，非确定位填充值为相同确定位的值，否则随机填充0或者1；在Adjacent－filling算法中，非确定位的填充与传输方向上的临近确定位相同。

对于测试数据0XXX1X0X1XXX1X0

全0填充为：000010001000100

全1填充为：011111011111110

MT－filling为：000011001111100

Adjacent－filling为：000011001111110

2.2 EFDR算法的非确定位填充方法

EFDR编码压缩算法的非确定位填充算法和这些算法不同，EFDR在填充非确定位时，考虑了EFDR算法的特点，其编码字见表2。EFDR编码压缩算法对以1结尾的0游程或以0结尾的1游程进行编码，按照游程的长度范围将游程划分到不同的组中，编码字随分组编号的增加而递增，组编号小的编码字短，组编号大的编码字长，增幅为两位。

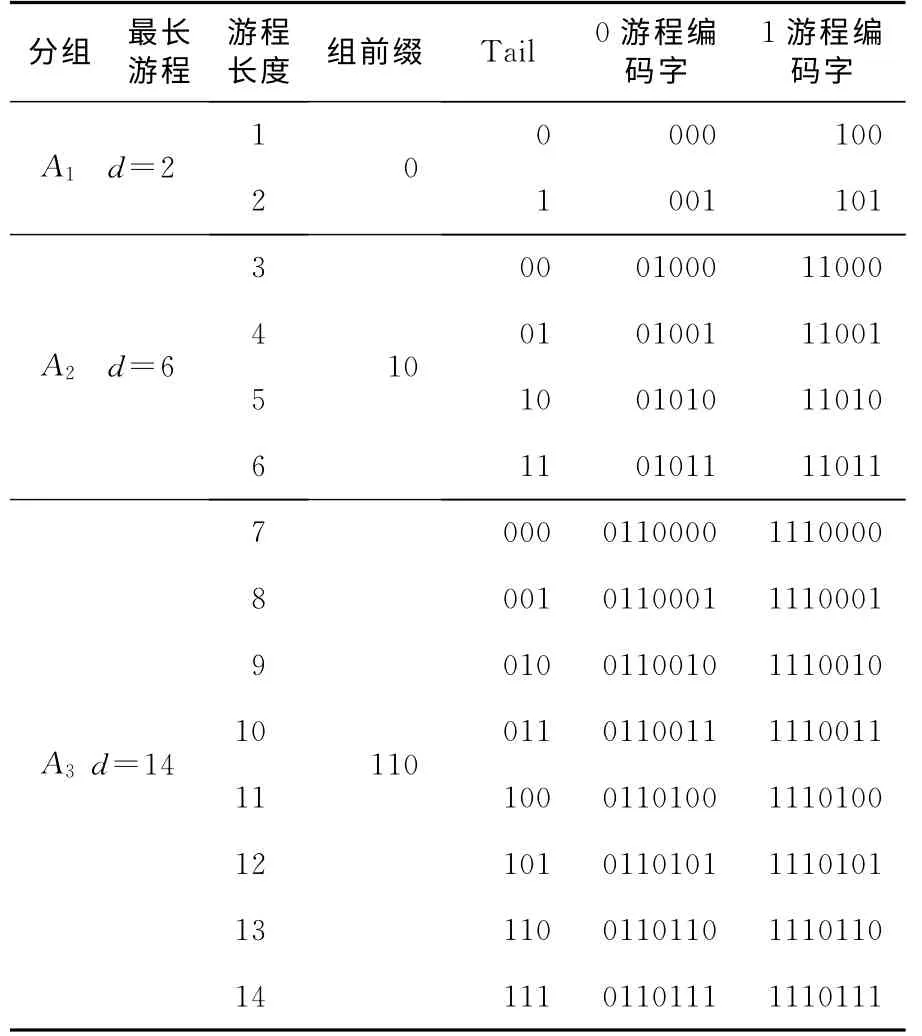
Table 2 Code word of EFDR code表2 EFDR编码算法编码字表

由表2可知，测试数据游程越长，编码效率越高。故EFDR算法的非确定位填充规则如下：

（1）当非确定位游程两边的确定位相同时，非确定位填充值为该确定位值。

（2）当非确定位游程两边的确定位不相同时，沿测试数据的传输方向：

①当非确定位游程前的确定位游程长度大于1时，非确定位的填充值与前边的确定位值相同；

②当非确定位游程前的确定位游程长度为1时，非确定位填充值与后边的确定位值相同。

依据上述填充规则，对于测试数据：

1XXXX1 11XXXXX0XXXX1 1XXX0 0XXXX1XX0XXXX01

EFDR算法的填充结果为：111111 11111110 11111 11110 000001 000000001

2.3 EFDR填充算法的缺陷

EFDR算法对非确定位的填充已经考虑到了其算法的编码特点，不过由于每个分组都包含一定的游程长度，所以对于包含非确定位的测试数据段，不同的非确定位填充方法，得到的编码游程分组可能不同。

例如，对于测试数据序列：

11111XXX00XXXXXXXXXXX1

使用EFDR算法的填充为：

111111110 0000000000001

所属编码分组都为A3，需要的编码字长为14位。

考虑第一个非确定位游程，由表2可知，如果将第一个非确定位游程的前一个非确定位填充为1，后两个确定位填充为0，这样填充之后得到的测试数据可以划分为一个属于A2组的连续1游程和一个属于A3组的连续0游程，即：

1111110 000000000000001

压缩该测试数据段需要的压缩编码总长为12位，相对于EFDR算法的填充方法少了2位。

2.4 优化的非确定位填充算法

本文提出的非确定位填充算法按照以下的填充规则填充：

规则1 当非确定位两边为1时，即测试数据序列形如：1XXXX1时，非确定位填充为1；

规则2 当非确定位两边为0时，即测试数据序列形如：0XXXX0时，非确定位填充为0；

规则3 当非确定位两边的确定位不同时，即测试数据形如：1XXXXX0或0XXXXX1时，考虑两边确定位的情况进行填充。

本文提出的非确定位（ESA）填充算法可以分为三步：首先对满足规则1和规则2情形的非确定位进行填充；之后将待填测试数据进行预处理，得到测试数据游程类型数组T＝｛ti｝，确定游程长度数组L＝｛li｝以及非确定位游程长度数组M＝｛mi｝；最后利用数组T、L、M对非确定位游程进行划分和填充，得到待压缩测试数据游程长度数组S＝｛si｝。

例如，对于测试数据：11XXX000XXX110，预处理得到的数组T＝｛1，0，1，0｝，L＝｛2，3，2，1｝，M＝｛3，3，0，0｝；之后将M中的每一个元素mi分割成ai与bi之和，mi＝ai＋bi，其中，非确定位游程中的前ai个非确定位填充和ti相同，后bi个非确定位填充和ti＋1相同；最终得到的待压缩测试数据游程长度数组S＝｛si｝，si＝bi－1＋li＋ai。

由以上讨论可知，对非确定位游程长度mi的划分是ESA填充算法的核心，考虑EFDR算法的非确定位填充要求，根据测试数据的特征数组T、L，非确定位游程长度mi的划分方法见表3。

Table 3 Segmentation of mi表3 算法中mi的划分方法

非确定位填充算法的主要步骤如下：

利用ESA填充算法对非确定位填充，可以得到更短的压缩字，例如，对于如下长度为60位的测试数据段：

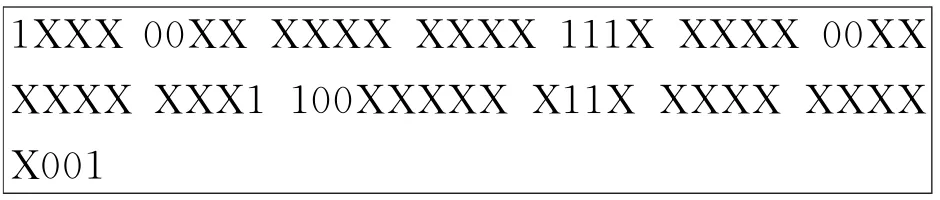
利用EFDR算法的填充算法得到的压缩后的需要存储的测试数据为（共46位）：

利用ESA填充算法得到的压缩后的需要存储的测试数据为（共40位）：

相对于利用EFDR算法的填充方案，ESA填充算法可以减少压缩数据的长度，提高压缩效率。

3 实验结果与分析

3.1 压缩效率分析

为了验证填充算法ESA的有效性，本文使用Matlab实现该算法，基于ISCAS’89基准测试电路，Mintest ATPG［8］产 生 的 测 试 向 量 集，使 用ESA填充算法填充测试数据中的非确定位；再利用EFDR算法压缩测试数据，得到的测试数据压缩效率与原EFDR算法的压缩效率比较见表4。假设TD是原始的测试数据总位数，TE是压缩后的编码字的总位数，压缩效率CR可以表示如下：

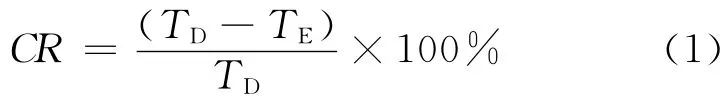
Table 4 Comparison of compression ratio between EFDR and EFDR＋ESA表4 改进填充算法压缩效率比较

表4中，TD代表原始测试数据量，EFDR代表使用EFDR的填充算法得到的压缩后的测试数据数量TE和压缩效率CR，EFDR＋ESA表示使用ESA填充算法得到的压缩后的测试数据数量TE和压缩效率CR。由Improvement的数据可知，利用ESA填充算法时，EFDR编码压缩的压缩效率提高1.14%，证明ESA填充算法是有效的。其中，对于电路S9234和电路S38417的提高相对较高，这说明，ESA所针对的特征非确定位在这两个电路中占的比例较大。

3.2 功耗分析

由于本文仅对填充算法进行了优化，并未对压缩和解压缩结构做任何改变，所以本节只考虑可能会受到填充算法改变而影响到的测试数据的翻转功耗。

由前文可知，本文提出的算法只针对非确定位两边确定位不相同的情形，即0XXXX1或1XXXX0这两种情形，对于这种情形的填充方法，由表3可知，可以分为以下几种情况：

非确定位与前边确定位相同；

非确定位与后边确定位相同；

非确定位前一部分与前边确定位相同，后一部分与后边确定位相同。

例如，对于0XXXXX1，本文得到的填充方案只有：00000001、01111111、00011111这三种情况，而这三种情况都不会增加该序列的01和10的翻转数，故本文提出的填充算法不会增加测试数据的翻转率。

3.3 时间开销分析

本节分析ESA填充算法对测试时间开销的影响，按照文献［9］的方法，测试时间可以通过以下方法计算：

假设频率比率α＝fCUT／fATE，fCUT是被测试电路的工作频率，fATE是测试设备的时钟频率。假设测试集有N个编码字C1～CN，每个编码字的长度为Wi，则αmax［9］为：

其中，Hi－1为Ci－1解压缩得到的测试数据的长度。

如果α＜αmax，由于解压缩一个编码字用的时间比从自动测试设备ATE（Automatic Test Equipment）传输一个编码字到被测电路CUT（Circuit Under Test）所用的时间长，这时ATE会等CUT几个时钟周期，则测试时间TAT［9］为：

如果α＞αmax，可以得到为：

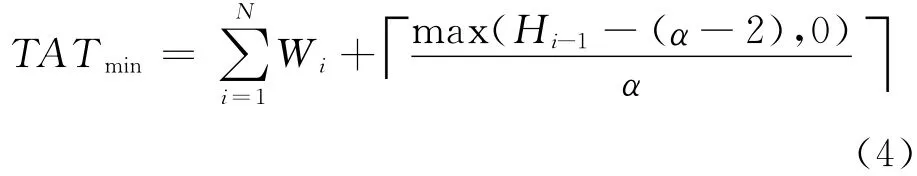
表5给出了使用ESA填充算法时的时间开销和使用EFDR算法的填充算法的时间开销对比，频率比率α从4～10，表格的第三列为使用EFDR算法填充的时间开销，第四列是使用ESA填充算法时的时间开销，最后一列Improvement表示使用ESA填充算法相对于使用EFDR填充算法的时间开销的节省幅度。由表5中数据可知，相对于EFDR的填充算法，ESA填充算法可以适当减少时间开销，减少幅度大都在1%～2%，当频率比率α增大时，提升幅度相应也会提高。

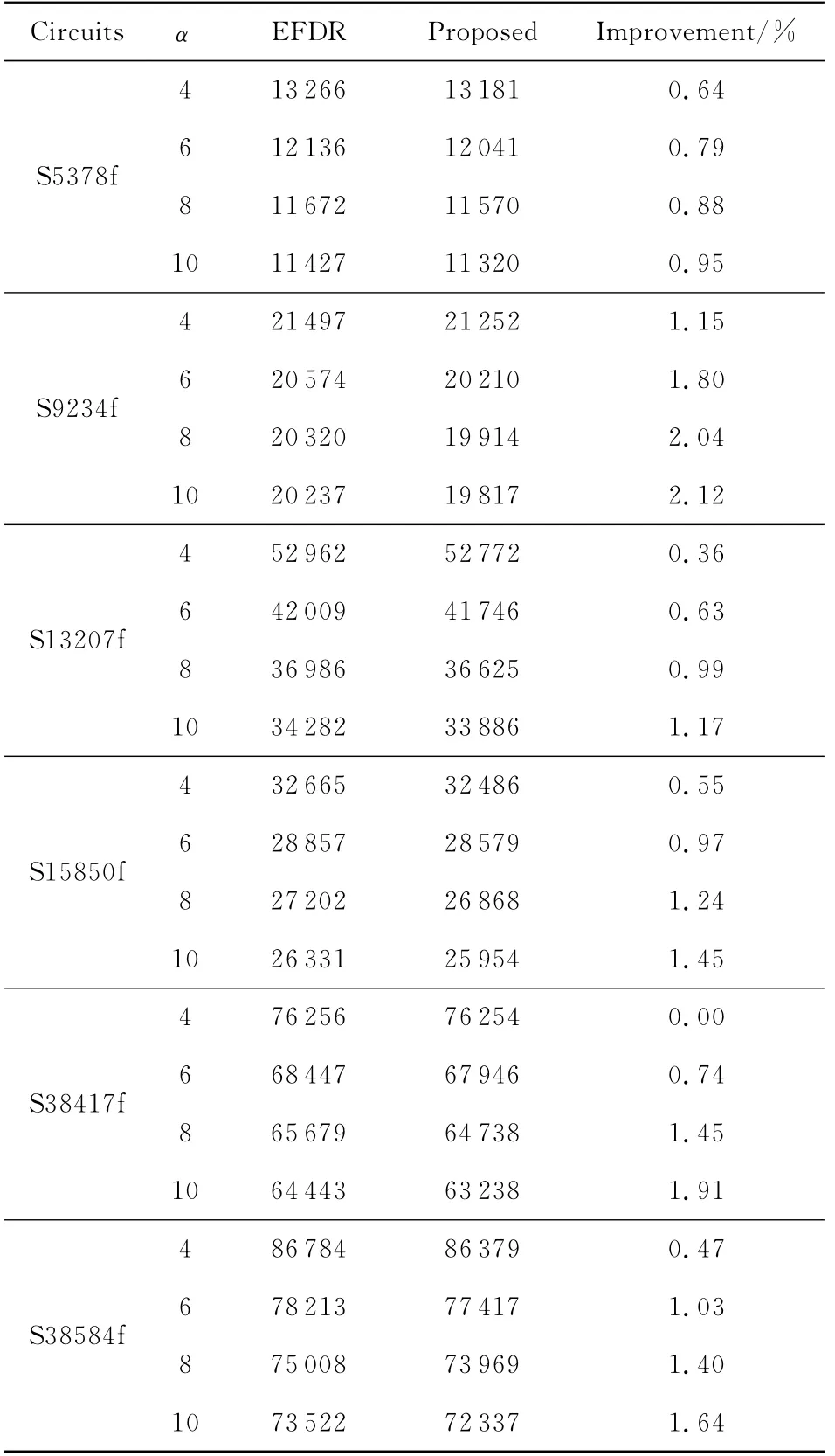
Table 5 Comparison of test time表5 不同填充算法测试时间开销比较

4 结束语

本文提出了一种新的基于EFDR编码压缩算法的非确定位填充算法，该算法针对测试向量中可能出现的一些特定情况进行优化改善。针对ISCAS’89基准测试电路的实验结果表明，在使用本文提出的填充算法对非确定位进行填充时，压缩效率相对于原始EFDR算法提高了1.14%，时间开销相对减少了2%左右，并且本算法不会增加测试向量的翻转率，即不会引入额外的测试功耗，同时硬件开销与原有EFDR算法一致。

［1］ McCluskey E J.Built－in－self－test structures［J］.IEEE Design ＆Test of Computers，1985，2（2）：29－33.

［2］ Touba N A.Survey of test vector compression techniques［J］.IEEE Design ＆Test of Computers，2006，23（4）：294－303.

［3］ EL－Maleh A H.Test data compression for system－on－a－chip using extended frequency－directed run－length code［J］.IET Computer Digital Technology，2008，2（3）：155－163.

［4］ Miyase K，Kajihara S.Don’t care identification of test patterns for combinational circuits［J］.IEEE Transactions on Computer Aided Design of Integrated Circuits and Systems，2004，23（2）：321－326.

［5］ Bglez F，Bryan D，Kozminski K.Combinational profiles of sequential benchmark circuits［C］∥Proc of International Symposium on Circuits and Systems，1989：1924－1934.

［6］ Sankaralingam R，Touba N.Multi－phase shifting to reducing instantaneous peak power during scan［C］∥Proc of the 4th IEEE Latin American Test Workshop，2003：78－83.

［7］ Girard P，Nicolici N，Wen X.Power－aware testing and test strategies for low power devices［M］.New York：Springer，2009.

［8］ Hamzaoglu I，Patel J H.Test set compaction algorithms for combinational circuits［C］∥Proc of IEEE International Conference on Computer－Aided Design，1998：283－289.

［9］ Gonciari P T，Al－Hashimi B M，Nicolici N.Improving compression ratio，area overhead，and test application time for system－on－a－chip test data compression／decompression［C］∥Proc of Design，Automation and Test in Europe Conference and Exhibition，2002：604－611.