云计算环境下带安全约束的工作流调度问题的研究＊

马俊波，殷建平

（国防科学技术大学计算机学院，湖南 长沙 410073）

1 引言

云计算作为一种新兴的计算模式，以其特有的随需自助式服务、广泛的网络访问、共享的资源池、快速弹性能力、服务的可度量性等特性［1］，正逐渐地深入到互联网生活的各个方面。云服务提供商通过把众多的计算机软硬件资源整合为虚拟的资源池为用户提供服务，并通过与用户签订的服务水平协议SLA（Service Level Agreement），向用户承诺服务质量QoS（Quality of Service）。用户可以根据自身的需要，向云服务提供商申请相应的计算资源，并在使用完毕后释放这些资源以供其他用户使用。由于计算资源和用户规模巨大，且具有快速弹性变化的特性，使得云平台下的资源调度问题一直是该领域研究的热点问题。

当前对资源调度问题的研究主要集中在减少完成时间、降低用户开销和提高负载均衡等问题上，很少去考虑用户对安全和隐私等约束条件的需求。然而，云计算平台从诞生之日起，其安全问题就一直是广大用户和云服务提供商们关注的焦点问题之一。因此，在云计算资源调度的过程中加入安全约束，满足用户在资源调度过程中对安全的QoS需求就具有十分重要的意义。

2 相关工作

云计算中，许多大型的应用程序通常都是由一组有数据依赖关系和执行顺序约束的子任务组成，这类任务通常被抽象为工作流的形式。这种工作流模型在云计算的资源调度研究中被广泛地使用［2］。

Abrishami S等人［2］以用户给定的最后完成期限为主要约束条件，提出了两个多项式时间复杂度的算法，使它们能够满足大规模的工作流程序的调度任务，并在实际的科学计算工作流上进行了实验，取得了很好的性能。Liu K等人［3］则是以任务的花费为主要约束条件，针对实例密集型的工作流任务，在综合考虑任务的执行时间和执行开销的基础上，提出了一种满足用户预算的调度算法；并且实验表明，该算法不仅能够消减任务的平均执行成本，还能在满足用户预算的条件下缩短任务的平均执行时间。Rao J等人［4］充分考虑了云环境下的动态变化特性，为了保证Web服务器在给定的响应时间的条件下对虚拟资源进行分配，提出了一种自适应的模糊控制方法；并在此基础上进一步设计了一个两层的QoS框架，这个框架在性能和功耗控制方面，对多目标QoS控制和服务差异化管理具有很好的性能优势。Wu Z等人［5］以云计算的这种以市场为导向的业务模式为基础，提出了一种以市场为导向的分层调度策略，以满足用户的各项QoS需求；在此基础上，为服务层提出了一种基于包的随机调度算法，并使用了三个具有代表性的智能优化算法作为启发式，讨论了它们的各项性能。Ergu D等人［6］根据现有的可用资源和用户偏好，使用成对比较矩阵技术和层次分析方法，为任务划分了等级，并提出了一种面向任务等级的资源分配模式，给出了在各种任务中算法对资源调度过程中分配和改善的一致性比率。

这些文献分别从不同的角度对云环境下的资源调度问题进行了深入的研究，提出了资源调度的方法和策略，但正如前文所提到的，这些研究都很少去考虑用户对安全的QoS需求。

3 系统模型

3.1 符号与说明

本文使用的相关术语和符号定义如下：

（1）计算资源。

在云计算模型中，实际的物理资源通过虚拟化技术虚拟化为资源池来进行统一的管理和分配，向用户提供透明的计算服务和数据存储功能，屏蔽了物理层的部署细节。因此，本文提到的计算资源是由当前云平台可用虚拟机组成的，即R＝｛vm1，vm2，…，vmn｝，n为虚拟机总数。每台虚拟机的属性包括计算能力MIPS（Million Instructions Per Second）、存储能力、内存、带宽等。本文只考虑计算能力这一属性，令计算能力P＝｛Pi｝，其中i∈｛1，2，…，n｝，元素存储的是第i台虚拟机对应的计算能力，同时每台虚拟机都有一个特定的安全等级SR（Security Rank），令SR＝｛srj｝，则第j个虚拟机的安全等级就表示为srj，其中j∈｛1，2，…，n｝。

（2）通信矩阵。

虚拟机之间通过网络相互连接，两台虚拟机之间的最小通信代价记录在通信矩阵Comu＝［cmij］中，其中i，j∈｛1，2，…，n｝，矩阵中的元素cmij表示从虚拟机vmi到vmj之间传输单位数据所需的最小时间，并且当i＝j时，令cmij＝0。

（3）计算任务和原子操作。

一个计算任务通常可以分解为一组相互约束的原子操作，即T＝｛O1，O2，…，Om｝，m为原子操作总数。每个操作通常由一台虚拟机完成，并有输入数据和输出数据。操作之间有执行先后顺序的约束，即工作流约束。每个操作都有特定的指令长度MI（Million Instructions），定义指令长度L＝｛Li｝，其中i∈｛1，2，…，m｝，元素Li存储的是第i个操作对应的指令长度，同时每个操作都有相应的安全等级需求SD（Security Demand），令SD＝｛sdj｝，则第j个操作的安全需求就表示为sdj，其中j∈｛1，2，…，m｝。

（4）工作流约束。

工作流约束一般使用有向无环图DAG（Directed Acyclic Graph）来表示，有向无环图中的节点表示子任务，边表示数据的依赖关系和通信的开销。定义工作流表示为有向无环图G（O，E），其中O为节点集合，对应于计算任务的操作集合，即O＝｛O1，O2，…，Om｝；E为边的集合，每条边都有确定的方向和权值，用来表示操作之间的执行先后的约束和数据传输量。

对于边（Op，Oq）∈E，表示当Op完成并把数据传输到Oq后，Oq才能开始执行，并且从Op输出并传输到Oq的数据量为该边的权值，称Op是Oq的前驱节点，Oq是Op的后继节点。如图1为一个包含了15个操作的工作流约束。

（5）调度方案。

对于任务T＝｛O1，O2，…，Om｝的调度方案S＝｛s1，s2，…，sm｝，其中sk表示操作Ok分配到的虚拟机编号，sk∈｛1，2，…，n｝。

Figure 1 A workflow task with 15operations图1 包含15个操作的工作流任务

3.2 安全约束模型

互联网发展至今，已经拥有了一系列的安全技术来应对安全问题，如加密解密技术，认证、授权和审计技术，防火墙技术，安全接入技术等［7］。根据使用技术的安全强度，以及虚拟机上运行的软件的安全程度，可以为虚拟机划分相应的安全等级。同时，根据操作的敏感程度、访问控制、操作执行所需的环境以及用户的需求等，可以为操作划分相应的安全需求sd。本文把安全定性地划分为五个等级：

很高→5；高→4；中→3；低→2；很低→1

常见的安全约束模型有三类［8］：

（1）安全型：在进行调度时，仅把操作分配到能够满足安全需求的虚拟机上，即当且仅当sdi≤srj时，把操作Oi分配到虚拟机vmj上，其中i∈｛1，2，…，m｝，j∈｛1，2，…，n｝。

（2）冒险型：在进行调度时，不考虑安全约束，直接把操作分配到可用的虚拟机上。

（3）r－risky型：在进行调度时，最多冒r的风险，其中r表示发生风险的系数，用来衡量发生风险的概率。并且当r＝0时，对应于安全型；当r＝1时，对应于冒险型。

冒险型的调度方式过于激进，而安全型调度方式一般来讲难度较大，并且需要花费较大的代价才能实现，特别是当任务的实时性要求较高时，为了减少任务的完成时间，满足用户对任务完成截至期限的需求，一般采用r－risky型调度方式。这样一方面保证了任务的安全，另一方面能够降低调度的代价，并在一定程度上减少完成任务所需要的时间。

本文定义的安全约束由两部分组成：

（1）对于单个操作Oi和其分配到的虚拟机vmj，要求sdi－srj≤θ，θ∈｛0，1，2，3，4，5｝，其中θ为安全等级跨度，并且当sdi－srj≤0时，认为该调度是安全的。例如，当θ＝2时，对于安全需求为4的操作，可以分配到安全等级为2、3、4、5的虚拟机上，并且当把该操作分配到安全等级为4、5的虚拟机上时，认为该调度是安全的。

（2）对于任务T＝｛O1，O2，…，Om｝的整体调度方案S＝｛s1，s2，…，sm｝的风险概率由公式（1）求得，并要求该调度方案的P（risk）≤r：

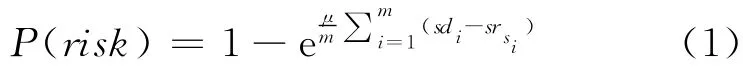
其中μ为常数，根据任务对风险的承受程度适当选择。

则安全约束就可以表示为一个二元组Secu＝（θ，r）。

3.3 问题定义

由于许多最优调度问题是NP－hard问题［2］，一般而言为了简化和解决调度问题，会做出一定的假设条件。本文使用的假设条件如下，这些假设也是该领域内常用的假设条件：

（1）当前驱操作完成并把数据传送到后继操作时，后继操作立即开始执行。

（2）虚拟机每次只能运行一个操作，其余操作进入排队队列。

（3）虚拟机创建的时间为零或有统一的时间间隔。

（4）每个操作只能分配到一个虚拟机上。

（5）一旦一个操作分配给了一个虚拟机，那么它将连续运行，直到操作结束。

（6）操作只在开始和结束的时候产生数据通信。

工作流约束G（O，E）可以用工作流矩阵F＝［fpq］来表示，当存在边（Op，Oq）∈E时，把边的权值保存到矩阵的元素fpq中，当Op和Oq之间没有边连结时，fpq＝0。对于图1所示的工作流约束，可以表示为如下所示的工作流矩阵F：

任务T＝｛O1，O2，…，Om｝中的操作Oi，其完成时间由两部分组成，即接收输入数据所需要的时间开销，和操作在其分配到的虚拟机上运算所需要的时间开销。当两个操作部署在同一台虚拟机上时，数据传输时间忽略不计，这可以通过把通信矩阵Comu中的对角线元素置0来实现，即当i＝j时，令cmij＝0。对于任务的一个调度方案S＝｛s1，s2，…，sm｝，定义操作Oi的完成时间为COi，其计算公式如下所示：

定义cvmi为虚拟机vmi执行完分配到其中的所有操作所需要的时间，即Cvmi＝∑COk，当且仅当Ok分配在vmi上时。那么整个任务的完成时间就为耗时最长的虚拟机的执行时间，即Ccomp＝max｛Cvmi｝。若要使任务的完成时间最小，则是求Ccomp的最小值，则优化目标可表示为：f＝min｛Ccomp｝。

那么带有安全约束的资源调度问题可定义为：在满足约束F、Comu、Secu的条件下，把任务T部署到资源R上，并达到优化目标f。可形式化表示为∏＝（T，R，F，Comu，Secu，f）。

4 基于变邻域粒子群算法的调度策略

4.1 标准的粒子群优化算法

粒子群优化算法PSO（Particle Swarm Optimization），最早是由Kennedy J等人［9］于1995年提出的，是通过对鸟群捕食行为的研究，抽象出的一种基于迭代的优化算法。算法首先随机地初始化一个包含一定数量粒子的种群，种群中的每个粒子都代表一个潜在的解，粒子在问题的解空间中移动以找到最优或足够好的解。

在D维空间中，第i个粒子的位置可表示为xi＝（xi1，xi2，…，xiD）T，其速 度可以 表示为vi＝（vi1，vi2，…，viD）T，用pbest表示粒子本身所找到的历史最优解，用gbest表示整个种群找到的历史最优解，每一次迭代中，粒子的速度和位置通过如下两个公式进行更新：

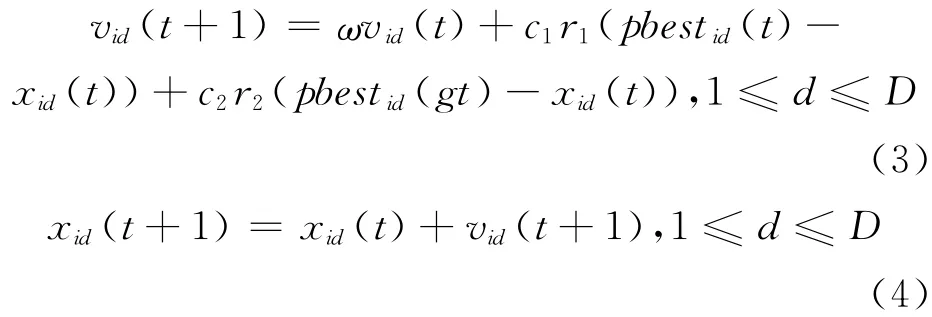
其中，ω称为惯性常量，用来限定当前速度对粒子飞行行为的影响；当ω取值较大时，算法具有较强的全局搜索能力；当ω取值较小时，算法具有较强的局部搜索能力。c1是正常量，用来限定个体经验对粒子飞行轨迹的影响。c2是正常量，用来限定群体经验对粒子飞行轨迹的影响。c1，c2被称为加速系数或学习因子，若c1＝0，则粒子只向群体学习，这样容易陷入局部极值；若c2＝0，则粒子只向自身学习，这样算法就退化为一个多起点的随机搜索，通常c1，c2在［0，4］上，一般取c1＝c2＝2。r1和e2是均匀分布在［0，1］区间的随机数，用以维护整个种群的多样性［10］。

每一维的粒子速度都被限定在最大速度Vmax内，每一维的粒子位置都被限定在最大边界B内。即：

并且

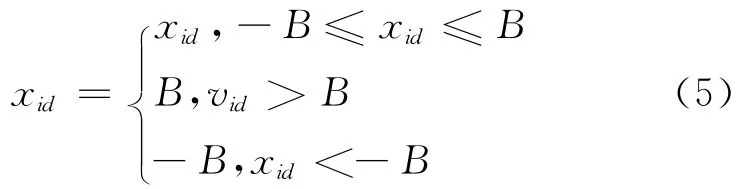
Vmax通常由β×B求得，其中0.1≤β≤1.0，并且通常情况下取β＝1。

PSO算法流程如图2所示。

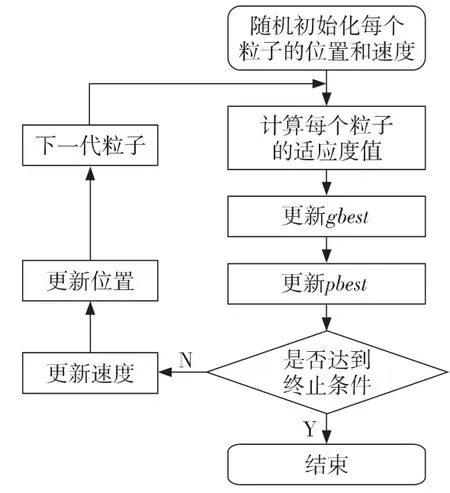
Figure 2 PSO flow diagram图2 PSO算法流程图

PSO算法的终止条件通常有三类［9］：

（1）达到最大迭代次数；

（2）在给定的迭代次数内结果没有提升；

（3）目标函数与最优值之间的误差小于预设值。

4.2 变近邻粒子群优化算法

变近邻搜索VNS（Variable Neighborhood Search）［11］是一种后启发式或构建启发式框架，旨在解决组合优化问题和全局优化问题。VNS通过反复探索不断扩大规模的邻域，并使用抖动策略，以寻求更好的局部最优解。VNS通过从gbest的邻域中抽取的起始点开始启动局部搜索，通过迭代地增加邻域的规模直到找到一个比当前值更好的局部最小值gbest，来逃离当前的局部最小值，重复这一步，直到达到预设的终止条件。变近邻粒子群优化算法VNPSO（Variable Neighborhood Particle Swarm Optimization）就是受VNS启发而来的。在粒子群算法中，当一个粒子的速度低于给定的阈值vc时，新的速度由式（6）和式（7）得到［12］：

其中，u是一个取值在［－1，1］中、服从均匀分布的随机数，即u～U（－1，1）。

根据粒子群优化算法中速度的特性可知：

（1）当vid＞0且｜vid｜较大的时候，意味着粒子在该维度更倾向于向着该方向飞行，即最优解在该速度的方向上；

（2）当vid＜0且｜vid｜较大的时候，意味着粒子在该维度更倾向于向着远离该方向飞行，即最优解在远离该维度的方向上；

（3）当｜vid｜处于0附近时，说明该维度的局部最优解就在粒子当前所在位置附近。

式（7）的目的就是在粒子速度很小的时候，添加一个随机扰动，让粒子不再围绕着当前的局部最优解来搜索，而是跳出该邻域结构，在另外一个区域开始新的搜索。

算法的性能直接由vc和φ决定，当vc取值较大时，可以减少摆动的周期，但是在同等条件下会增加粒子跳过局部最小值的概率，即大的vc迫使粒子保持较快的飞行状态，使其不能收敛到一个解上。φ的值直接影响粒子搜索的可变邻域。VNPSO算法如下所示：

算法 VNPSO

输入：算法所需的相关参数和结束条件。

输出：全局最优位置gbest。

步骤1 初始化粒子群规模N和其他相关参数；

步骤2 随机初始化每个粒子的位置和速度；

步骤3 把结果没有提高的迭代标志变量置0，flag＝0；

步骤4 while没有达到结束条件时do：

步骤5t＝t＋1；

步骤6 计算每一个粒子的适应度值；

步骤7 更新gbest为其历史最佳位置和当前所有粒子中使适应度值最小的位置；

步骤8 ifgbest得到改进thenflag＝0；

步骤9 elseflag＝flag＋1；

步骤10 fori＝1toN

步骤11 更新pbesti为其历史最佳位置和当

前位置中使适应度最小的位置；

步骤12 forj＝1toN

步骤13 ifflag＜10then

步骤14 使用式（3）～式（5）更新粒子第j维的速度和位置；

步骤15 else

步骤16 使用式（6）、式（7）、式（5）更新粒子第j维的速度和位置；

步骤17 nextj

步骤18 nexti

步骤19 end while

4.3 基于VNPSO算法的求解策略

为了在调度问题中使用PSO算法，最关键的是要把调度问题的解映射到粒子空间中。

对于本文讨论的含有m个原子操作的计算任务T＝｛O1，O2，…，Om｝和含有n个虚拟机的计算资源R＝｛vm1，vm2，…，vmn｝的问题，我们可以将它的一个可能的调度结果表示成矩阵x＝［xij］，其中i∈｛1，2，…，m｝，j∈｛1，2，…，n｝，当把操作Oi分配到虚拟机vmj上时，令xij＝1，否则令xij＝0。根据假设条件，一个操作只能分配到一台虚拟机上，则矩阵x＝［xij］的每一行的元素中有且仅有一个元素值为1，其余元素值为0。同理，可以把每个粒子的速度表示为矩阵v＝［vij］，其中vij∈［－1，1］。

可见，在这样的定义下粒子的位置是一个离散型的变量，并不能直接使用PSO算法。因此，我们需要对位置更新公式即公式（3）进行改造。考虑速度矩阵中的元素vij，当vij较大时，表示粒子在该维度更趋向于向该方向飞行；而位置矩阵中的对应元素xij表示操作Oi分配到虚拟机上，由于一个操作只能分配到一台虚拟机上，即每一行的元素中有且仅有一个元素值为1，则当位置矩阵第i行中第j列速度vij较大时，表示操作Oi更趋向于分配到虚拟机vmj上，那么在更新位置矩阵时可以将该粒子速度矩阵中每一行的最大值对应的元素在位置矩阵中置1，其他值置0：

每一个位置矩阵表示一个潜在的调度结果，而这个结果直接应用的话有可能会与工作流约束冲突，因此在算法开始前，对工作流约束中的操作进行拓扑排序，保证前驱操作都排在后继操作之前，并且在计算适应度函数时引入等待机制，以满足工作流约束的要求。如前文所示的工作流矩阵就是按拓扑排序后的操作生成的。

5 实验结果与分析

本文的实验使用的是云模拟平台Cloud－Sim［13］，版本号为3.0.2。CloudSim是澳大利亚墨尔本大学的网格实验室和Gridbus项目组推出的云计算仿真软件，它实现了云计算区别于其他分布式系统的主要特征，即将各类异构的计算资源虚拟化为资源池，屏蔽了物理层的部署细节，特别是其中的NetworkCloudSim组件，使其对应用程序中消息的传递和工作流约束等拥有良好的仿真能力，并能够更准确地评估资源调度和配置策略。

对图1所示的工作流任务，其相关参数的取值如下：

任务中每个操作的长度随机生成，取值范围为［100，500］，满足均匀分布，本次实验中操作长度取值如下，单位是MI：

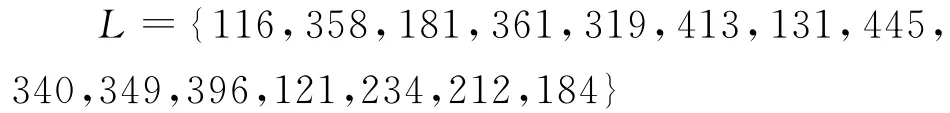
计算资源中虚拟机个数为4，计算能力取值为P＝｛4，6，8，10｝，单位是MIPS。虚拟机之间的通信矩阵如下所示，单位为ms（millisecond）：

对图1所示的工作流任务，其工作流矩阵如前文所示。

对于操作的安全需求，令第六个操作的安全等级需求为4，其余操作均为2，即sd6＝4。对于虚拟机的安全等级取值为SR＝｛2，2，3，4｝。对于安全约束，本次实验取最大风险跨度θ＝1，最大风险概率r＝0.2，即Secu＝（1，0.2），并且式（1）中的风险常数μ＝2。

VNPSO算法的相关参数取值如下：种群规模N＝30，加速系数c1＝c2＝1.4，最大速度Vmax＝1，对于惯性常数ω，采用常用的线性调整策略：

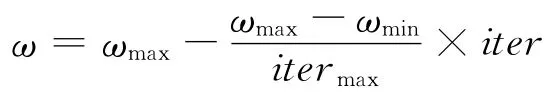
其中，ωmax、ωmin分别为ω的最大值和最小值，iter和itermax分别为当前迭代次数和最大迭代次数。本文的实验取ωmax＝0.9，ωmin＝0.4，即随着迭代的进行，ω由0.9线性递减到0.4。

对于式（7）中的参数φ和vc，其取值在前3／4的迭代中取2和0.001，在剩下的迭代中取5和1e－5。

本文中与VNPSO算法做对比的是Max－Min蚁群算法MMACO（Max－Min Ant Colony Optimization）［14］和 遗 传 算 法GA（Genetic Algorithm）［15］。

MMACO算法的相关参数为：蚁群规模为30，信息启发式因子和期望启发式因子均取1，信息素挥发系数取0.2，最佳解概率取0.005。GA算法的相关参数为：种群规模为30，交叉算子取0.8，变异算子取0.1

三个算法的终止条件均为迭代1 000次后终止。

实验中，三个算法的种群规模相同，都是30，因此这三个算法的收敛速度都取决于种群对问题空间的搜索能力。

由式（3）可以看出，在PSO算法中，粒子的速度受两大因素的影响：首先，在惯性常量ω的作用下，沿着原速度方向对问题空间进行搜索，ω的大小就决定了粒子沿着原速度方向运动的步长，所以当ω越大，该粒子对问题空间搜索的速度就越快；其次，在pbest和gbest的共同影响下，粒子会对速度的方向进行调整，逐渐向最优解的方向进行搜索；最后，由随机数r1和r2保证了粒子种群的多样性。通过分析可以看出，由于每次迭代时种群绝大部分的粒子都会向着最优解的方向对自身位置进行调整，因此每次迭代后，PSO算法都能对问题空间中更多潜在解进行搜索，所以PSO算法具有很好的全局搜索能力。

在ACO算法中，由于初始状态下各个节点的信息素含量相同，均为初始值，此时蚁群中的每只蚂蚁都会随机地选取前进的路径；随着迭代次数的增加，每只蚂蚁在选择前进路径的时候，会依信息素分布的强弱，依概率选择较好的路径，这样一方面使寻找的路径逐渐向目前发现的最优路径上靠拢，另一方面这种依概率的选择也保证了蚁群的多样性。特别是在Max－Min蚁群算法中，只有迭代最优的蚂蚁或全局最优的蚂蚁会对信息素进行更新，这样就更加保证了算法对问题空间的的全局搜索能力。因此，蚁群算法在前期会有一个较为平缓的收敛过程，但随着迭代的进行，信息素逐渐积累起来，算法会迅速向最优解的方向收敛。

在GA算法中，由于对种群的更新的主要操作是交叉和变异，而变异操作概率较低，交叉操作在上一步选取的编码相对优秀的基因中随机配对进行，所以每次迭代后对种群中产生的新的个体数量与前两种算法相比所占比例较小，并且多样性与前两种算法相比略显不足，因此相对而言，GA算法需要较多的迭代次数后才能达到与前两种算法相同的结果。

在如前所给定的相关参数下，三个算法随迭代次数的增加，其收敛情况如图3所示。由于这三个算法的初始种群都是随机生成的，故初始种群的质量对算法的收敛有很大的影响。图3中的数据是经过多次独立实验后，选取的一组有相近起始时间的数据进行的对比。

Figure 3 VNPSO，MMACO，GA convergence curves图3 VNPSO、MMACO、GA算法收敛曲线

从图3中可以看出，VNPSO算法由于起始时惯性常量设置较大，因此具有较强的全局搜索能力，故前期搜索收敛速度很快，但由于PSO算法的特性，当到达一个极值点后很难脱离，这时VNS策略的引入，让算法能够在极值点周围震荡，使搜索能够继续进行，让算法逐渐向最优解靠近；对于MMACO算法，由于迭代起始阶段信息素较少，故算法收敛速度较慢，但随着算法的进行，ACO算法良好的寻优能力逐渐显现出来，使算法逐渐向最优解靠近；由于GA算法的全局搜索对交叉操作和变异操作依赖较大，故其全局搜索速度较其他两个算法略显不足。

对三个算法在有安全约束和无安全约束的条件下分别进行10次独立实验。图4所示为有安全约束的条件下，每个算法在首次取得低于250ms的解时所需要的迭代次数，其中，VNPSO平均需要223次，MMACO平均需要348次，GA算法平均需要598次。

Figure 4 Iteration times of each algorithm’s makespan first reaching 250ms图4 首次取得低于250ms的解时所需要的迭代次数

可以看出，三个算法中VNPSO算法具有较高的收敛速度。10次独立实验中，每个算法在经过1 000次迭代后所求得的完成时间的平均值如图5所示。

Figure 5 Average makespan of each algorithms图5 VNPSO、MMACO、GA算法平均完成时间对比

可以看出，由于本实验的安全约束较为宽松，故安全约束对平均完成时间的影响并不大。

在此基础上，本文对200个操作20台虚拟机的情况做了进一步的实验。对安全约束做如下定义：从200个操作中随机抽取20个并把它们的安全需求设置为4，其他操作安全需求设置为2；从20台虚拟机中随机抽取4台并把它们的安全等级设置为4，再随机抽取4台并把它们的安全等级设置为3，其余设置为2。实验取最大风险跨度θ＝2，最大风险概率r＝0.2，即Secu＝（2，0.2），并且式（1）中的风险常数μ＝3。实验结果如图6所示。

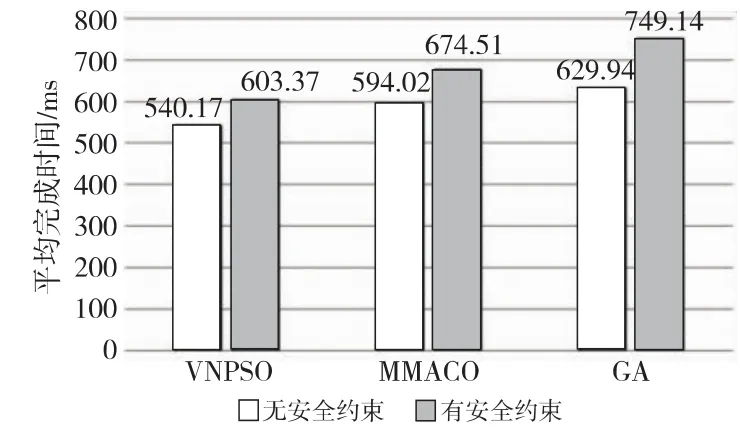
Figure 6 Experience with 200operations and 20virtual machines图6 200个操作20台虚拟机下的对比

6 结束语

本文对云环境下工作流任务的资源调度问题进行了建模，在此基础上给出了一个安全约束模型，并使用VNPSO算法对问题进行了求解。同时，在Cloudsim仿真平台下，把VNPSO算法与常用的智能优化算法进行了对比。实验表明，VNPSO算法是有效的，并且由于在全局搜索和局部搜索之间进行了良好的平衡，使得该算法具有很好的寻优能力。

［1］ Mell P，Grance T.The NIST definition of cloud computing（draft）［S］.NIST Special Publication 800－145，2011.

［2］ Abrishami S，Naghibzadeh M，Epema D H J.Deadline－constrained workflow scheduling algorithms for infrastructure as a service clouds［J］.Future Generation Computer Systems，2013，29（1）：158－169.

［3］ Liu K，Jin H，Chen J，et al.A compromised－time－cost scheduling algorithm in swindew－c for instance－intensive cost－constrained workflows on a cloud computing platform［J］.International Journal of High Performance Computing Applications，2010，24（4）：445－456.

［4］ Rao J，Wei Y，Gong J，et al.QoS guarantees and service differentiation for dynamic cloud applications［J］.IEEE Transactions on Network and Service Management，2013，10（1）：43－55.

［5］ Wu Z，Liu X，Ni Z，et al.A market－oriented hierarchical scheduling strategy in cloud workflow systems［J］.The Journal of Supercomputing，2013，63（1）：256－293.

［6］ Ergu D，Kou G，Peng Y，et al.The analytic hierarchy process：Task scheduling and resource allocation in cloud computing environment［J］.The Journal of Supercomputing，2013，64（3）：1－14.

［7］ Hamlen K，Kantarcioglu M，Khan L，et al.Security issues for cloud computing［J］.International Journal of Information Security and Privacy（IJISP），2010，4（2）：36－48.

［8］ Song S，Hwang K，Kwok Y K.Risk－resilient heuristics and genetic algorithms for security－assured grid job scheduling［J］.IEEE Transactions on Computers，2006，55（6）：703－719.

［9］ Kennedy J，Eberhart R.Particle swarm optimization［C］∥Proc of IEEE International Conference on Neural Networks，1995：1942－1948.

［10］ Shi Y，Eberhart R C.Parameter selection in particle swarm optimization［C］∥Proc of the 7th International Conference on Evolutionary Programming VII，1998：591－600.

［11］ Hansen P，Mladenovic N.Variable neighborhood search：Principles and applications［J］.European Journal of Operational Research，2001，130（3）：449－467.

［12］ Liu H，Abraham A，Choi O，et al.Variable neighborhood particle swarm optimization for multi－objective flexible jobshop scheduling problems［C］∥Proc of the 6th International Conference on Simulated Evolution and Learning，2006：197－204.

［13］ Garg S K，Buyya R.NetworkCloudSim：Modelling parallel applications in cloud simulations［C］∥Proc of the 4th IEEE International Conference on Utility and Cloud Computing（UCC），2011：105－113.

［14］ Pitakaso R，Almeder C，Doerner K F，et al.A MAX－MIN ant system for unconstrained multi－level lot－sizing problems［J］.Computers ＆Operations Research，2007，34（9）：2533－2552.

［15］ Omara F A，Arafa M M.Genetic algorithms for task scheduling problem［J］.Journal of Parallel and Distributed Computing，2010，70（1）：13－22.