不同博弈框架下的双渠道供应链联盟模式选择

浦徐进， 诸葛瑞杰， 曹文彬

（江南大学 商学院，江苏 无锡 214122）

供应链联盟是节点企业为最大程度增进收益所采取的一种组织形式，从目前的发展趋势看，供应链联盟正在逐步取代企业集团的位置，被视为未来企业组织形式发展演变的主流趋向。如IBM、思科（Cisco）、戴尔（Dell）、沃尔玛、丰田、尼桑和耐克等世界知名的大企业，通过构建灵活和有效的供应链联盟，极大地巩固或确立了自己的领导地位。

根据联盟双方所从事的活动性质，战略联盟可以分为纵向联盟和横向联盟2种主要模式。纵向联盟是指处于供应链上、下游有关系的企业之间建立的联盟，这种战略联盟的关键是供应链不同环节的企业基于自身的核心竞争能力，采取专业化的分工与合作实现最大程度的增值；横向联盟是竞争对手之间的联盟，由于合作各方在连续不断的基础上共同从事一项活动，从而改变了一项活动的进行方式。目前，横向联盟主要包括R＆D方面的联盟、生产阶段的联盟和销售阶段的联盟等形式。

由于联盟的建立有利于各企业成员和供应链竞争力的提升，实现供应链整体绩效的提高，因此，如何构建适宜的供应链战略联盟模式，一直是供应链管理研究领域的热点之一。

供应链联盟关注构建长期的战略协作关系，强调相互之间的信任与合作。近年来，国外学者针对供应链联盟的治理机制、影响因素及可持续发展路径等问题开展了大量研究。文献［1］研究了供应链联盟中的利润分配与联盟稳定性之间的关系；文献［2］着眼于分析供应链联盟契约治理机制，对比了不同契约形式对供应链联盟合作绩效的影响；文献［3］研究了供应链中纵向整合趋势因素以及对于制造商下游的整合结果；文献［4］基于资源基础、权变和社会交换理论，通过实证调查和测试框架，研究了联盟动机、环境、资产专用性、伙伴间相互依存关系和关系资本因素对制造业战略联盟结果的影响；文献［5］通过构建一个博弈论模型，研究弱零售商从制造商主导的零售商联盟中的获利情况，研究表明，当2个零售商在价格方面竞争不强时，有利于联盟整体的形成；而当在价格和服务方面出现分化时，对联盟中所有成员都有利；弱零售商在联盟中获得收益与否取决于相互作用中溢出服务效果；文献［6］在供应链联盟背景下，基于资源依赖、社会网络和应急理论，提出了一个将联盟可持续发展性与供应链内外部环境联系起来的模型，最后用罗尔斯·罗伊斯公司和空中客车公司的伙伴关系在航空业演变的案例，证实模型的正确性。

外部市场环境的变化，使我国企业也开始逐步意识到开展供应链战略合作的重要性及其潜在效益。因此，国內研究者在分析影响供应链联盟因素的基础上，结合我国实际情况，提出了国内企业发展供应链联盟的策略。文献［7］通过对攀钢钒钛产业链的研究，认为供应链联盟必须从资源驱动型向资本与知识驱动型转变；文献［8］基于供应链联盟伙伴企业之间合作竞争关系建立了Volterra模型，讨论了合作竞争下均衡解的存在及均衡条件；文献［9］针对制造企业与物流企业组成的共生系统，研究共生联盟形成前后能量的变化，研究表明：在共生联盟形成后，物流企业获得的利润分配参数较小，但共生系统和共生单元的能量增加较多，物流企业的总能量增大；文献［10］针对存在1个上游供应商和1个下游制造商的2层供应链，分析比较了当下游企业进行技术创新时，上、下游企业非合作创新和合作创新博弈形式下各企业的选择策略及利润函数，研究结果表明，合作创新是一种双赢的策略，制造商与供应商都能获得比非合作情况下更多的利润，同时供应链系统达到有效帕累托最优。

本文重点研究在不同的博弈框架下，不同供应链成员将偏好于何种联盟模式，是否存在实现供应链整体利润最大化的协调机制，这一协调机制能否保证供应链整体联盟的稳定性，以及如何设计这一协调机制。

1 非合作博弈框架下的模型构建

模型构建是基于单一供应商S和2个零售商R1、R2组成的2层供应链，其中供应商和零售商都是风险中性的理性决策主体。供应商提供产品的单位成本为c，供应商同时向2个零售商提供产品，产品的批发价格为w。零售商向消费者出售产品，pi为零售商i的零售价格（i＝1，2），QRi为零售商i的销售量。参考文献［11－13］，将零售商销售量函数形式定义为：

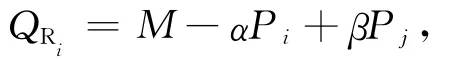
其中，j＝3－i；M 为市场总需求量；α为价格敏感系数，表示市场需求对自身零售价格变动的反应程度或敏感程度；β为零售商间的敏感系数，反映一方市场价格变化时对另一方市场需求的影响。

为了保证研究具有实际意义，假设α＞β＞0，M＞αpi，t＝（α／β）＞1。可确定产品不存在滞销，即D＝QS＝QR1＋QR2。

基于上述假设，本文首先在非合作博弈框架下构建4种供应链联盟模式，即整体联盟、个体分散决策、“零售商＋零售商”横向联盟、“供应商＋零售店”纵向联盟，对比分析不同联盟模式下供应商和零售商间的博弈结果。

1.1 整体联盟模式

供应商和2个零售商组建整体联盟进行联合决策，供应链整体的利润函数为：

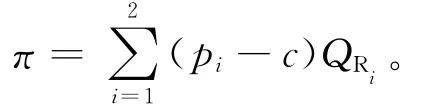
将QR1、QR2代入π，同时对π分别求关于p1、p2的偏导数，并令其等于0，可得：

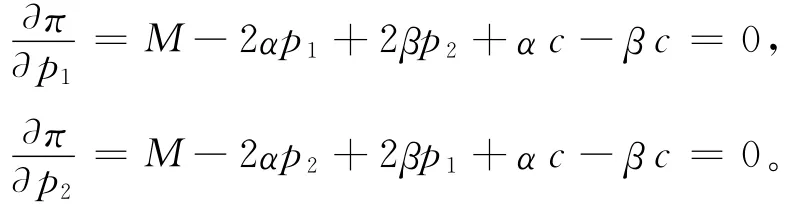
联立上述2个方程，容易得到此时零售商最优零售价格p1、p2为：

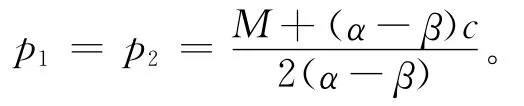
从而可以得到零售商最优销售量QR1、QR2及供应链整体利润π分别为：

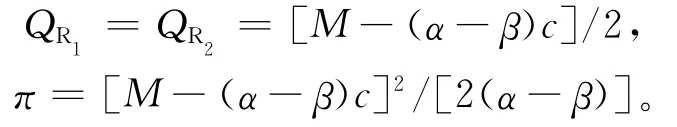
1.2 个体分散决策模式

事实上，当供应商和2个零售商均为分散独立的决策者时，三者中是不存在联盟整合的，为了对比需要，将这种情况也认为是联盟模式的一种。供应商先确定批发价格w′，2个零售商根据w′结合自身利益最大化要求，确定产品的最优零售价pi′和订货量QRi′。所以，2个零售商在零售市场上进行Betrand博弈，而供应商和零售商之间进行Stackelberg博弈。利用逆推归纳法求解如下博弈模型：

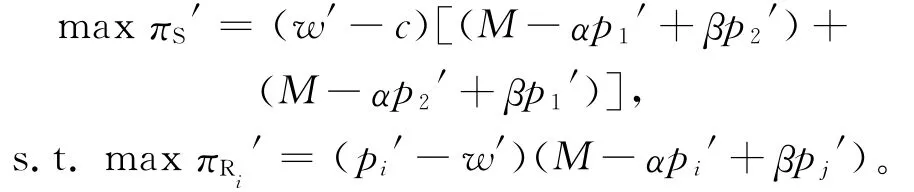
与前文的计算过程类似，同理可以得到此时供应商最优批发价格w′、零售商最优零售价格p1′和p2′、零售商最优销售量QR1′和QR2′、零售商利润πR1′和πR2′、供应商利润πS′和供应链整体利润π′分别为：

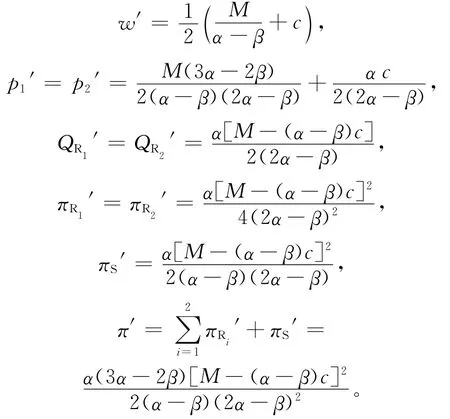
1.3 “零售商＋零售商”横向联盟模式

为了谋取更大的利益，2个零售商可能联合起来对抗供应商。2个零售商组成横向联盟，供应商确定批发价格w″，零售商联盟根据w″确定联盟利润最大化的最优零售价格pi″和订货量QRi″。供应商和零售商联盟之间进行Stackelberg博弈，利用逆推归纳法求解如下模型：

同理可以得到此时供应商最优批发价格w″、零售商最优零售价格p1″和p2″、零售商最优销售量QR1″和QR2″、零售商利润πR1″和πR2″、供应商利润πM″和供应链整体利润π″分别为：

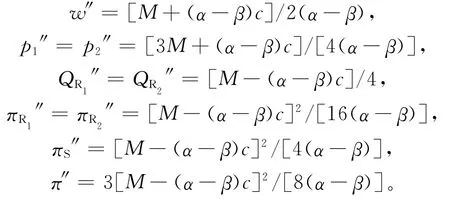
1.4 “供应商＋零售店”纵向联盟模式

在供应商和零售商i组成联盟的情形下，供应商确定给予零售商j的批发价格w‴、零售商Ri的零售价格pi‴和订货量QRi‴，零售商Rj根据批发价格w‴确定自己产品的零售价格pj‴和订货量QRj‴（j＝3－i）。供应商和零售商i组成的联盟和零售商j之间进行Betrand博弈，利用逆推归纳法求解如下博弈模型：

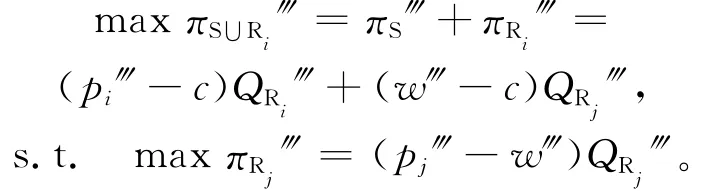
同理可以得到此时供应商最优批发价格w‴、零售商最优零售价格pi‴和pj‴、零售商最优销售量QRi‴和QRj‴、零售商利润πRi‴和πRj‴、供应商利润πM‴和供应链整体利润π‴分别为：

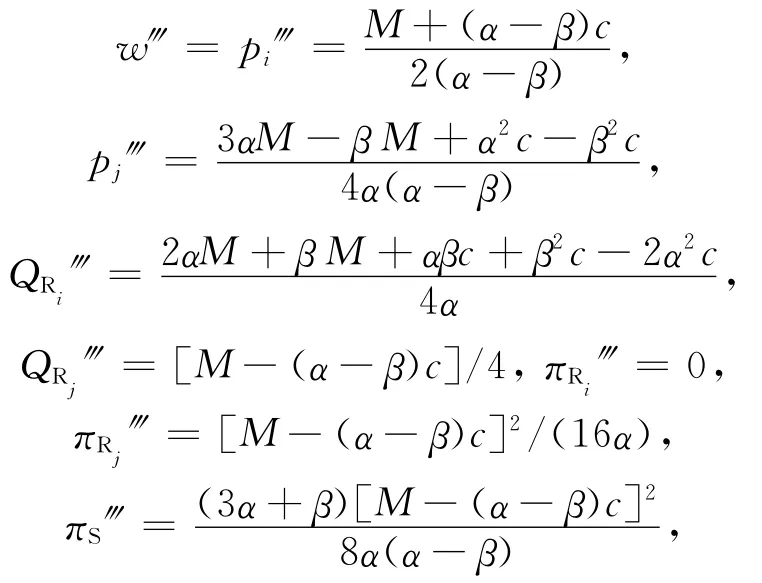
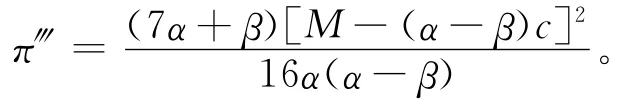
1.5 4种模式的结果对比

（1）比较整体联盟和个体分散决策2种模式下零售商价格和销售量，可以发现：

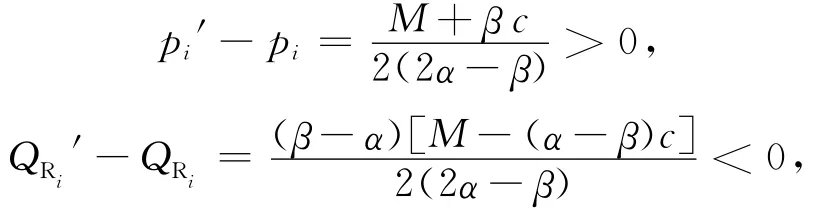
即i＜pi′，QRi＞QRi′，由此可得以下命题1。

命题1 与个体分散决策模式相比，整体联盟模式下的零售商价格会降低，而零售商销售量都会增加。

（2）比较4种模式下零售商、供应商以及供应链整体利润的变化，可以发现：

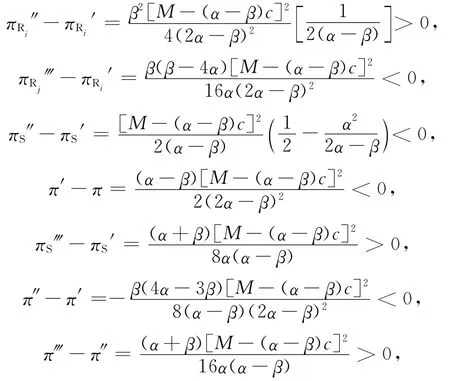
由此可得以下命题。

命题2 在“零售商＋零售商”横向联盟模式下，零售商利润最大；在“供应商＋零售店”纵向联盟模式下，零售商利润最小。值得注意的是，在“供应商＋零售店”纵向联盟模式中，参与联盟零售商的利润为0，而独立零售商的利润虽然大于0，但都小于其他模式下的利润。

命题3 在“供应商＋零售店”纵向联盟模式下，供应商利润最大；在“零售商＋零售商”横向联盟模式下，供应商利润最小。

命题4 在整体联盟模式下，供应链整体利润最大；在“零售商＋零售商”横向联盟模式下，供应链整体利润最小。

综合上述分析，发现在非合作博弈框架下，理性的供应链成员（供应商、零售商）偏好于不同的联盟模式，零售商偏好于“零售商＋零售商”横向联盟模式，供应商偏好于“供应商＋零售店”纵向联盟模式；供应链成员追求自身利润最大化的行为与整体联盟模式的运作目标相冲突，从而不能实现供应链整体利润最优化。因此，本文将通过Shapley值法设计利润分配方案，寻找在满足一定条件时，整体联盟在合作博弈框架下实现稳定合作的可能性。

2 合作博弈框架下的模型构建

Shapley值法是解决N人合作对策问题的一种合作博弈形式，其核心思想是基于参与各方的边际贡献，设计一种公平的利益分配方案以维持联盟运作的稳定性。

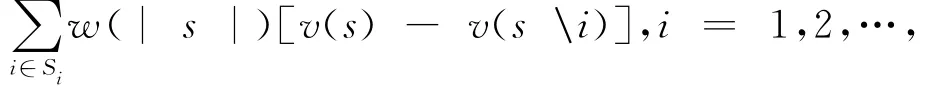
其中，Si为集合I中包含成员i的所有子集；｜s｜为子集s中的元素个数；w（｜s｜）为加权因子；v（s）为子集s的效益；v（s＼i）为子集s中除去成员i后可取得的效益［14］。

利润分配方案不仅要从整体出发，而且还要考虑到局部合理，只有这样，成员之间的合作才能稳定。

2.1 满足合理分配方案条件

与文献［14－17］的分析方法一致，容易验证，一个合理的分配方案必须满足3个条件。

（1）个体合理性。Φi（v）≥v（i），i＝1，2，…，n，如果成员单独干时获得的利润比在合作时所分的利润多，则它就有了单方面离开合作的动机。

通过分析，各种供应链联盟模式下，供应商和零售商的利润见表1所列。

基于Shapley值法的理论模型，可以计算得到合作博弈框架下各参数的具体表达式，结果见表2所列。

表1 各种供应链联盟模式下供应商和零售商的利润

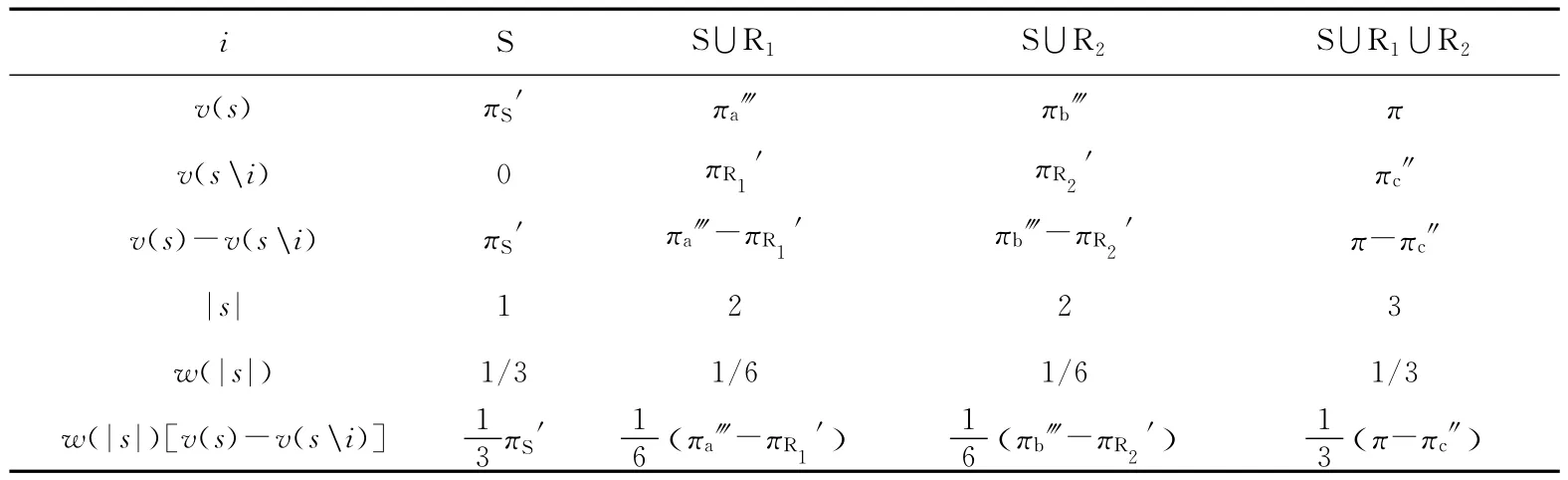
表2 Shapley值法中的各参数具体表达式

供应商的利润分配额ΦS（v）为：

零售商Ri的利润分配额ΦRi（v）为：

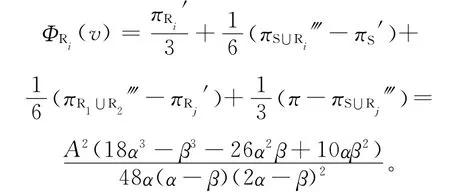
2.2 考察分配方案合理性

（1）满足个体合理性要求，必须有：

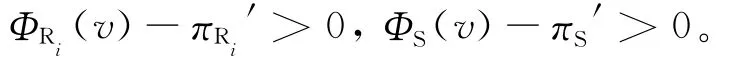
若需ΦRi（v）－πRi′＞0，则由ΦRi（v）和πRi′，必须有：

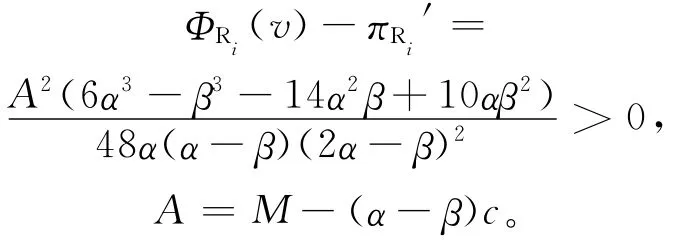
因为t＝（α／β）＞1，因此上述不等式成立，即满足：

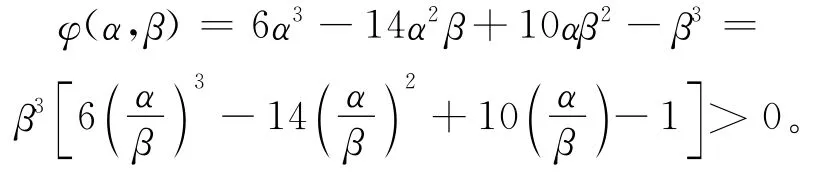
令t＝α／β，只需φ（t）＝6t3－14t2＋10t－1＞0，分析φ（t）发现，φ（t）在［1，＋∞）上单调递增。又因为t＝（α／β）＞1，所以φ（t）仅在［1，＋∞）上有意义，而φ（1）＝1＞0，可以证明ΦRi（v）－πRi′在［1，＋∞）上始终大于0。

若需ΦS（v）－πS′＞0，则由ΦS（v）和πS′的表达式，必须有：

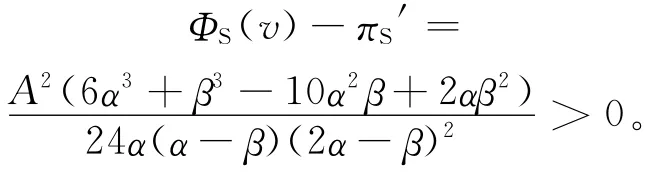
同理可得上述不等式成立，即满足：

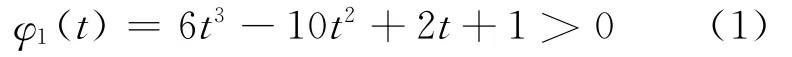
（2）容易证明得到，π＝ΦS（v）＋ΦR1（v）＋ΦR2（v）＝A2／2（α－β），则整体合理性必然满足。

（3）满足特殊独立合理性，必须有：

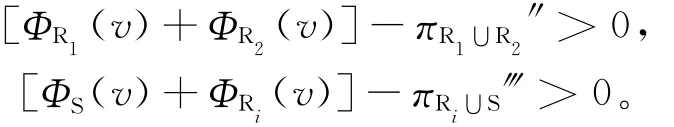
若需［ΦR1（v）＋ΦR2（v）］－πR1∪R2″＞0，则有：

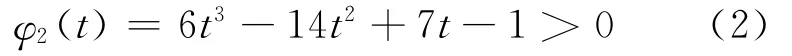
若需［ΦS（v）＋ΦRi（v）］－πRi∪S‴＞0，则有：

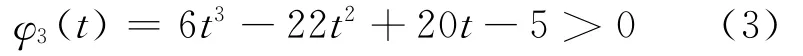
将φ1（t）、φ2（t）、φ3（t）的关系绘制成图1所示形式，它们分别与t轴相交的点为t1、t2、t3。

由图1发现，基于Shapley值法设计的利润分配机制，t可以取大于1的任意值，整体合理性条件一直都能满足。但是，另外2个条件的满足与否与t的取值有关。当1＜t≤t1时，个体合理性和特殊独立合理性均不能得到满足；当t1＜t≤t2时，横向和纵向联盟情形下的特殊独立合理性不能得到满足，但个体合理性能得到满足；当t2＜t≤t3时，纵向联盟情形下的特殊独立合理性不能得到满足，但横向联盟情形下的特殊独立合理性和个体合理性能得到满足；当t＞t3时，才能同时满足个体合理性和特殊独立合理性。因此，可以得到命题5。

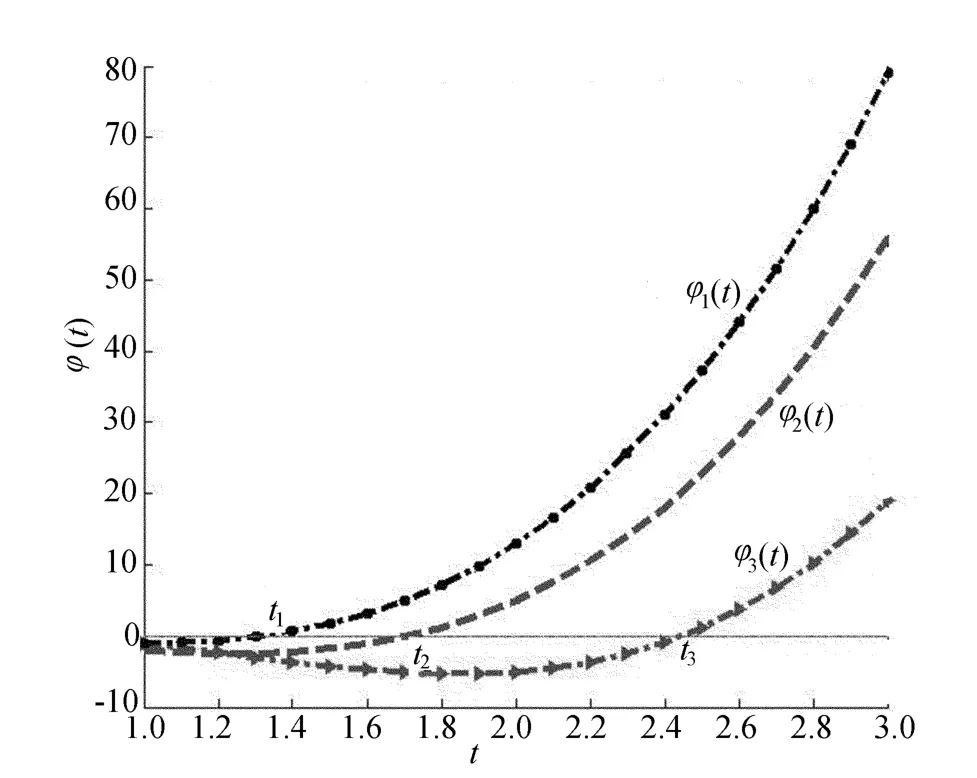
图1 φ1（t）、φ2（t）、φ3（t）的关系

命题5 只有当价格敏感系数与零售商间敏感系数的比值超过一个临界值时，基于Shapley值法设计的利润分配机制才能保证供应链整体联盟模式实现稳定合作。

综合上述分析，可以发现在合作博弈框架下，通过Shapley值法设计的供应链整体联盟利润分配方案，不仅能够保证供应链整体实现利润最大化，而且也能使供应链成员（供应商、零售商）的收益，比在非合作博弈框架下得到Pareto改进。因此，这一利润分配方案能够成为保障供应链整体联盟稳定运作的合作机制。

3 结束语

作为供应链企业合作关系的最高形式，供应链联盟打破了现存价值链的结构，能够保证企业达到共赢的协同效应，因而正在成为企业之间、供应链之间竞争的最新手段。本文研究发现，在非合作博弈框架下，供应商和零售商各自偏好于不同的联盟模式，供应链整体利润不能实现最大化；在合作博弈框架下，当价格敏感系数与零售商间敏感系数的比值满足一定条件时，基于Shapley值法设计的利润分配方案是保障自愿合作、实现供应链整体利润最大化的有效途径。

［1］Mahesh N，Greys S.Game－theoretic analysis of cooperation among supply chain agents：Review and extensions［J］.European Journal of Operational Research，2008，187（3）：719－745.

［2］Hennet J C，Arda Y.Supply chain coordination：agametheory approach［J］.Engineering Applications of Artificial Intelligence，2008，21（3）：399－405.

［3］Guan Wei，Rehme J.Vertical integration in supply chains：driving forces and consequences for a manufacturer’s downstream integration［J］.Supply Chain Management：An International Journal，2012，17（2）：187—201.

［4］Sambasivan M，Loke S P，Mohamed Z A，et al.Factors influencing strategic alliance outcomes in a manufacturing supply chain：role of alliance motives，interdependence，asset specificity and relational capital［J］.Int J Production E－conomics，2013，141：339－351.

［5］Amrouche N，Yan Ruiliang.Can a weak retailer benefit from manufacturer－dominant retailer alliance？［J］.Journal of Retailing and Consumer Services，2013，20：34－42.

［6］Shymko Y，Diaz A.A resource dependence，social network and contingency model of sustainability in supply chain alliances［J］.Int J Business Excellence，2012，5：502－519.

［7］程宏伟，冯茜颖，张永海.资本与知识驱动的产业链整合研究：以攀钢钒钛产业链为例［J］.中国工业经济，2008（3）：143－151.

［8］卓翔芝，王 旭，王振锋.基于Volterra模型的供应链联盟伙伴企业合作竞争关系研究［J］.管理工程学报，2010，24（1）：134－137.

［9］王笃鹏，王 虹，周 晶.共生联盟模式下制造企业与物流企业均衡利润分配研究 ［J］.管理学报，2010，7（8）：1228－1232.

［10］刘志迎，李芹芹.产业链上下游链合创新联盟的博弈分析［J］.科学学与科学技术管理，2012，33（6）：36－40.

［11］Zhang Weiguo，Fu Junhui，Li Hongyi，et al.Coordination of supply chain with a revenue－sharing contract under demand disruptions when retailers compete［J］.Int J Production Economics，2012，138：68－75.

［12］易余胤.不同主导力量下的闭环供应链模型［J］.系统管理学报，2010，19（4）：389－396.

［13］韩敬稳，赵道致.力量不对等供应链下游寡头行为演化机理［J］.北京理工大学学报：社会科学版，2012，14（2）：51－57.

［14］胡盛强，张毕西，关迎莹.基于Shapley值法的四级供应链利润分配［J］.系统工程，2009，27（9）：49－54.

［15］公彦德，李帮义，刘 涛.基于Shapley值和相同利润增长率的供应链协调策略［J］.系统管理学报，2009，18（1）：61－66.

［16］张成堂，武 东，周永务.联盟博弈下基于Shapley值法的三层供应链协调机制［J］.工程数学学报，2011，28（6）：763－770.

［17］刘 勇，周永务.一类基于价格的随机需求条件下供应链的订购与协调机制［J］.合肥工业大学学报：自然科学版，2009，32（10）：1627－1632.