基于准实时数据的智能配电网理论线损计算

李 滨，杜孟远，韦 维，韦 化

（广西大学 电气工程学院，广西 南宁 530004）

0 引言

智能电网利用现代通信手段和计算机技术实现发电与用电之间信息双向流动。得益于强大的信息采集、分析与控制能力，智能电网具有自我修复、自适应性强、安全可靠和经济高效等优势［1］。当前智能电网正朝着信息化、数字化、自动化和互动化方向发展［2］。

为了对智能电网运行情况进行监测，配电线路始端和变压器处都装有量测终端，每隔一定时间自动将测量数据传回供电局。对于配电网中的量测终端，当前技术难以保证较高的同步性，同一时刻传回的数据可能是不同时刻的测量值，只能称为准实时数据。这些数据分散存储于供电局的不同系统中，没有实现数据共享，缺乏有效利用的方法。

线损率是综合反映电网企业规划设计、电网建设、技术进步、生产运行和经营管理水平，衡量电网电能损耗高低的一项重要经济技术指标。配电网电压等级低，线路和变压器电量损失大，为了更好地进行线损管理，运行人员对其实时性或准实时性提出了更高的要求。

当前配电网理论线损计算可以分为传统方法和智能算法2类［3-7］。鉴于我国配电网实际情况，传统计算方法主要有等值电阻法、均方根电流法等方法。这些方法都是基于电流进行计算。传统计算方法采用的模型较简单，不依赖很详细的运行数据，适合手工计算。由于没有用到智能配电网中大量的量测数据，传统方法的计算结果精度不高，输出结果不够丰富，不能满足电力企业对线损管理的要求。随着智能电网技术的完善，配电网的线损计算可以采用的数据逐渐增多，研究利用智能终端的准实时数据精确评估线损情况，更好地指导降损工作，在理论与实践上都有重要意义。当前智能电网的建设还处于起步阶段，配电网自动化覆盖率低，可以采集的数据较少，甚至只能获得馈线始端电压、注入的电流和功率。供电局的不同系统中存有大量准实时数据的历史记录，有些系统能够提供实际的负荷曲线，若能加以有效利用，则可以在一定程度上弥补数据较少的不足。

本文提出一种准实时数据的配电网理论线损计算方法。利用线路始端节点注入功率和部分变压器量测终端的准实时功率，估计出与实际运行情况相符的配电网潮流状态进行线损计算。与基于电流法的理论线损计算方法不同的是，本文提出的方法以潮流作为状态估计结果，不仅可以得到每条支路的线损情况，还能比较精确地得到节点电压值，进而对电压质量进行评估。本文方法可以满足在线计算要求，其潮流结果可以作为降损优化计算的基础数据，为降损措施提供数据支持。

1 配电网理论线损计算的优化模型

1.1 状态估计

智能电网的监测与调度离不开状态估计。状态估计利用冗余的测量数据，获得最接近系统实际运行状态的估计值［8］。理论上当状态估计的结果与实际系统运行情况一致程度较高时，估计结果计算的线损也应该有较高的精度。然而配电网呈辐射状、分支多，从经济角度考虑难以像输电网一样在所有支路上安装量测装置，量测数据的冗余度较低，不能直接使用早已在输电网中广泛应用的状态估计方法。针对当前情况，很多学者提出了一些适用于智能配电网的状态估计方法［9-13］。目前大多数方法需要事先知道所有负荷的功率，难以应用到量测数据比较少的配电网上。

状态估计也称作滤波，目的是尽量从被噪声污染的数据中提取出系统实际值。假设电力系统的测量值用z表示，存在如下关系：

其中，xϵRl为状态量；h（x）ϵRm为与状态变量有关的函数；eϵRm为服从正态分布的量测误差。若以h（x）表示量测量的真实值，则式（1）具有明确的物理意义，即真实值在传输过程中受到其他因素的影响，各种误差叠加后得到测量值。状态估计中量测量多于状态量，因而可以利用多余的量测资源重复量测，提高状态量的估计精度。

1.2 智能配电网理论线损模型

相对基于电流法的方法而言，以潮流法为基础的理论线损计算可以提供较为精确的结果，同时也能提供较为丰富的结果信息。若能得到网架信息以及每个节点流入和流出功率的数据，便可以利用任意一种方法求解潮流方程，计算潮流状态和线损情况。受建设成本的限制，即使智能配电网也难以在线路的所有位置安装量测终端，且使用无线传输时易受外界影响，不能避免数据丢包现象，很多情况下无法获得每个节点的数据，量测量的冗余度比较低。现场传回的量测量是准实时值，传输过程中也会受到噪声的污染，直接应用会带来较大误差。基于潮流的状态估计可以尽可能消除噪声对测量值的影响，但在配电网量测量少于状态量时无能为力，更不能估计出没有量测量的状态量。为了利用潮流对配电网进行理论线损计算，本文提出了基于状态估计的智能配电网理论线损计算模型。

式（2）采用不带权系数的目标函数不但降低了模型的复杂程度，也利于现场应用。式（3）是包含配电网所有节点的潮流方程。与传统的状态估计中的等式约束是零注入方程不同，本文的等式约束是潮流方程。加入潮流方程有2个重要的作用：一是实际存在的配电网潮流状态必然满足潮流方程，加入这个约束可以提高状态估计的合理性与估计精度；二是利用潮流方程可以推算出缺失量测量节点的信息。和输电网测量设备众多不同，在配电网量测量冗余度比较低的情况下，很难用状态估计常用的最小二乘法估计出所有状态量，但状态量之间隐含着由潮流方程描述的电路理论上的联系。潮流方程是非线性的，难以显式地给出描述各量测量间联系的数学表达式，可作为等式约束利用迭代方法由一个状态量隐式地推出另一个状态量。

典型的状态估计是没有不等式约束的，但本文模型引入的不等式约束对于提高状态量估计的精度有着重要作用。一般而言，各节点电压都在额定电压附近，用式（4）进行约束。式（5）、（6）中上下限可以通过历史数据获得。某些节点量测值的误差会对另一些状态量产生影响，使得这些状态量的值偏离实际值较远。若没有不等式约束，则这些偏离实际值较远的状态量又会影响另一些节点状态量的估计，从而严重影响估计结果。不等式约束能够对可能偏离实际值较远的估计值进行限制，将其箝制在合理范围内，减少对其余节点的影响。

在不考虑其他电源的情况下，用潮流法进行配电网线损计算时只需要知道负荷节点功率和电压。为了简便，可以直接选择负荷功率作为量测量，即：

其中，PD0和QD0分别为负荷有功、无功的量测量。

选择量测函数等于负荷功率，即：

通常状态估计选择电压幅值和相角作为状态量，完成估计后利用这些量计算功率、电流等其他量。本文为了估计负荷和计算分支线路、变压器的功率损耗情况，选择

作为状态量，其中，α为节点电压相角，其余各变量的意义如前文所述。本文引入的潮流约束已经包含了负荷和电压之间的关系，与传统方法估计完成后再计算负荷是等价的。

式（2）—（6）是一个有等式和不等式约束的非线性优化问题。式（3）是网络潮流约束，式（4）—（6）与最优潮流中的安全运行约束一致，只是表达的意义不同，与最优潮流在形式上一致［14］。最优潮流的不等式安全约束是为了对系统进行控制，将运行状态限制在安全范围内。本文的不等式约束没有对系统进行控制的目的，只是为了限制错误数据对估计结果的影响。通常最优潮流以经济性作为目标，得到一种系统的调节方案供运行人员参考。本文以减小状态量和量测量之间的差值作为目标函数，是为了估计一种已经存在的系统状态。

本文针对配电网的特点，利用了最优潮流的思想，建立了配电网的状态估计。和传统的状态估计以多估少不同，利用潮流的内在联系，通过目标函数的实现和不等式约束箝制作用，实现配电网状态估计以少估多的目标，是最优潮流在状态估计中的一个新应用。

1.3 模型求解方法

配电网通常是辐射状运行，为其专门开发的前推回代迭代法具有计算速度快、收敛性好和内存占用少的优点［15］。但是前推回代迭代法也存在难以处理PV节点弱环网的不足，变压器π型等值和补偿电容等值的对地导纳也会导致潮流不收敛［15-16］。牛顿-拉夫逊法等利用了导数信息的方法，可以用于输电网，也可以用于配电网潮流计算中。这类算法虽然在计算过程中需要重新生成雅可比矩阵，且配电网节点多也导致导纳矩阵规模较大，但其收敛性与专门开发的配电网潮流算法相比并没有本质的劣势［17-19］。实际上由于利用了导数信息，这类算法应该有更好的收敛性。优化问题的求解比潮流计算有更大的难度，选择合适的求解算法变得至关重要。得益于现代计算机技术的进步，配电网计算已不需要考虑内存占用和计算时间的问题，为了保证收敛性应选择鲁棒性较好的算法。

由式（2）—（6）描述的问题的基本形式与最优潮流问题类似，可以用求解最优潮流的方法进行求解。内点法是一种求解非线性优化问题的方法，属于需要导数信息的一类算法，能够实现最优潮流在线计算，广泛用于求解电力系统最优化问题。本文采用文献［20］中的内点法求解基于状态估计的智能配电网理论线损计算模型。虽然文献［20］只是将内点法用于输电网，但其应用范围也可拓展到配电网；且由于利用了雅可比矩阵和海森矩阵，其应用到配电网计算中也具有稳定性好、计算速度快的优点。

2 智能配电网量测终端配置

为了适应智能电网的要求，很多配电网在多处都装有量测终端采集并上传运行数据。由于分布区域广，配变的运行数据常常通过GPRS网络传输到数据中心，由此带来的一个问题就是信号不稳定，有时甚至丢失信号。正常情况下量测终端每15 min采集一次数据并上传到供电局数据中心。

智能配电网量测终端的典型配置如图1所示。由图1可见，并不是所有变压器上都装有量测终端，现场量测终端覆盖率无法达到100%，监测配电网实时运行情况存在一定困难。馈线由变电站母线引出，头节点电压即为母线电压。头节点注入功率由变电站馈线出口处量测装置采集。可以假设变电站内采集的数据是没有被误差污染的实际值，直接作为常数加入方程中。相对于变压器量测终端上传的数据，变电站内采集的数据误差较小，因而这样的假设是可以接受的。

图1 配电网量测终端典型配置Fig.1 Typical configuration of distribution network measuring terminals

正常情况下，配电网量测终端会定时通过无线传输方式上传变压器运行数据到供电局的营配一体化系统。对于那些无法上传数据的配电网量测终端，供电局会安排专门人员到现场拷贝数据，然后导入系统中。当系统中的记录足够多便可以画出各个量测点典型负荷曲线。一般而言，用户按其用电特性可以分为工业负荷、商业负荷、居民负荷3类，其负荷曲线也有所不同。

图2中实线表示的是居民用户典型负荷曲线，虚线表示的是考虑波动后的负荷上下界，可以根据历史数据在典型负荷曲线基础上乘以一定系数，得到其每个时刻运行的可行域。若预测负荷在某些节日会有较大变化，可以适当增加2条虚线之间的距离。合理的上下界应考虑负荷可能出现的最大或最小值，过大或过小都会影响模型的估计精度。进行计算时可以用典型负荷曲线作为初值，以虚线值作为不等式约束中负荷的上、下界。

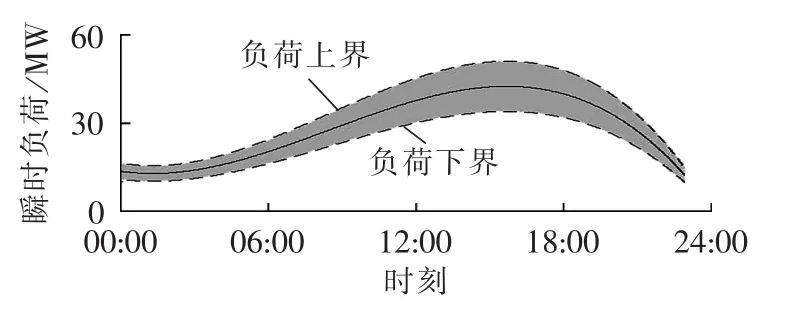
图2 某点居民用户典型负荷曲线Fig.2 Typical residential load curve

3 算例分析

3.1 算例介绍

现以1条实际辐射型配电线路为例进行说明，采用现场数据进行计算。线路基本信息如下：节点数为206，负荷数为62，计算时刻为高峰期20∶00，线路总长为11.91 km，线路主干线长度为3.59 km，变压器总容量为22290 kV·A。

为了简化讨论，认为典型负荷曲线的值与现场数据的值一致，现场数据作为真值使用。除非特别说明，分别在典型负荷曲线上乘以1.2和0.8作为负荷上、下界，即认为实际负荷在典型负荷曲线的±20%范围内。线损情况只计算到10 kV线路及变压器。选择基准电压为10 kV，节点电压标幺值为1，电压上、下界标幺值分别为1.07和0.93。实际线损计算中用到的数据都不是真实值，而是被噪声污染后的量测值，为了模拟实际情况可以在真实值的基础上叠加一定的噪声。负荷节点处功率量测值由以下公式计算：

其中，Xi为量测值；φ为服从正态分布标准差σ=0.05的随机数；X0为真实值。

3.2 情形讨论

为了分析所提模型和方法的适用性，分别考虑了智能配电网可能存在的4种情形。

a.负荷功率100%可知。

假设可以获得所有节点的功率，这种情形模拟了配电网量测终端覆盖率100%且都正常运行的情况，也是最理想的情况。此时目标函数式（2）中包含所有负荷的量测值，所有负荷的量测值都按式（10）叠加噪声。

b.负荷功率50%可知。

假设有10个节点的负荷功率未知，即只能采集到50%的数据，这是与现场实际比较相符的一种情况。一般而言，配电线路上既有供电局负责维护的公共变压器，也会有用户自己购买和管理的专用变压器。出于经济上的考虑，用户往往不会在专用变压器上安装与公共变压器一样的量测终端，这部分变压器也不能实时上传负荷；受设备制造水平限制，公共变压器上的量测终端也无法保证所有时间都正常工作，总有出现故障不能上传数据的时候。这2个因素使得真正可用的数据比较少。这种情形下目标函数式（2）中只包含可知负荷的量测值，量测值由式（10）叠加噪声得到。

c.始端功率可知。

假设只知道头节点功率数据，这是最极端的一种情形。一些新建设的线路可能已经装有量测终端，但在线路刚开始投入运行时还没有启用，此时只能通过变电站内部量测设备监测线路的送电情况。在一些配电网自动化程度比较低的地方，配电线路也只有来自变电站内部的送电数据。此种情形下目标函数式（2）中不包含任何一个量测量。

d.典型负荷曲线偏差大。

这种情形在始端可知情形下增加了对典型负荷曲线与实际负荷值差别较大情况的考虑，这时依据典型负荷曲线设置的上界或下界较接近实际值。算例仿真时在62个负荷中随机选取5个，认为其典型负荷曲线低于实际负荷25%，为实际负荷的75%，且实际负荷有60%的波动范围，分别在其典型负荷曲线上乘以1.05和0.45作为负荷上、下界。又另随机选取5个负荷，认为其典型负荷曲线高于实际负荷25%，分别在其典型负荷曲线上乘以1.55和0.95作为负荷上、下界。

4种情形下的等式与不等式约束都要计算所有节点，头节点功率不叠加噪声作为常数直接加入潮流方程中。

3.3 评价标准

借用状态估计相关标准进行评价，仿真测试时统计了最大偏差率和估计误差统计值作为估计性能指标，其中估计误差统计值和最大偏差率的计算公式分别为式（11）、（12）［8］：

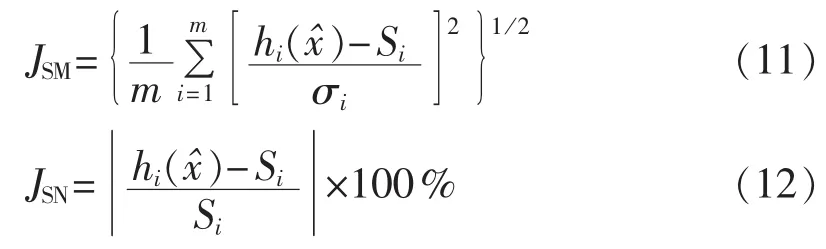
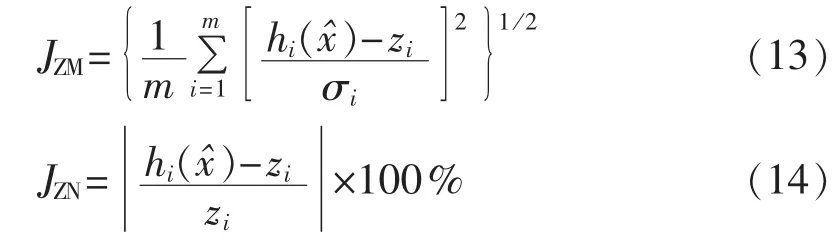
3.4 分析和讨论

4种情形的估计性能指标示于表1、2中。负荷功率100%可知、负荷功率50%可知以及始端功率可知这3种情形依次代表了量测量个数由多到少的3种情况。由JSM和JSN的变化可见，随着量测量个数的减少，估计结果与真实值的差距也相应减小。其变化可以这样解释，由于量测值是在真实值基础上叠加噪声得到，2个值之间必然存在差别，目标函数式（2）的作用是使估计结果尽量与量测值一致，显然与量测值的偏差越大，与真实值的偏差就越小。

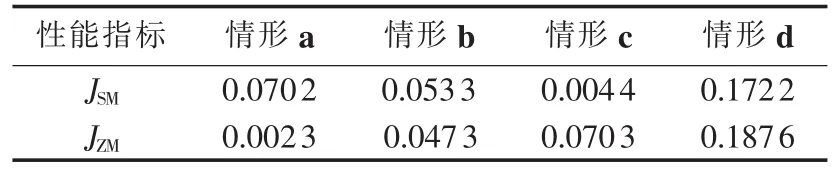
表1 20∶00时刻状态估计统计误差Table 1 Statistical error of state estimation at 20∶00

表2 20∶00时刻状态估计相对误差Table 2 Relative error of state estimation at 20∶00

现场数据的真实值是不可知的，只能相信量测值比较接近真实值，通过估计结果接近量测值来逼近真实值，且量测量越多接近效果越好。由JZM和JZN的变化趋势可看出当可获取的数据量较多时，估计结果与量测值的偏差比较小，在负荷功率100%可知的情形中，JZM几乎为0。仿真结果与对模型的期盼一致。

始端可知的情形中，目标函数对状态量的估计没有作用，仍然依靠头节点功率以及潮流方程式（3）得到了估计值，由表1、2中数值表明在该情形下与量测值和真实值的最大偏差都小于15%，说明本文提出的模型能很好地克服配电网因数据量少而不能进行理论线损计算的问题，在几乎没有量测量的情形下估计结果都有较高精度。

典型负荷曲线偏差大的情形下既没有负荷功率量测值，典型负荷曲线也没有很好地给出负荷的上下界，可用数据是所有情形中最差的，导致估计精度相对较低。

值得注意的是，4种情形下JSM都小于1，全部符合状态估计的要求。随着量测终端的升级换代，量测值的精度会逐渐提高，易知在量测值与真实值相差很小的情况下估计结果便会和真实值基本一致。

估计性能指标表达的意义较抽象，一般而言电力公司更愿意用合格率来评估状态估计的质量，其计算公式如下：

利用文献［21］中的公式：

本文中 αi取值 3σi，σi=0.05。和 zi分别对应正态分布的期望μ和随机变量。由概率论的知识可知，正态分布概率密度曲线99.73%的面积在μ±3σ的范围内，若 zi与之间的距离大于 3σ，便认为小概率事件发生了，所以这个点的估计是不合格的。若式（16）成立，则认为点估计合格。实际生产中，状态估计合格率要求达到98%以上［22］。

对3种情形下的合格率进行仿真测试，结果如表3所示。

由于始端可知和典型负荷曲线偏差大的情形中没有量测值，所以不计算合格点数。由前面估计性能指标的测试可知，负荷功率100%可知和负荷功率50%可知的情形下估计结果都很理想，表3中所有点估计合格也在意料之中，满足实际工程应用要求。

表3 20∶00时刻状态估计合格率Table 3 Qualified rate of state estimation at 20∶00

获得各种状态量的估计结果后可以很容易地计算配电网线损情况。总的网损用下式计算：

其中，Pr为头节点有功功率；PD，i为状态值，是 PD中的第i个元素。式（17）得到的只是功率值，实际线损计算中常用电量值。可以将线损计算时间等分为N个时间段，利用

作为功率在时间段上的积分，从而得到近似的电量。其中，Δti表示时间段长度，本文选取Δti为15 min；表示在这个时间段内任意一点的瞬时功率。

为了进行比较分析，4种情形下计算的网损与等值电阻法计算的损耗一同列在表4中进行比较，所计算的总损耗为24 h总的有功损耗。等值电阻法采用文献［23］中介绍的公式。

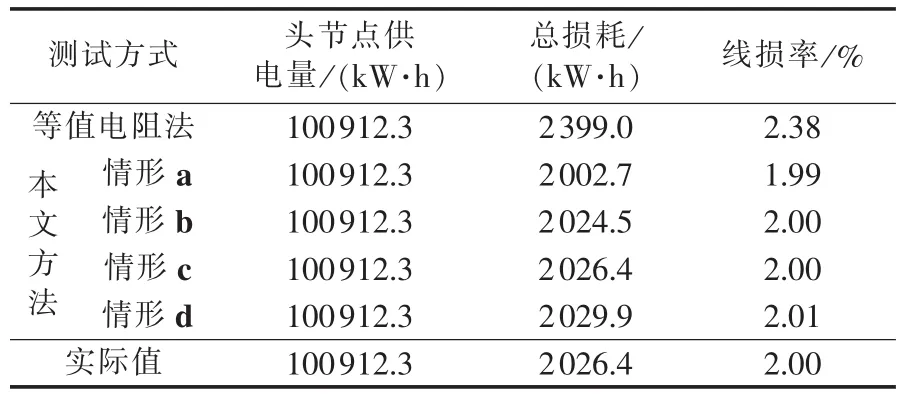
表4 24 h网损计算结果Table 4 Results of power loss calculation for 24 hours

本文涉及的是理论线损计算的内容，并不对管理线损进行讨论，下文提到的真实值都是理论计算的值，而不是现场实际值。

由表4中的结果可以看到等值电阻法计算的网损与实际值相差较大。由于等值电阻法的基本思想是依据变压器容量对负荷平均分配，没有考虑变压器负载率，计算所用的均方根电流不能代表一整天的电流情况，计算的理论线损与实际值差别较大。本文所介绍的方法在4种情形下网损的计算结果基本相同，即使在典型负荷曲线偏差大时也能得到与实际值基本一致的线损计算结果，这是因为虽然某些数值较小的估计值相对误差大，但绝对误差并不大，所以最终线损计算结果与真实值相差不大。

进行线损计算时不仅需知总的有功损耗，还需知每条分支线路上的有功损耗情况，从而找出损耗较严重的线路进行降损。直接用估计结果计算4种情形下20∶00—21∶00的线损。分支线路有功损耗的情况列在表5中，由于数据比较多，只以降序列出损耗最大的几条线路的有功损耗。类似地，表6中也以降序列出损耗最大的几个变压器支路的有功损耗。

表5 20∶00至 21∶00分支线路有功损耗Table 5 Active power loss from 20∶00 to 21∶00 for branches

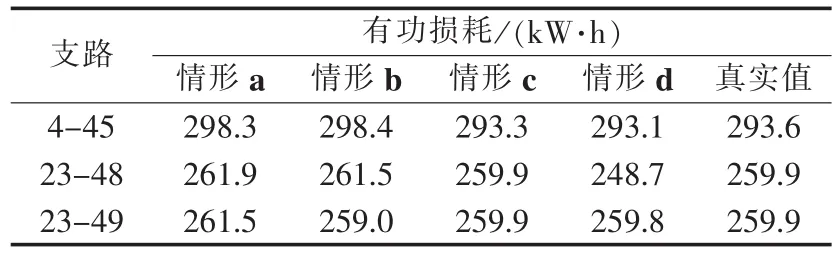
表6 20∶00至21∶00变压器支路有功损耗Table 6 Active power loss from 20∶00 to 21∶00 for transformer branches

表5、6显示利用测量值计算的损耗误差较大，4种情形下支路损耗与真实值基本一致，说明本文提出的方法能有效克服量测值存在误差导致计算结果偏差大的问题。其中，节点14、23之间线路的线损较大，应仔细分析损耗较大的原因并提出整改措施。

4种情形下的电压分布如图3所示，其中，横坐标表示电压范围（标幺值），纵坐标表示落入此范围的节点电压数；测量值即指用负荷测量值进行潮流计算后得到的电压。显然4种情形下电压分布与真实值基本一致，而且都在正常范围内。

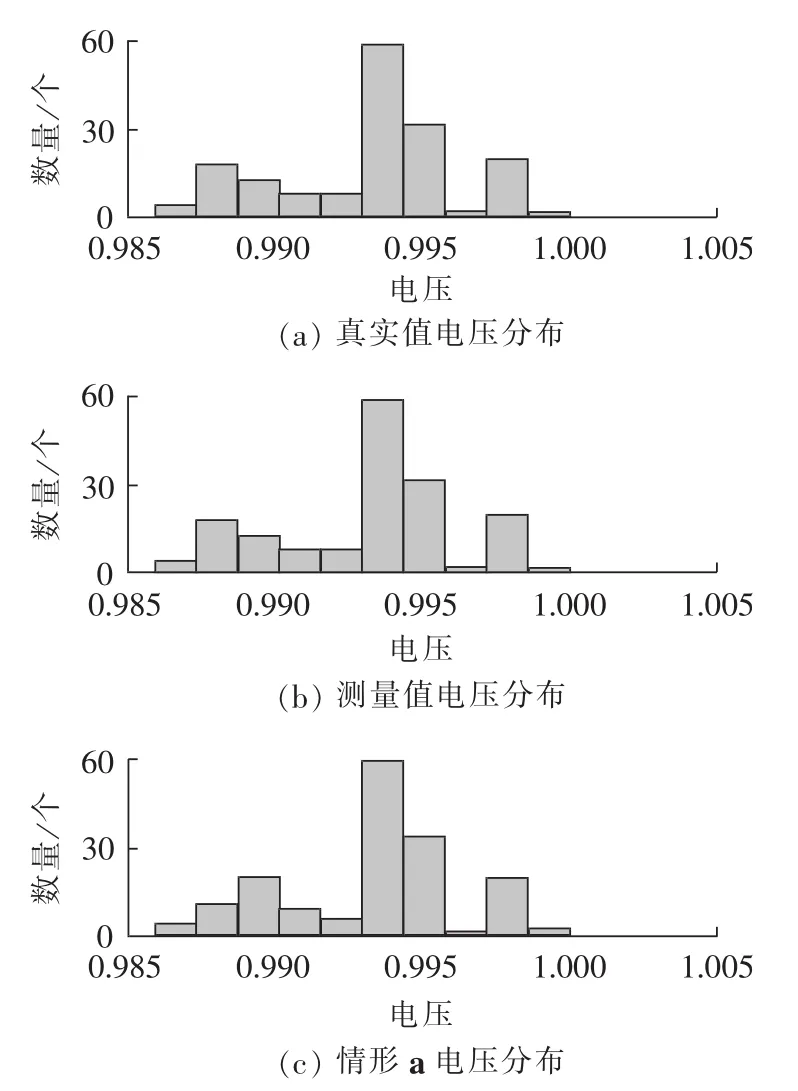
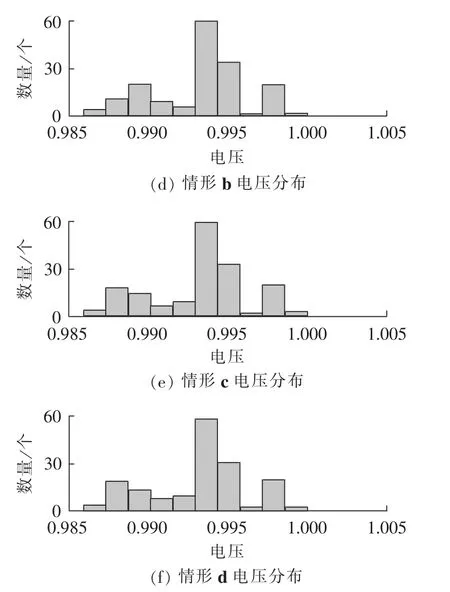
图3 20∶00时刻电压分布Fig.3 Voltage distribution at 20∶00

除计算各支路有功损耗外，所得负荷值也可作为已知量计算最优潮流，用优化理论制定降损措施。

4 结论

基于智能电网背景下量测终端的配置形式和特点，本文提出了一种新的配电网理论线损计算模型。模型基于状态估计原理还原被噪声污染的量测量或缺失信息，补充完善配电网状态量，进行配电网理论线损计算。仿真结果表明模型对量测量个数要求较低，只需要头节点功率数据就可以进行计算，量测量个数不同情形下计算结果基本相同。估计精度符合状态估计的要求，估计值合格率高，满足实际工程需求。与传统理论线损计算方法相比，本文模型计算的线损值更接近真实值，计算结果可作为最优潮流计算的输入数据。由于可以直接从配电网营配一体化系统中获取计算所需数据，本文方法及模型适合在线进行配电网理论线损计算，模型已用于国内某市配电网降损措施的制定，并取得了良好效果。