基于瞬时功率理论的输电线路分相电流差动保护

2014-09-27邓翔天袁荣湘肖振锋李体明李开文王娅镭

电力自动化设备 2014年11期

邓翔天，袁荣湘，肖振锋，李体明，李开文，王娅镭

（1.武汉大学电气工程学院，湖北武汉 430072；2.武汉大学动力与机械学院，湖北武汉 430072）

0 引言

电流差动保护原理简单，能够适应各种复杂的系统运行状态，具备天然的选相能力，因而常被用作超（特）高压输电线路［1-2］和大规模风电场并网［3-4］的主保护。但在实际应用中，电流差动保护易受分布电容电流的影响，尤其是随着特高压远距离输电技术的应用，分布电容电流已成为制约电流差动保护性能的重要因素［5-7］。

从补偿电容电流的角度出发，文献［8-9］提出一种计算电容电流相量的补偿方法。相量补偿法能对稳态电容电流进行补偿，但对故障初始阶段的暂态电容电流无法进行有效的补偿。文献［10-12］提出了基于贝瑞隆线路模型的电容电流精确补偿算法，即贝瑞隆线模法，其在理论上能够完全补偿分布电容电流，但其对采样频率、线路长度、线路参数的准确性等均有严格的要求，在工程实践中还存在诸多制约因素。文献［13-15］提出时域电容电流补偿算法，该算法在一定程度上突破了贝瑞隆线模法实用化的瓶颈，但仍然需要知道线路的精确参数；然而线路参数受运行方式、外界条件影响较大，很难得到精确值。从差动保护新原理出发，文献［16-17］提出一种基于模型识别的纵联差动保护判据，该方法从数学原理上解决了电容电流影响的问题，但原理、判据构造复杂，且仍需要线路参数，实际应用难度大。文献［18］提出一种利用差流中电阻性分量构造差动保护判据的方法，该方法的动作量中不包含电容电流，故避免了分布电容电流的影响；但该方法假设故障后电压相量等于故障前电压相量以提取电阻性电流，不适用于小过渡电阻的情况，因而不具备普遍的适用性。

为了解决传统功率定义体系不能满足现代电力装置发展需求的问题，研究人员提出并发展了瞬时功率理论体系，目前已将其成功应用于无功补偿、有源滤波和高压直流输电等诸多工程领域。在电力系统继电保护方面，瞬时功率理论也有许多应用。文献［19］利用瞬时功率理论计算故障时线路两侧系统的无功功率损耗，构建了新型的功率方向元件。该功率方向元件较传统方向元件在灵敏性、可靠性和快速性上均有较大改进。文献［20-21］提出了基于瞬时功率理论的电力变压器保护原理，其不受Y/△接线方式、铁损和涌流等因素影响。在线路保护方面，文献［22］利用瞬时功率理论提取线路电流的直流、反相和同极分量，并利用神经网络学习机进行相位估计进而实现故障判别。

值得注意的是，传统三相瞬时无功理论使用了三相变换，无法直接得到故障相。为解决上述问题，本文在瞬时功率理论的框架下，提出一种单相有功电流分量快速提取算法：通过三相数字锁相环获得线路两侧基波正序电压的相位信息［23-24］，将线路电流简单变换和滤波后得到与电压同相的基波有功电流分量（简称有功电流分量）的幅值；而分布电容电流和并联电抗器电感电流经过相同变换后与有功电流分量正交，故采用有功电流分量构造的差动保护判据从原理上不受电容电流的影响。本文使用PSCAD建立500kV输电线路模型，对该保护算法进行了仿真验证。

1 原理分析

1.1 输电线路模型

高压输电线路常用PI型等效模型。假设一条装有并联电抗器的500 kV输电线路MN，其系统图与等效电路图如图1所示。其中，UM、UN为线路两端电压相量；IM、IN为线路两端电流相量；ZL为线路阻抗；ZC为线路对地等效电容容抗；LM、LN为装设在线路两端的并联电抗器；ZLM、ZLN为并联电抗器的阻抗；ICM、ICN为线路两端等效电容电流相量；ILM、ILN为流经电抗器的电感电流。

图1 500 kV输电线路及其等效电路Fig.1 500 kV power transmission line and its equivalent circuit

正常运行或区域外故障时，线路段MN的差流Icd为：

由基本电路原理可知：电容电流ICM、ICN的相位分别超前电压 UM、UN的相位 90°；电感电流 ILM、ILN的相位分别滞后电压UM、UN的相位90°。

文献［18］提出的利用电阻性差流构造的差动保护判据在高阻故障时能够很好地提高差动保护的灵敏度，但当过渡电阻较小时，假设条件不再成立从而导致判据失效。本文利用单相瞬时功率理论提出了不受过渡电阻影响的“电阻性”电流分量，即有功电流分量的提取方法。

1.2 有功电流提取

文献［25-27］给出了单相电路瞬时谐波以及无功电流的实时检测方法，由于本文只需实时检测有功电流分量，因此可对该方法做适当简化。

假设线路电流瞬时值为 is（t），则有：

其中，ip（t）为基波有功分量；iq（t）为基波无功分量；ih（t）为所有高次谐波分量。

假设电网某相电压为：

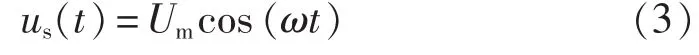
其中，Um为相电压幅值；ω为电压角速度。

用傅里叶级数表示式（2）可得：

其中，Ip为有功电流的幅值；Iq为无功电流的幅值；In和φn分别为n次谐波电流的幅值与初相角。

式（4）两边同乘以 2cos（ωt），可得：

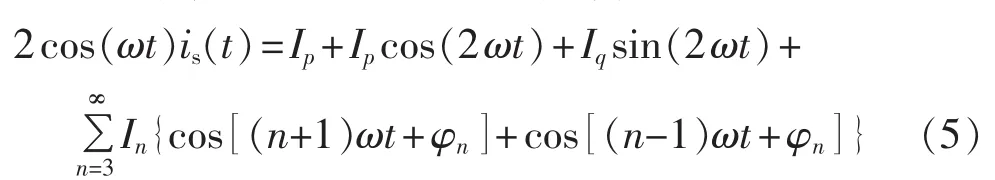
式（4）两边同乘以 2sin（ωt），可得：

由式（5）、（6）可知，经过变换后的电流均含有直流分量和交流分量。由瞬时功率理论的概念可知，直流分量对应变换前的基波分量，交流分量对应变换前的谐波分量。理论上，使用截止频率小于2倍基波频率的低通滤波器（LPF）对使用式（5）变换后的信号进行滤波，即可得到对应的有功电流分量的幅值。

根据系统的序网络可知，正序电压只由系统两侧的电源提供，故相对于单相电压锁相环，采用三相电压锁相环能够更好地抑制短路发生位置以及电压谐波等因素的影响［23-24］。单相有功电流瞬时检测算法框图如图2所示。其中，uabc为三相电压瞬时值；ia、ib、ic为三相电流瞬时值；iap、ibp、icp为三相电流的有功电流分量。

图2 三相有功电流提取Fig.2 Extraction of three-phase active-power current components

2 有功电流差动保护

2.1 内部故障分析

当线路内部发生接地故障时，假设M侧故障电流ifM为：

其中，ipM1为M侧故障电流的基波有功分量；iqM1为M侧基波无功电流分量；ihM为M侧高次谐波分量。

将式（5）和图2所示的基波有功电流分量提取方法应用于式（7）可得该采样时刻基波有功电流分量ipM的值为：

其中，IpM1为M侧基波有功电流的幅值。

同理可得，N侧故障电流的有功分量ipN为：

其中，IpN1为N侧基波有功电流的幅值。

假设M、N侧锁相环输出的相角分别为θM（t）和θN（t），则两侧电压相量的相位差 θMN为：

M、N侧的基波有功电流相量IpM1、IpN1的相位关系如图3所示。

图3 区内故障时线路两端有功电流分量的相位关系Fig.3 Phase relation of active-power current components between two line terminals for in-zone faults

由图3可知，基波有功电流差流相量Ipd为：

根据余弦定理，M、N侧基波有功电流差流的模值为：

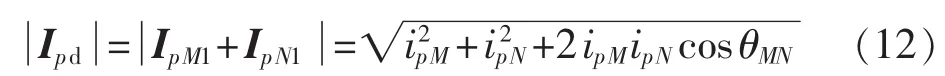
2.2 正常运行以及外部故障分析

正常运行或外部故障时，线路基波有功电流分量相量如图4所示。

图4 正常运行或区外故障时线路两端有功电流分量的相位关系Fig.4 Phase relation of active-power current components between two line terminals for normal operation and out-zone faults

M、N侧基波有功电流差流模值为：

当θMN≈0°时，由于区域内无电阻性对地支路，故两端有功电流大小相等、方向相反，基波有功电流差流为0。

2.3 保护判据

由于当最大正常运行方式或外部故障时线路两侧基波正序电压相位差并不一定近似为0°，故此时的有功电流差流也不一定近似为0°。为了增强有功电流差动保护判据应对正常运行和外部故障时的选择性，本文提出了带制动系数的有功电流差动保护，其判据如下：

2.4 比例制动系数Kap的整定原则

有功电流差动保护的比例系数Kap的整定原则为：躲过最大负荷电流和最大外部故障电流时的有功电流差流，确保有功电流差动保护判据在最大运行方式和外部故障时不动作。

3 仿真验证

3.1 模型搭建

参考文献［28］，使用PSCAD建立仿真模型，如图5所示。系统参数：M侧参数，EM=1.05∠0°p.u.，正序等效电阻RM1=1.051 5 Ω，正序等效电感LM1=0.13743 H，零序等效电阻RM0=0.6 Ω，零序等效电感LM0=0.0926 H；N 侧参数，EN=1∠-30°p.u.，正序等效电阻 RN1=26 Ω，正序等效电感LN1=0.14298 H，零序等效电阻RN0=20 Ω，零序等效电感LN0=0.11927 H；线路正序参数，r1=0.02083 Ω /km，l1=0.8948mH /km，c1=0.0129μF/km；线路零序参数，r0=0.1148Ω/km，l0=2.288 6 mH /km，c0=0.005 23 μF/km；线路长度为300 km，QFM为 M侧断路器，QFN为 N侧断路器，QFLM为M侧并联电抗断路器，QFLN为N侧并联电抗断路器，并联电抗器电抗补偿度为60°；故障点在F处，三相电压、电流采样频率为5 kHz；XL为三相并联电抗器的感抗；XN为中性点电抗器的感抗。

图5 500 kV输电线路仿真模型Fig.5 Simulation model of 500 kV power transmission line

3.2 空载合闸情况下的仿真验证

假设N侧断路器QFN断开，并联电抗器退出运行，M侧断路器在1.2s时合闸。由于线路空载合闸时的电流主要为电容电流，因此空载合闸情况最能考察不同方案抑制电容电流的能力。有功电流法、时域补偿法及传统方法的差流如图6所示。由图可知，未采用补偿措施的传统方法差流最大值为0.48 kA，采用时域补偿法和有功电流法的差流的最大值分别为0.096 kA和0.048 kA；传统方法差流的稳态值为0.4 kA，时域补偿法的稳态值为0.028 kA，有功电流法的稳态值几乎为0。分析可知，有功电流法对暂态电容电流的抑制效果优于时域补偿法，并且能够完全抑制稳态电容电流。

图6 空载合闸时，3种保护判据得到的差动电流Fig.6 Differential current of no-load closure for three criteria

3.3 外部故障仿真验证及比例系数Kap的整定

假设系统的最大运行方式为：EM=1.05∠0°p.u.，EN=1∠-60°p.u.，在 1s时 M、N 侧外部出口分别发生三相金属性短路接地故障。以A相为例，动作量与制动量的比值K′ap如图7所示，K′ap的计算公式如下：

图7 区外故障时，本文判据得到的A相有功差动电流及其与制动电流的比值Fig.7 Phase-A differential active-power current obtained by proposed criterion and its ratio to breaking current for out-zone faults

由图7可知，最大运行方式下发生外部故障时，其有功差流最大可达到0.6 kA，对应的动作量与制动量的比值 K′ap为0.19。以1.2倍裕量整定比例制动系数 Kap，可得 Kap=0.228。

3.4 内部故障仿真验证

3.4.1 不同故障类型时的有功差流

当故障点F位于线路MN中点时，假设在1s时分别发生金属性A相单相接地故障、AB相间短路故障、AB相间短路接地故障和三相短路接地故障，A、B、C相的有功电流差流如图8所示。

图8 发生不同类型的区内故障时，本文判据得到的三相有功差动电流Fig.8 Three-phase differential active-power currents obtained by proposed criterion for different in-zone faults

A、B、C相对应的K′ap如图9所示。由图7和图9可知，有功电流分相差动保护能够很好地识别内部外部金属性短路故障，并具备选相能力。

3.4.2 并联电抗器对有功电流差流的影响

五是做好流域水功能区纳污红线考核支撑。从2014年开始，国家对重要水功能区进行考核。长江流域水资源保护局负责组织流域水功能区考核的技术工作，组织制定流域水功能区水质达标评价技术细则，每年与地方协调制定年度水功能区考核名录和监测方案，并对各省区监测的水功能区评价结果进行复核，形成复核报告上报水利部。在最严格水资源管理制度考核中，长江流域水资源保护局也按照国务院考核组的统一部署，参与部分省区的考核，并提供长江流域的水功能区考核基础信息，有力的支撑了流域水功能区纳污红线考核工作[7]。

控制断路器QFLM和QFLN的分合，以控制并联电抗器投运状态。当线路中点位置在1s时发生经不同过渡电阻接地的单相短路故障时，故障相有功电流差流波形如图10所示。由图可知：系统正常运行时，并联电抗器对有功电流差流不造成影响；发生金属性短路接地故障后，投入并联电抗器比未投入情况下的有功电流差流低7%；当过渡电阻为500Ω时，投入并联电抗器比未投入情况下的有功电流差流低5%。综合分析，并联电抗器的投运情况对有功电流差流的影响较小，可忽略不计。

3.4.3 过渡电阻的影响

由式（14）可知，有功电流差动保护判据的浮动门槛值Ipres为：

传统带制动系数的电流差动保护判据为：

同理，传统带制动系数的电流差动保护判据的浮动门槛值Itres为：

图9 发生不同类型的区内故障时，本文判据得到的有功差动电流与制动电流的比值Fig.9 Ratio of differential active-power current obtained by proposed criterion to breaking current for different in-zone faults

图10 投入并联电抗器前后，本文判据得到的有功差动电流Fig.10 Differential active-power current obtained by proposed criterion，with and without shunt reactor

以单相短路接地故障为例，通过设置不同的单相短路接地过渡电阻值分析传统电流差动保护判据和有功电流差动保护判据对过渡电阻的耐受能力。假设单相接地故障位于线路MN内距母线N的1 km处，过渡电阻取值范围为50～900Ω，以50 Ω为步进。在相同条件下，传统带制动系数的电流差动保护的比例系数Kt整定为0.7。传统电流差动保护的差流与有功电流差流及各自对应的浮动门槛值见图11。

图11 过渡电阻不同的单相接地故障下，传统电流差动保护判据和本文判据得到的差动电流及其浮动门槛值Fig.11 Differential active-power current obtained by traditional and proposed criteria and corresponding floating thresholds for different transition resistances of single-phase grounding fault

由图11可知：发生内部故障时，在相同过渡电阻条件下，有功电流差流略低于传统差流；随着过渡电阻的不断增大，有功电流差动保护浮动门槛值的增加幅度明显小于传统电流差动保护浮动门槛值的增加幅度。其原因为：内部故障时，传统差流由电阻性和电容性分量构成，且电阻性分量为主要成分，而有功电流差流只包含电阻性分量，故在相同过渡电阻条件下，二者差异较小。在外部故障或空载合闸时，有功电流差流明显小于传统差流，故有功电流差动保护的整定值小于传统电流差动保护的整定值，确保了有功电流差动保护判据在高阻接地故障时仍然可正确区分内外部故障。

在相同条件下对采用了时域补偿法的电流差动保护判据进行整定，按照式（19）计算保护判据的灵敏度系数S。

不同方法的灵敏度曲线见图12。由图12可知，当过渡电阻大于300 Ω时，未采取补偿措施的判据已无法准确判断内部故障；当过渡电阻大于600 Ω时，时域补偿法也不能准确判断内部故障；当过渡电阻达到900 Ω时，本文提出的有功电流法仍然可以准确判断内部故障。分析发现：在抑制电容电流影响和耐过渡电阻能力方面，有功电流法明显优于时域补偿法和传统差动保护方法；此外，不同于时域补偿法，有功电流法无需使用线路阻抗的参数，提高了保护算法的适应性。