Turbo乘积码译码算法的简化

柳 昭，张晓明，韩月平，宋庆国

(山东航天电子技术研究所 山东 烟台 264003)

1993年Berrou等学者提出了基于软输入软输出(Soft Input Soft Output，SISO)迭代译码算法的Turbo码[1]。由于Turbo码具有接近香农限的优异性能，使之成为信道编码领域的研究热点。1994年，Pyndiah将Turbo码的子码码型拓展到线性分组码，认为由分组码串行级联构造的Turbo码同样具较好的性能。Pyndiah还设计出可以实现SISO的迭代Chase译码算法[2]，并将其应用于乘积码的译码，给出了一种译码方法类似Turbo码的SISO迭代译码算法，从而提出了Turbo乘积码(Turbo Product Code，TPC)的概念。

1998年Pyndiah针对TPC提出一种修正的Chase译码算法[3]，这是一种近似的最大似然译码，可以获得接近Shannon极限的纠错性能。但是这种算法需要大量的运算来寻找竞争码字和计算软输出，因此译码复杂度高，延时大。近几年来，有不少学者提出了TPC改进译码算法[4-5]，如梯度算法[6]、并行译码算法等。这些算法在一定程度上减少了运算量，降低了系统延时，但是由于在迭代译码中仍然需要寻找竞争码字和计算软输出，所以算法的复杂度并未实质降低。

本文在传统Chase算法的基础上，提出了两种新的简化方法，这两种方法不再需要寻找竞争码字和计算软输出，大大减小了算法的计算量，提高了算法的译码速度。

1 传统Chase算法

硬判决译码，即代数译码，先用一个固定的判决门限，把超过门限电压的信号判为逻辑 ，把低于门限电压的信号判为逻辑 ，然后利用校验子结合奇偶校验位进行纠错。软判决译码，是指先把解调器输出的抽样电压进行Q进制（Q=2m,m＞1）电平量化，再送给译码器进行译码。Chase软判决译码算法是一种软输入硬输出(Soft Input Hard Output，SIHO)译码算法，译出的码字为硬输出。

1.1 Chase算法

假设二进制信息码元{0，1}通过分量码都为线性分组码（n,k,d） 的二维TPC编码器，经BPSK调制后得到发送码字E=（e1,e2, …,en），，再经AWGN信道中传输，N=（n1,n2, …,nn）信道噪声 的均值为0，方差为σ2。接收码字为R=（r1,r2, …,rn），三者满足：R=E+N。Chase算法实现方法步骤[3]如下：

步骤1：对接收码字R进行硬判决得到Y=（y1,y2, …,yn），yj∈{,}0 1 。

步骤2：确定Y的p=[d/2]个最不可靠位，记录其位置。

确定最不可靠位是通过考察yj的可靠度得出的，码元yj的可靠度定义如下：

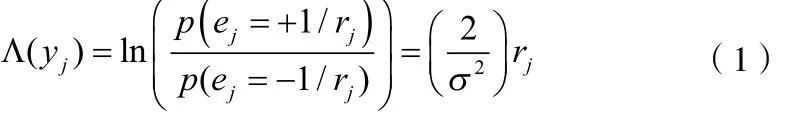
p（ej= +1/rj）为信道的转移概率，推导过程参考文献[3]。经归一化后，码元yj的可靠度可通过考察|rj |得到， |rj |值越小，可靠度越低。

步骤3：构造测试图样T q。分别在p个不可靠位置上取'0'和'1' ，'0' 其它位置取 ，构造一个由2p个n维向量组成的测试图样T q。

步骤5：将Z q进行代数译码（即硬判决译码）。得到译码结果C i，将译码结果作如下映射：0映射成-1，1映射成+1，后归入集合Ω 。

步骤6：计算集合Ω中的码字C i与接收信号R间的欧氏距离，选出欧氏距离最小的码字作为候选码字D。欧氏距离的计算如下：

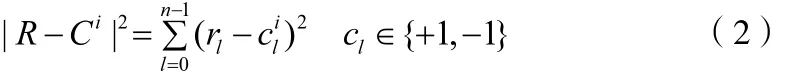
1.2 基于Chase算法的软入软出译码算法

上述Chase算法译出的码字为硬输出，纠错能力不能得到保证。为了提高TPC的译码性能，必须采用迭代译码方式，这就需要保证译码器的输出为软数据。下面直接给出译码器软输出值的计算公式，推导过程参考文献[3]。译码器的软输出值为：

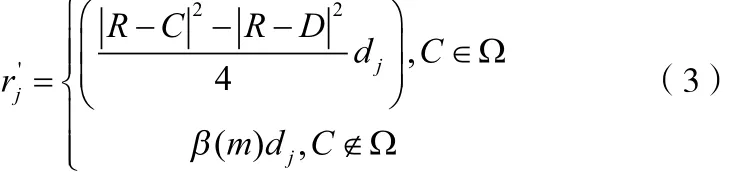
其中，R为接收序列，它是经过解调器解调和Q进制量化得到的软数据；D为经过SIHO译码得到的候选码字；C为D的竞争码字，C满足：与接收序列R的欧式距离最小，且Cj≠Dj。由于在候选码字集合Ω中存在找不到竞争码字C的可能，此时可用含可信度因子β(m)的式子来近似计算，β(m)≥0，在实际的工程实践中，β(m)值主要通过仿真实验来确定。用软输出值减去软输入值，就可以得到外部信息。

2 影响算法复杂度的关键因素分析

第1节中介绍的传统Chase算法在硬件上实现比较复杂，主要原因是欧氏距离的计算以及寻找竞争码字C需要大量的运算。欧氏距离的计算可以用相关值的计算进行简化，欧氏距离最小等价于相关值最大[7]。寻找竞争码字C就成为影响算法译码复杂度的关键因素。

竞争码字C同时满足两个条件：1）与接收序列R的欧式距离最小；2）Cj≠Dj。传统Chase迭代译码算法是将条件b放在前[3]，先判断Cj≠dj，在候选码字Ω集合中找到Cj≠dj的序列，把找到的序列放入子集Ω1中，Ω1Ω；然后在Ω1中找到与接收序列R有最大相关值的序列作为竞

争码字C。用传统方法寻找竞争码字C半次迭代需要进行n2×(2p-1)次比较，动态构建n2个子集Ω1 ，进行n2次排序计算。传统方法寻找竞争码字C的过程相当繁琐，逐行或逐列译码时每个码元的竞争码字C是动态变化的。

3 新的简化译码算法

梯度算法的思想[6]是：为了简化外部信息的计算，在迭代译码时，用前一次迭代得到的候选码字D(m-2)来代替竞争码字C，省去了寻找竞争码字C的过程来降低译码复杂度。即当dj(m)≠dj(m-2)时，

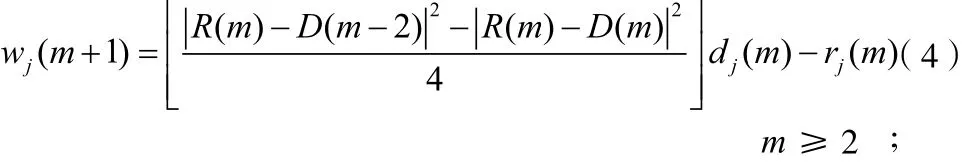
当dj(m) =dj(m-2)时，

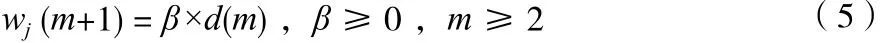
当m〈2时，仍应用Chase迭代译码算法进行译码，m≥2时用梯度算法进行译码， 为串行迭代译码的半迭代次数。由此可见，梯度算法尽管对传统的Chase算法有所简化，然而当m〈2时仍需繁琐的寻找竞争码字；当m≥2需要比对行和列的候选码字，而且部分码元的外部信息仍需通过公式（4）计算。因此，算法的复杂度仍然很大，并未实质减少。

在对梯度算法的研究中发现，行和列的候选码字大部分都保持不变，即dj(m)=dj(m-2)，此时外部信息大部分都为β(m)dj。因此在梯度算法的基础上提出两种简化方案。第一种简化方案是：不找竞争码字C，不再计算软输出，外部信息wj直接用经过SIHO译码得到的候选码字D乘以β(m)得到，即wj=β(m)dj，dj∈ { - 1 , 1 } 。此处可信度因子β(m)是经过Q进制量化得到的。

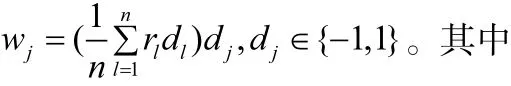
4 性能仿真

使用MATLAB编程工具进行定点数仿真实验，子码选取（64,57）×（64,57）的扩展汉明码构成二维TPC码，编码效率为0.793。调制方式为BPSK，传输信道为AWGN信道。不可靠码元个数p=3，采用串行迭代，迭代次数为3次，8bit量化，缩放因子α(m)=[0.0,0.2,0.3,0.5,0.7,0.9]，可信度因子β(m)=[0.2,0.4,0.6,0.8,1.0,1.0],设定参与仿真的码块个数为10 000，误码率仿真图如图1和图2所示。

由图1可以看出，在BER为10-6时，传统Chase算法译码可以获得大约6.6 dB的信道编码增益，相比硬判决译码，编码增益明显提高了大约2.5 dB。不找竞争码字，外部信息用 简化后，编码增益比传统Chase算法仅仅下降了0.5 dB，然而复杂度却大大降低。同时，简化算法比硬判决译码编码增益提高了2 dB。

由图2可以看出，在BER为10-6时，用β(m)简化算法后相比已有的梯度算法[6]编码增益下降了大约0.1 dB。若采用最大相关值的均值简化算法后，此时编码增益比梯度算法提高了大约0.1 dB，比传统Chase算法仅仅下降了0.3 dB，然而两种方法的译码过程比梯度算法和传统Chase算法都简单，复杂度大大降低。由上述分析可见，两种简化算法复杂度更低，实时性更好，而译码性能只是略微降低。

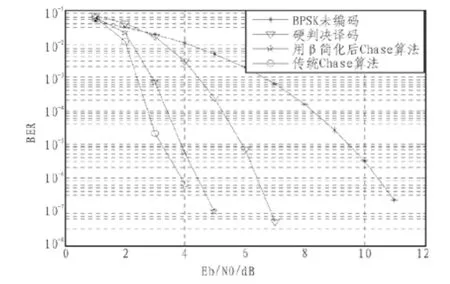
图1 简化后Chase算法译码性能Fig.1 Decoding performance of the simplified Chase algorithm

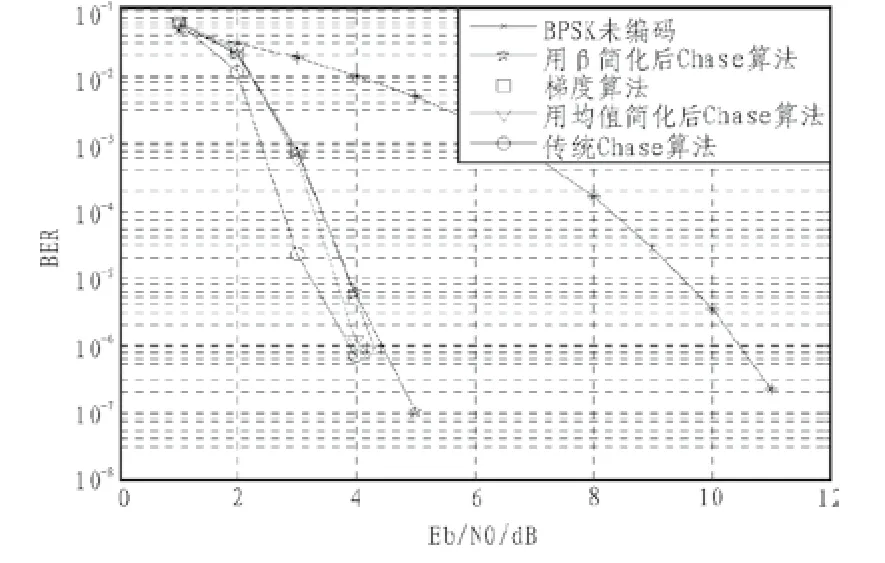
图2 简化后译码算法与梯度算法的对比Fig.2 Comparison of the simplified algorithm and gradient algorithm

5 结束语

文中在梯度算法的基础上介绍了两种新的TPC软判决串行简化迭代译码方法，以较小的性能代价换取了很大程度上译码复杂度的降低。用β(m)简化算法后可以获得大约6.1 dB的信道编码增益，相比传统Chase算法，编码增益下降了大约0.5 dB；而用最大相关值的平均值简化算法后可以获得大约6.3 dB的信道编码增益，相比传统Chase算法，编码增益仅仅下降了大约0.3 dB。两种简化算法能基本保持传统Chase算法的译码性能，然而译码复杂度却大大降低。这两种低复杂度算法非常适合硬件实现高码率实时译码，具有一定的工程实用参考价值。

[1]Berrou C,Glavieux A,Thitimajshima P. Near Shannon limit errorcorrecting coding and decoding :Turbo codes[C]// IEEE Int.Conf.Communications ICC’93.NewYork:IEEE,1993:1064-1071.

[2]Pyndiah P,Glavieux A,Picart A, et al. Near optimum decoding of product codes[C]//1994 IEEE GLOBECOM. New York: IEEE,1994:339-343.

[3]Pyndiah P. Near optimum decoding of product codes: block turbo codes[C]//IEEE Transaction on Communications. New York: IEEE,1998:1003-1010.

[4]黄小平，简福斌，谭燕庆. 一种新的Turbo乘积码简化迭代译码算法[J].计算机应用研究,2011,28(2):689-691 .

HUANG Xiao-ping，JIAN Fu-bin，TAN Yan-qing. New simplified iterative decoding algorithm for Turbo product codes[J]. Application Research of Computers,2011,28(2):689-691 .

[5]Chen Y，Parhik K. A very low complexity block Turbo decoder composed of extended hamming codes[C]//Proc of IEEE Global Telecommunications Conference.New York: IEEE, 2001:171-175.

[6]徐进延，李红信. Turbo乘积码梯度译码算法[J].通信技术，2008, 41(12) :81-83.

XU Jin-ting, LI Hong-xin.Study of Gradient Algorithm for Turbo Product Codes[J].Communications Technology, 2008, 41(12) :81-83.

[7]王玮，葛临东，巩克现. TPC基于相关运算的迭代译码算法[J]. 计算机应用，2010,30(7) :1760-1762.

WANG Wei，GE Lin-dong，GONG Ke-xian. Iterative decoding algorithm of TPC based on correlation computation[J]. Journal of Computer Applications,2010,30(7) :1760-1762.