基于新阈值函数的小波阈值降噪方法
2014-09-26宋倩倩
宋倩倩,双 凯
(中国石油大学(北京),北京,102249)
在信号的降噪问题中,小波降噪得到广泛应用,其中的模极大值和阈值降噪是最常用的两种方法。由于小波阈值降噪方法其实现简单、计算量小,从而在实际中得到广泛研究。小波阈值降噪算法中,小波最优分解层数的确定,以及小波阈值函数的选择,成为小波阈值降噪方法的关键[1-3]。
在小波阈值降噪中,文献[4]提出的传统硬阈值法可以很好地保留信号边缘等局部特征,然而在一些不连续点处有时会存在伪吉布斯现象。文献[5]提出的软阈值法克服了硬阈值存在的连续性差的问题,然而存在过于光滑而失去信号真实性的缺点。文献[6]提出的半软阈值法降噪效果虽略优于硬阈值和软阈值,但半软阈值函数形式与硬阈值、软阈值相同,信噪比改变不大。文献[7]提出的新阈值函数调节因子过多,而且没有给出如何针对不同的信号和噪声选取最合适的值。
本文针对小波阈值算法提出了一种新的阈值函数,在最优分解层数确定的基础上,采用传统阈值函数、改进阈值函数进行小波阈值降噪,通过matlab进行仿真,以信噪比SNR为性能指标,发现改进阈值函数优于传统阈值函数。同时发现,改进阈值函数选用阈值选取规则保守的minimaxi阈值,降噪效果优于其他阈值选取规则。
1 小波分析理论
根据小波Ψ(x)和尺度函数φ(x)为函数f(x)∈L2(R)定义小波序列展开[8],可知

其中,j0是任意开始尺度,Cj0(k)是近似值或尺度系数,dj(k)是细节或者小波系数。
小波分析,将信号分解到不同的分辨率上,像放大镜一样对信号在不同频带上进行分析。小波分析,解决了傅里叶分析不能解决的许多难题,使得信号可以同时具有时间域和频率域的信息。在低尺度上,具有较高的频率分辨率和较低的时间分辨率,在高尺度上具有较高的时间分辨率和较低的频率分辨率。
2 小波阈值降噪
小波变换具有一种“集中”的能力。经过小波变换后,有用信号对应的小波系数有很好的能量集中性,其幅值偏大,并且数量较少;而噪声信号对应的小波系数,能量比较平均,个数较多,但幅值偏小。利用含噪信号的这个特点,就可以通过合适的阈值函数将噪声对应的小波系数置零,从而实现有用信号的提取[9]。
一维含噪信号的小波阈值降噪处理过程步骤如下:
1)小波分解。选择一个合适的小波基,并通过白噪声检验来确定分解层数N,然后对信号进行N层小波分解。
2)小波系数的阈值处理。对第一层到第N层的高频系数,选取合适的阈值,根据相应的阈值函数进行阈值量化处理。
3)小波重构。对阈值处理过的小波系数,进行一维信号的小波重构。
2.1 阈值的选取
阈值的选取有4种原则:Stein风险阈值(rigrsure准则)、通用阈值(sqtwolog准则)、极大极小阈值法(minimaxi准则)、启发式阈值法(heursure准则)[10]。
4种阈值方法中,rigrsure准则和minimaxi准则的阈值选取较为保守,sqtwolog和heursure准则的阈值选取则较为过度,有可能将有用信号的高频部分当做噪声信号去除掉。本文选取保守的minimaxi阈值。
2.2 小波阈值函数
2.2.1 传统硬阈值和软阈值方法
硬阈值方法,是把绝对值小于阈值t的小波系数直接置零,其余的小波系数全部保留,实现信号的重构。硬阈值法的图像如图1(a)所示,公式为:
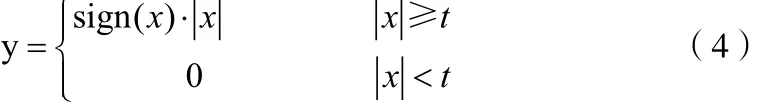
软阈值方法,是一种基于硬阈值法的改进,将硬阈值中保留的系数,绝对值减少t,再实现信号的重构。软阈值法的图像如图1(b)所示,公式为:
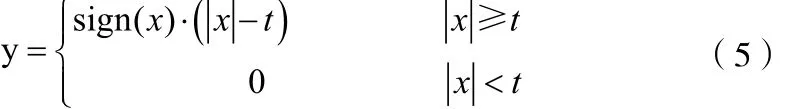
半软阈值方法,是对软、硬阈值法的一种折中方法,其函数值介于软阈值和硬阈值之间,在降噪中起到了很好的效果[11]。半软阈值的图像如图1(c)所示,公式为:
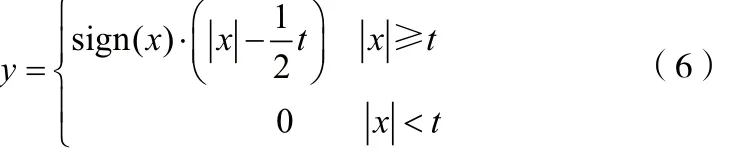
硬阈值函数在阈值处x=t是不连续不可导的,从而影响了信号重构的效果,带来了一些附加振荡,使信号光滑性很差。软阈值光滑性好,克服了硬阈值不够平滑的特点,但同时也由于过于平滑而损失了一些有用的高频信息,影响了重构的真实。半软阈值考虑到软硬阈值的缺点,是一种折中方法,取得了一定的降噪效果。本文针对传统阈值函数的缺点,提出两种改进阈值函数。

图1 传统阈值函数Fig.1 Traditional threshold function
2.2.2 改进阈值函数1
在硬阈值基础上进行改进,使其在保留了硬阈值函数优点的同时,又增加了连续性,以及光滑性。在阈值附近的区间(-(2-α)t, -t)∪(t, (2-α)t)上满足二次抛物线函数x= (1/m)y2+t,在剩余区间(-∞, -(2-α)t)∪((2-α)t, +∞)内满足硬阈值函数,在连接点x= (2-α)t处连续且可导。函数图像如图2所示,公式如下:

其中,m= 4(1-α)t,α∈ (0, 1)。
当α= 0时,接近于硬阈值,在区间(-2t, -t)∪(t, 2t)上满足抛物线函数,在(-∞, -2t)∪(2t, +∞)上满足硬阈值函数;当α= 1时,为软阈值函数;当α= 1/2时,接近于半软阈值,在区间(-3t/2, -t)∪(t, 3t/2)上满足抛物线函数,在(-∞,-3t/2)∪(3t/2, +∞)上满足硬阈值函数。α越接近于1,满足抛物线函数的区间越大,α越接近于0,满足抛物线函数的区间越小。
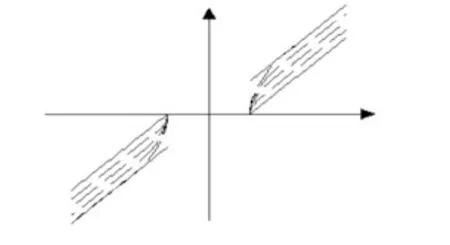
图2 改进阈值函数1Fig.2 Improved threshold function 1
2.2.3 改进阈值函数2
考虑到改进函数1到达硬阈值函数的区间太长,提出一个更快接近于硬阈值函数的函数。改进阈值函数1在区间(-(4-α)t/3, -t)∪(t, (4-α)t/3)上满足一个四次函数x= (1/m)y4+t,改进阈值函数1在区间(-∞, -(4-α)t/3)∪((4-α)t/3,+∞)上满足硬阈值函数,该函数在x= (4-α)t/3处连续且可导。此函数比改进硬阈值函数1能够以更快的速率连接到硬阈值函数。函数图像如图3所示,公式如下:

其中,m= 256[(1-α)t]3/27,α∈ (0, 1)。
当α= 0时,接近于硬阈值,在区间(-4t/3, -t)∪(t, 4t/3)上满足抛物线函数,在(-∞, -4t/3)∪(4t/3, +∞)上满足硬阈值函数;当α= 1时,为软阈值函数;当α= 1/2时,接近于半软阈值,在区间(-7t/6, -t)∪(t, 7t/6)上满足抛物线函数,在(-∞, -7t/6)∪(7t/6, +∞)上满足硬阈值函数。α越接近于1,满足抛物线函数的区间越大,α越接近于0,满足抛物线函数的区间越小。
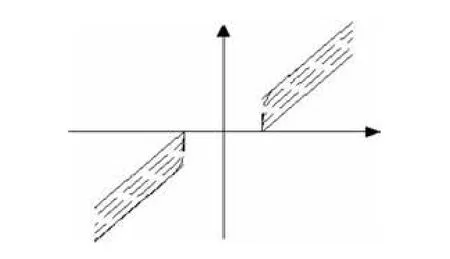
图3 改进阈值函数2Fig.3 Improved threshold function 2
阈值附近的系数混杂了干净信号的小波系数和噪声的小波系数,单纯阈值的选取无法改变这一问题。新改进的新阈值函数,将阈值 附近的系数做一定的能量压缩,从而在一定程度上压缩了噪声对干净信号的影响,同时又保留了部分干净信号的信息。两种改进的新阈值函数对阈值附近的系数做了不同程度能量的压缩,改进阈值函数1对小波系数的压缩区间长,而改进阈值函数2对小波系数的压缩区间短,要根据具体情况来选择这两种函数,以及合适的α值。
3 仿真验证
为了比较上述改进阈值降噪方法的降噪效果,引入如下信噪比定义:

其中:f(i)为真实信号,s(i)为含噪声信号,L为信号长度[12]。
采用db6小波函数,在叠加白噪声信噪比为3的情况下,对blocks信号,首先得出其最优分解层数为6层,然后采用改进阈值函数1和2进行降噪,并与传统硬阈值、软阈值、半软阈值进行比较,降噪后的信噪比如图4所示。

图4 blocks信号仿真Fig.4 Blocks signal de-noising of improved threshold function
图4可以看出,minimaxi阈值用在改进阈值函数中降噪效果最优,改进阈值函数总体降噪效果优于传统阈值函数。同时对于不同的α,降噪效果不同。在传统3种方法中,当硬阈值较优时,α贴近于1时效果更好;当软阈值较优时,α贴近于0效果更好。改进函数1和改进函数2总体走势相同,但不同的信号,不同的α值,去噪效果不同。
4 结 论
文中提出了一种压缩能量阈值函数,仿真发现,该函数采用minimaxi阈值可使改进阈值函数信噪比达到最优,两种改进阈值函数与传统阈值法相比,有着明显的降噪效果。在实际应用中,应该根据具体的信号具体的噪声采用不用的降噪策略,使得降噪效果达到最优。
[1]文莉,刘正士,葛云建.小波去噪的几种方法[J].合肥工业大学学报:自然科学版,2002,25(2):167-172.
WEN Li, LIU Zheng-shi, GE Yun-jian. Several methods of wavelet de-noising[J].Journal of He fei University of Technology:Natural Science,2002,25(2):167-172.
[2]乔强,周激流,何坤等,基于小波变换的非平稳信号去噪[J].
计算机应用研究, 2005 (8):161-166.
QIAO Qiang, ZHOU Ji-liu, HE Kun, et al. Noise reduction of non-stationary signal based on wavelet transform[J].Application Research of Computers, 2005(8):161-166.
[3]张翠芳.小波阈值降噪效果影响因素的研究[J].西安邮电学院学报,2008,13(5):13-15.
ZHANG Cui-fang. Research on the influence factors of wavelet threshold de-noising[J]. Journal of Xi'An University of Post and Telecommunications, 2008,13(5):13-15.
[4]Dohono D L, Johnstone I. Ideal spatial adaptation by wavelet shrinkage[J].biometrika, 1994,81(3):425-455.
[5]Dohono D L.Denoising by soft—thresholding[J].IEEE Transaction on Information,1995,41(3):613-627.
[6]栗鸣,郭东敏,权建峰,等.基于提升小波的改进半软阈值降噪方法[J],探测与控制学报,2009,31(4):54-57.
LI Ming, GUO Dong-min, QUAN Jian-feng,et al. Improved halfsoft threshold de-noising based on liftingwavelet[J]. Journal of Detection & Control, 2009,31(4):54-57.
[7]赵天娇,何选森,陈利.基于新阈值函数小波变化的噪声盲分离算法[J].计算机应用研究,2010,27(8): 2886-2888.
ZHAO Tian-qiao, HE Xuan-sen, CHEN Li. Noisy blind source separation algorithm based on new threshold function of wavelet transform[J]. Application Research of Computers. 2010,27(8):2886-2888.
[8]Rafael C. Gonzalez, Richard E. Woods. 数字图像处理[M].2版.阮秋琦,阮宇智,译.北京:电子工业出版社,2003.
[9]潘泉,张磊,孟晋丽等.小波滤波方法及应用[M].北京:清华大学出版社, 2005:58.
[10]胡泽,林丽君,何明格,等.基于小波变换的随钻测试数据降 噪方法研究[J].西南石油大学学报:自然科学版,2011, 33(1):165-169.
HU Ze, LIN Li-jun, He Ming-ge, et al. Research of de-noising oil-drilling testing data based on wavelet[J]. Journal of Southwest Petroleum University: Science & Technology Edition, 2011,33(1):165-169.
[11]刘俊星,章新华,周波等.新阈值及阈值函数的小波去噪研究,声学技术[M].上海:声学技术出版社, 2011.
[12]钱颖雪,左洪福,李耀华.小波与傅里叶变换耦合的静电监测信号去噪法[J].计算机技术与发展,2009,19(7):1-3.
QIAN Ying-xue, ZUO Hong-fu, LI Yao-hua. Static monitoring signal de-noising by wavelet and FFT[J]. Computer Technology and Development, 2009,19(7):1-3.
