3×4矩阵变换器的双电压控制策略

王汝田，崔永恒，陈酋峰，伏祥运

（1.东北电力大学 电气工程学院，吉林 吉林 132012；2.国网连云港供电公司，江苏 连云港 222004）

0 引言

矩阵变换器MC（Matrix Converter）与传统变换器相比具有许多优良的性能和优点，已经成为近年来研究的一个热点[1-12]。在这些研究文献中，大多数是针对三相输入三相输出的矩阵变换器（3×3 MC）拓扑结构带三相平衡负载进行研究。

随着电力电子技术的快速发展，各种非线性负载的应用越来越普遍，同时在实际中接于三相电源的负载也不一定是平衡负载，所以常要求变换器电源具有对不平衡和非线性负载供电的能力。对于3×3MC，当三相负载不平衡时，相电流的不平衡使得负载的中性点电位发生偏移，输出不对称的三相电压，从而影响负载的正常工作。三桥臂的变换器带不平衡负载时，负载电压不对称，有负序和零序电压，对于负序电压可以通过闭环控制来消除，但是对于零序电压却无能为力，这是三桥臂变换器自身拓扑所不能克服的[13-14]。

为了对不平衡负载供电，常用的方法是在3×3MC和负载之间加一个△/Y接线的变压器，但是其工作在基波频率，体积、重量较大，成本较高，使得MC体积小、功率密度高的优点荡然无存，这也使得MC的“全硅”概念失去了意义。文献[15-16]采用3×4 MC拓扑结构，将其中的一相桥臂（N相桥臂）直接连接到负载的中性点。文献[15]在双空间矢量调制的基础上，通过N相桥臂对负载的中性点电位进行控制，从而可以在不平衡负载的情况下输出三相对称的负载电压。文献[16]把双空间矢量调制方法中逆变级的调制改进为三维空间矢量调制，从而可以对零序电压进行控制，为不平衡负载提供三相对称的电压。

MC的双电压控制是一种典型的直接控制策略，与其他控制方法相比，具有如下突出优点：当三相输入电压不对称或含有谐波时，占空比的计算可以自动修正而不需额外的计算量，使输出电压仍然保持为所期望的参考正弦电压。这使得双电压控制策略在实际应用中具有一定的优越性。本文基于3×3 MC的双电压控制策略提出了3×4 MC的双电压控制策略。

1 3×4 MC的拓扑结构

3×4 MC和3×3 MC相比多出一相输出桥臂N，相应地多出了3个双向开关，其拓扑结构如图1所示。12个双向开关按照3×4的矩阵进行排列，通过双向开关的导通与关断，三相交流输入中的任意一相可以连接至四相交流输出中的任意一相。N相桥臂可以带负载ZN和A、B、C三相构成一个四相系统；也可以直接连接到三相负载的中性点（令ZN=0），用于控制中性点的电压，使得A、B、C三相输出电压波形为任意波形，或者是当三相负载为不平衡或非线性负载时，使得三相负载电压为三相对称电压。本文针对后者情况进行研究。为了分析3×4 MC中N相桥臂的控制方法，下面先对3×3 MC的双电压控制策略作简要介绍、推导。

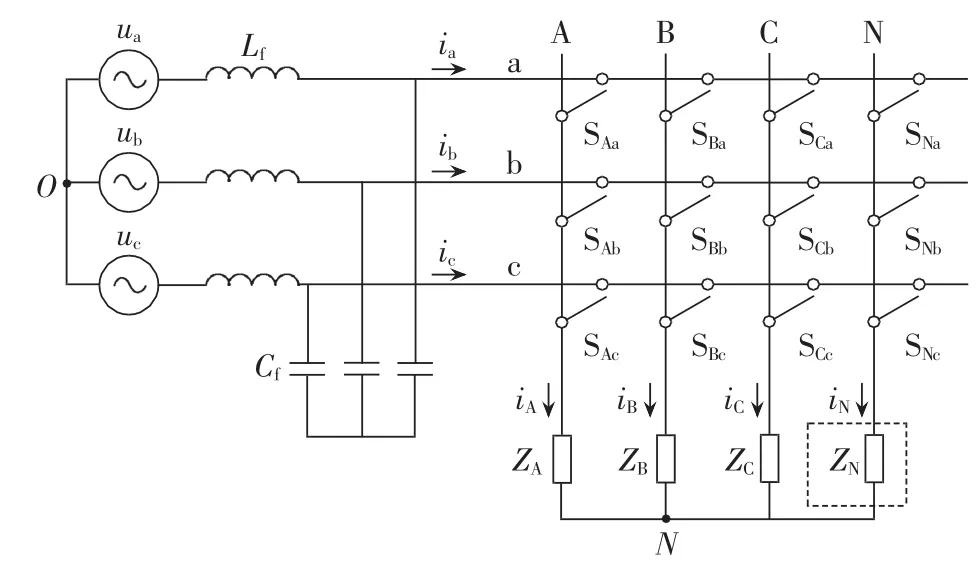
图1 3×4 MC的拓扑结构Fig.1 Topology of 3×4 MC

2 3×3 MC的双电压控制策略

图1中N相桥臂的3个开关始终断开，令其负载ZN=0，则变为 3×3 MC。

假设电网三相输入相电压的表达式为：

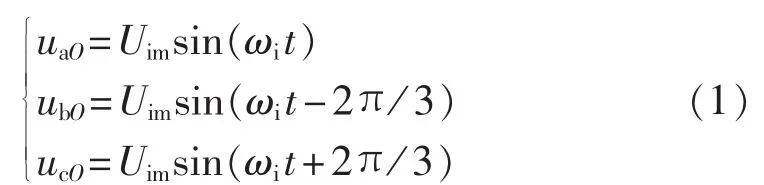
其中，Uim、ωi分别为输入相电压的幅值和角频率。

由图1可知，三相负载的中性点即为N点。假设参考三相输出相电压的表达式为：

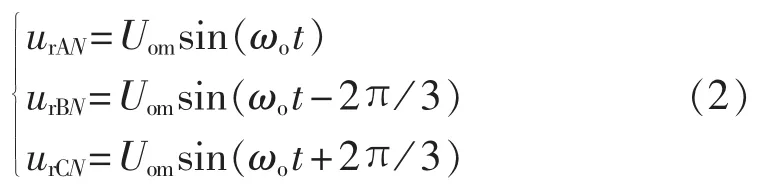
其中，Uom、ωo分别为参考输出相电压的幅值和角频率。

为了对MC进行调制，双电压控制策略将1个周期Ts内的输入、输出电压各分成6个区间，分别如图2和图3所示。

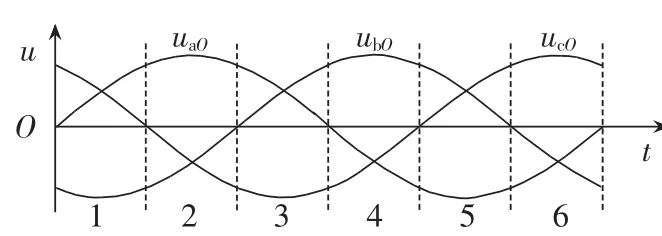
图2 输入电压区间划分Fig.2 Partition of input voltage

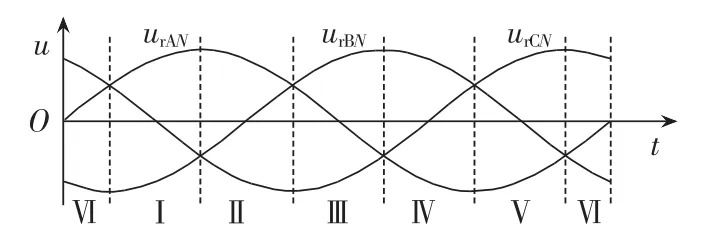
图3 输出电压区间划分Fig.3 Partition of output voltage

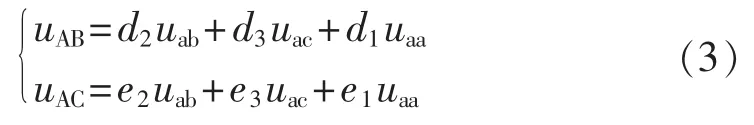
其中，d2、d3、d1和 e2、e3、e1分别为输入线电压 uab、uac、uaa在合成输出线电压uAB、uAC中被利用的占空比，并且有如式（4）所示的关系。

双电压控制策略[3]的原理是：在每个输入、输出电压扇区组合内，输出线电压由2个具有较大值的输入线电压和零电压采样合成，开关占空比与输入电压的瞬时值成正比，所得到的输出电压局部平均值为所期望的正弦参考电压。

例如输入电压在区间2、参考输出电压在区间I时，2个具有较大值的输入线电压为uab和uac。参考输出线电压urAB、urAC、urCB均为正值，这里选择被合成的输出线电压为urAB和urAC，因为这样选择可以使得MC工作过程中具有原点开关[7]，降低开关损耗。根据双电压合成方法的原理，可以得到输出的线电压为：

式中的各个占空比根据双电压合成调制策略的原理可以求出，如下所示：

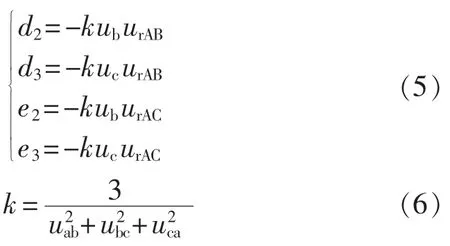
结合MC的拓扑结构，由合成公式知道，输出的A相始终连接在输入的a相上，开关SAa称为原点开关[7]。在合成输出线电压uAB时，只需要在d2Ts时间段内让输出的B相连接到输入的b相上，在d3Ts时间段内让输出的B相连接到输入的c相上，在d1Ts时间段内让输出的B相连接到输入的a相上即可。同样，在合成输出线电压uAC时，只需要在e2Ts时间段内让输出的C相连接到输入的b相上，在e3Ts时间段内让输出的C相连接到输入的c相上，在e1Ts时间段内让输出的C相连接到输入的a相上即可。

3 3×4 MC的双电压控制策略

上述的双电压控制策略可以输出三相对称的线电压，当3×3 MC带平衡负载时，三相负载相电压也是对称的。但是当所带负载为非平衡负载时，负载中性点电位偏移，三相负载相电压不再是对称的。这时可以合理控制3×4 MC的N相桥臂，从而控制负载中性点的电位，使得三相负载相电压为三相对称电压。

为便于从现有的3×3 MC往3×4 MC扩展，本文继承3×3 MC的双电压控制策略，而对中线桥臂进行单独控制。

下面首先分析在双电压控制策略下，输出A、B、C三相桥臂对电源中点O点的电压情况。

仍然假设输入电压在区间2，参考输出电压在区间I，根据上面的原理分析知道，A相桥臂一直连接在输入a相上，由此可以得到：

同样根据调制过程，可以得到B相桥臂对O点的平均电压为：

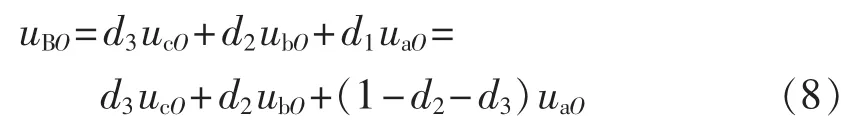
将式（5）代入化简可得：

同样经过分析可以得到C相桥臂对O点的平均电压为：

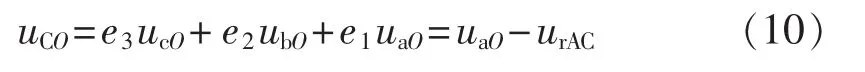
三相桥臂对O点的电压与参考三相负载相电压之差为：

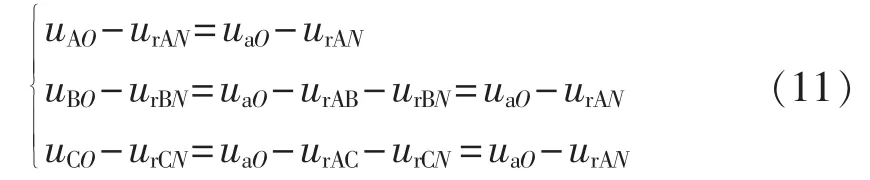
由上式可以看出，这个差值三相是相等的，即三相桥臂对O点的电压中含有零序分量。对于3×4 MC，只需控制N相桥臂，使得负载中性点N对O点电压等于此零序分量，即：

那么实际输出的三相负载相电压即为所希望得到的三相对称电压：

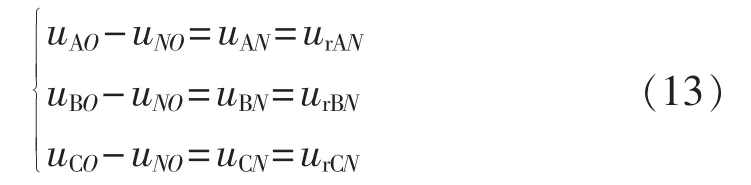
用三相输入相电压来合成N相桥臂输出电压uNO：

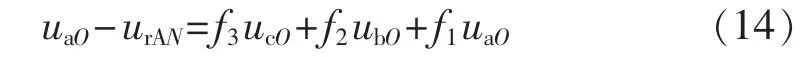
其中， f1、f2、f3分别为输入相电压 uaO、ubO、ucO在合成输出电压uNO中被利用的占空比，并且有如下的关系：

式（14）和（15）可以整理为：

参照文献[17]，令：

代入式（16）得：

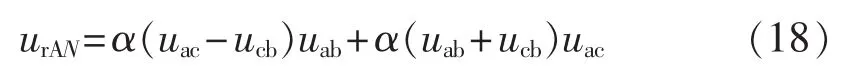
整理、求解可得：

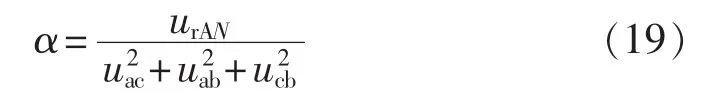
代入式（17）并化简整理可得：

根据上面的推导，在合成输出电压uNO时，只需要在f2Ts时间段内，让输出的N相连接到输入的b相上（即SNb导通)，在f3Ts时间段内，让输出的N相连接到输入的c相上（即SNc导通)，在f1Ts时间段内，让输出的N相连接到输入的a相上（即SNa导通）即可。

同理，可以推导出在其他输入、输出电压区间时的情况。

4 仿真分析

本文基于MATLAB/Simulink和S函数建立了仿真模型，对3×4 MC带不平衡负载和平衡负载情况进行了仿真。仿真参数如下：三相对称输入电压，其相电压峰值为311 V，频率为50 Hz，输出三相电压峰值为269V（最大输出电压），输出电压频率为100Hz；负载1为平衡负载，三相电阻负载，阻值为6 Ω；负载2为不平衡负载，三相电阻负载分别为12、6、8 Ω；输出滤波电感、电容分别为2 mH、24 μF，开关频率为20kHz。仿真结果如图4—6所示。

图4为平衡负载情况下，3×3 MC和3×4 MC的输出电压，两波形形状几乎一样，为三相对称正弦波。这说明在平衡负载情况下，3×4 MC和3×3 MC具有相同的性能。

图5为3×3 MC带不平衡负载时的输出电压和输出电流。三相输出电压波形是不对称的，其中A、B相的电压峰值分别为324、235 V，都远远偏离了参考输出电压，随着负载不平衡的加剧，其电压不对称程度也会加剧，非常不利于负载的运行。

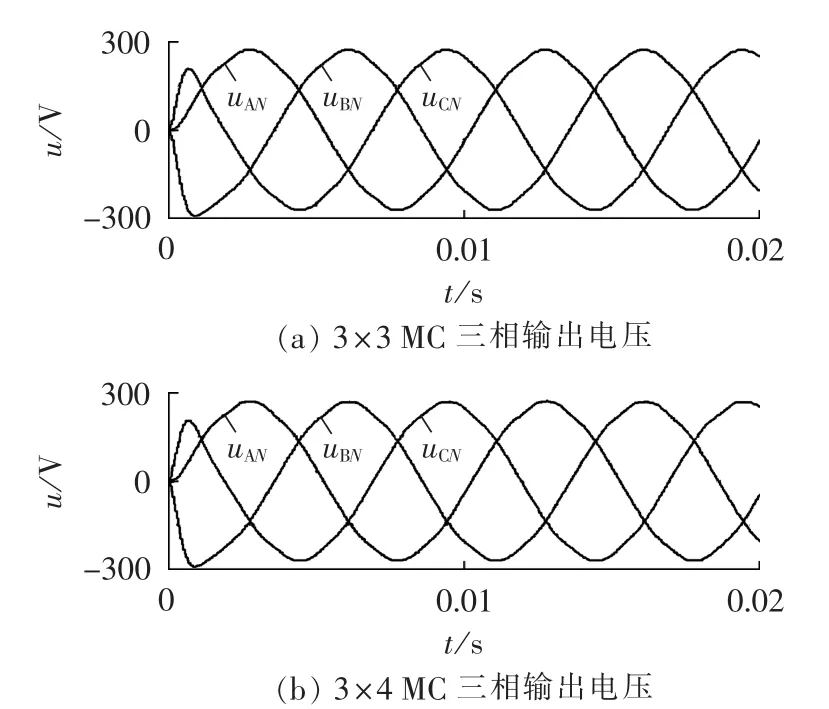
图4 带平衡负载时的仿真结果Fig.4 Simulative result with balance load

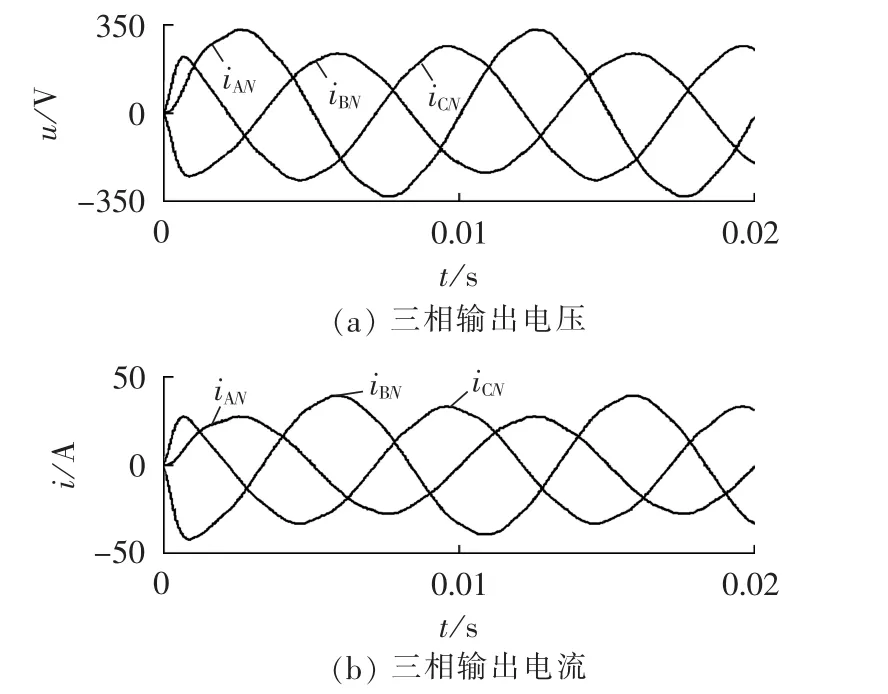
图5 3×3 MC带不平衡负载时的仿真结果Fig.5 Simulative result of 3×3 MC with unbalance load

图6为3×4 MC带不平衡负载时的输出电压和输出电流。经过中线桥臂对负载中性点电压的控制，其三相输出电压基本对称，且幅值接近参考电压幅值，三相幅值分别为271、269、270 V。这说明在不平衡负载情况下，3×4 MC仍然能够为负载提供三相对称的电压，保证各相负载的正常运行。

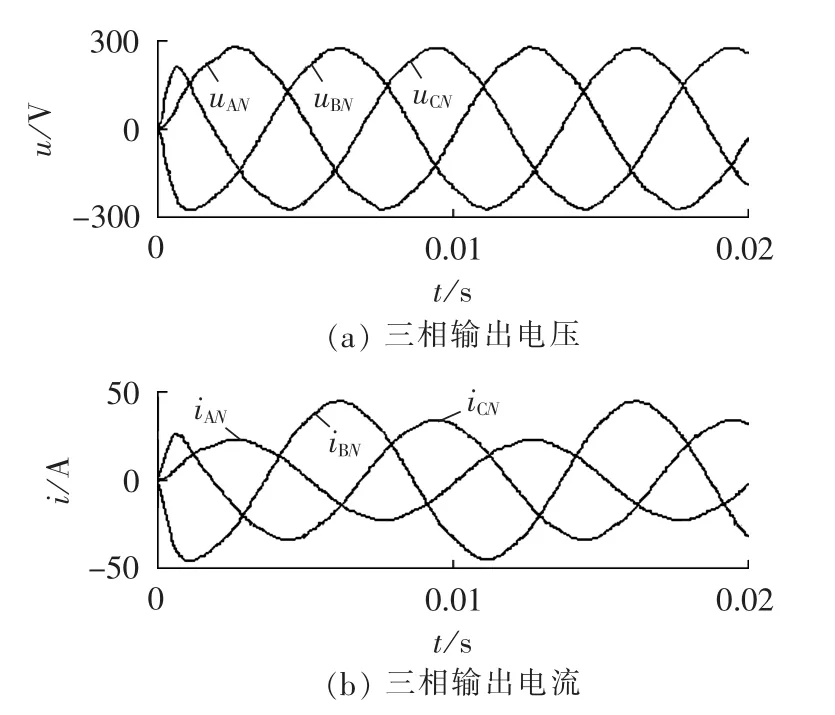
图6 3×4 MC带不平衡负载时的仿真结果Fig.6 Simulative result of 3×4 MC with unbalance load

5 结论

MC具有优越的性能，但是3×3 MC不能带不平衡负载，这限制了MC在实际中的应用。本文应用3×4 MC拓扑结构，对3×4 MC带不平衡负载的情况进行了分析、推导，在此基础上对原3×3 MC部分采用双电压控制，对中线桥臂应用脉宽调制进行单独控制，使在调制方法上对3×3MC具有很好的继承性，便于对现有设备的改造。应用MATLAB/Simulink进行了仿真，仿真结果验证了本文理论分析的正确性。