基于滑窗FFT算法的低频振荡主导模式识别

，

(1.贵阳供电局，贵州 贵阳 550000； 2.清远供电局，广东 清远 511500)

1 引言

电力系统低频振荡的发生机理有待于深入研究[1-3]，因此基于单一机理的振荡模式参数辨识是不准确、不合理的。而直接利用现场实测数据进行低频振荡模式识别分析，则不需要考虑其发生机理和参数模型，是进行电力系统低频振荡主导模式识别的有效方法。目前，基于量测的低频振荡模式识别的方法主要有快速傅里叶算法(FFT)、小波算法、Prony算法、HHT法等。快速傅里叶算法可以通过频谱分析得到信号频率，对含噪信号具有较好鲁棒性，但不能反应振荡的阻尼特性[4]。小波算法通过追踪滑动窗口中的小波脊点的变化反映信号的时变特性，具有较好的抗干扰性[5]，但存在小波基难以选取的问题[6]。Prony算法通过指数函数的多阶线性组合拟合采样信号，反映振荡分量的频率和阻尼[7-9]。但其对噪声非常敏感，降阶模型的研究成为难题[10,11]。HHT算法通过数据的经验模态分解，然后对各固有模态分量进行Hilbert变换，从而提取各振荡参数[12,13]。虽可处理非平稳信号，但其EMD过程可靠性较差，存在着端点效应，过冲现象，难以避免虚假成分，且实时性较差[14]。文献[15-16]提出的基于离散傅里叶的低频振荡分析方法，需要多次人为调整窗口长度，以准确识别频率值，计算量较大，过程较为繁琐；文献[17-18]采用神经网络求解低频振荡模式参数，利用递推最小二乘法进行权值训练，具有较好的抗噪性，但收敛速度受初始权值设置的影响较大。

本文提出了基于滑窗FFT算法的主导模式识别方法。通过对滑窗前后相应谱分量变化的分析，即可求解振荡模式的阻尼特性；只需经过两次快速傅里叶变换，即可较为准确的求解低频振荡的模态参数。并针对FFT算法特有的栅栏效应现象，提出了相应的模式识别方法和步骤。仿真算例中，单模式、多模式低频振荡信号分别在无噪和叠加信噪比为15dB的随机白噪声的情况下进行了识别分析，并与Prony法分析结果进行比较。

2 加窗低频振荡信号的频谱分析

低频振荡信号可以看作频率固定、幅值按指数规律变化的正弦信号的线性组合，则在不考虑噪声的情况下，角频率为ωm，幅值为A，初相为φ，衰减为σ的低频振荡信号可表示为：

x(t)=Ae-σtcos(ωmt+φ)

(1)

由欧拉公式

ejωt=cos(ωt)+jsin(ωt)

(2)

该低频振荡信号可表示为

(3)

经过变换可得

(4)

令

E(ω)=F[e-σt]

(5)

可知低频振荡信号x(t)的傅里叶变换为

(6)

在以上的分析中，低频振荡信号的傅里叶变换是针对整个时域信号进行的，而实际工程中应用的FFT算法只能对有限长度的信号进行分析，而有限长度的信号相当于无限长信号与矩形窗信号在时域上乘积。

设长度为T的矩形窗函数为g(t)，如式(7)所示

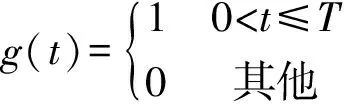
(7)

(8)

其中，d为矩形窗起点。

同理令

GE(ω)=F[g(t-d)e-σt]

(9)

(10)

3 基于滑窗FFT算法的主导模式识别分析

(11)

如果时间长度T取较大值，则可以忽略负频率点处频峰的旁瓣对正频率幅值的影响，也可以忽略频率之间的泄漏影响，即:

(12)

则幅度谱分布为

(13)

因为

(14)

将上式代入式(13)，可得

(15)

相位分布为

(16)

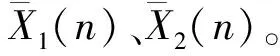
(1)如果k为整数，峰值频率正好位于离散谱线频点上，则角频率为

(17)

由式(15)可知

(18)

由上式可求出阻尼

(19)

由式(15)可知

(20)

由上式可求出幅值

(21)

由式(16)可求出相角为

(22)

(2)峰值频率很难正好落在离散谱线频点上,从而造成栅栏现象。当k不是整数时，设k=k1+r(其中k1为整数，而0

由式(15)可知

(23)

由上式可求出低频振荡信号的阻尼

(24)

由式(15)可知

(25)

将阻尼代入上式可求出参数r，则可求出低频振荡的角频率

(26)

由式(15)可求出低频振荡的幅值

(27)

由式(16)可求出低频振荡信号的相角

(28)

4 仿真算例分析

3.1 单模式低频振荡信号的识别

设电力系统低频振荡信号由1种模式组成，如图1所示。该信号的表达式为

x(t)=0.5e(-0.04t)cos(2π×1.02t-π/6)

取窗口宽度T=20s，采样频率fs=128Hz，采样点数N=2560点，第一次窗口开始时间图t1=0，第二次窗口开始时间图t2=10，进行FFT算法主导模式识别分析。

图2为加15%白噪声后信号。表1为FFT算法的识别结果。表2为加15%白噪声后FFT算法识别结果(表中Prony法识别结果仅列出相匹配模式)。

由表1可知，在无噪情况下，本算法结果较为准确，误差较小。由表2可知，在白噪声的干扰下，Prony算法识别结果中阻尼和幅值都出现了较大误差，而且出现了多余的振荡模式；而本算法识别结果几乎不受影响，抗噪声性较好。

该算例表明了本算法在分析单模式信号的有效性，对噪声具有较好的鲁棒性。

图1 信号振荡曲线

图2 加噪后信号波形

表1加噪前本算法的识别结果

频率/Hz衰减幅值相位/rad真实值1.0200-0.04000.5000-0.5233本算法1.0197-0.04050.4986-0.5339

表2 加噪后两种算法的识别结果

3.2 多模式低频振荡信号的识别

设电力系统低频振荡信号由2种模式组成，如图3所示。该信号的表达式为

x(t)=0.6e-0.02tcos(2π×0.4050t-π/4)+0.7e-0.01tcos(2π×1.5320t-π/3)

取窗口宽度T=50s，采样频率fs=128Hz，采样点数N=6400点，第一次窗口开始时间图t1=0，第二次窗口开始时间图t2=20，进行FFT算法主导模式识别分析。图4为加15%白噪声后信号。表3为FFT算法的识别结果。表4为加15%白噪声后FFT算法识别结果。表5为加15%白噪声后Prony法分析结果(表中仅列出相匹配模式)。

由表3、4可知，在无噪声和叠加白噪声的情况下，基于FFT的识别方法识别结果变化不大，都较为准确；由表5可知，Prony算法识别结果中阻尼和幅值都出现了较大误差，而且出现了多余的振荡模式，给主导模式的筛选带来困难。该算例表明了本算法在分析多模式信号的有效性，且具有较好的抗噪性。

图3 信号振荡曲线

图4 加噪后信号波形

表3加噪前本算法的识别结果

模式频率/Hz衰减幅值相位/rad10.40480.01980.6020-0.754121.53200.01010.7010-1.0580

表4 加噪后本算法的识别结果

表5 加噪后Prony法的识别结果

5 小结

(1) 在分析了低频振荡信号的频谱特性的基础上，推导了加窗低频振荡信号的频谱分布，提出了基于滑窗FFT算法的主导模式识别方法。

(2) 该方法通过固定窗口的滑动，经过相应谱分量的幅值变化进行比较分析，能识别出模式的衰减特性；并针对FFT算法特有的栅栏效应现象，即频率对准与否两种情况进行分析，分别提出了相应的模式识别方法和步骤。仿真结果表明，该方法可以有效的识别低频振荡特征各参数，对随机白噪声的具有较好的鲁棒性，在电力系统低频振荡动态识别中有着积极意义。

[1] 薛禹胜，郝思鹏，刘俊勇.关于低频振荡分析方法的评述[J].电力系统自动化，2009，33(3)：1-8.

[2] Kimoton K A，Kanishia N A，Myamaik T O.Instability of inter-area oscillation mode by auto-parametric resonance[J].IEEE Transations on Power Systems，2004，19(4)：1961-1970.

[3] 陆超，陆秋瑜.电力系统低频振荡模式的自动分类研究[J].电力系统保护与控制，2010，38(4)：35-38.

[4]T.Hiyama,N.Suzuki,T.Funakoshi.On-line Identification of Power System Oscillation Modes By Using Real Time FFT[C].IEEE PES Winter Meeting,Singapore,2000.

[5] 张鹏飞,薛禹胜,张启平.电力系统时变振荡特性的小波脊分析[J].电力系统自动化,2004,28(16):32-35,66.

[6] 穆钢,王宇庭,安军,等.根据受扰轨迹识别电力系统主要振荡模式的信号能量法[J].中国电机工程学报,2007,27(19):7-11.

[7] 王辉,苏小林.Prony 算法的若干改进及其在低频振荡监测中的应用[J].电力系统保护与控制,2011,39(12):140-145.

[8] 马燕峰，赵书强，刘森，等.基于改进多信号Prony算法的低频振荡在线辨识[J].电网技术，2007，31(15)：44-50.

[9] 徐东杰，贺仁睦，高海龙.基于迭代Prony算法的传递函数辨识[J].中国电机工程学报，2004，24(6)：40-43.

[10] 赵礼杰.基于EMD的Prony算法在低频振荡模态参数辨识中的应用[J].电力系统保护与控制,2009,37(23):9-14.

[11] 竺炜,唐颖杰,周有庆,等.基于改进Prony 算法的电力系统低频振荡模式识别[J].电网技术,2009,33(5):44-47.

[12] 李天云，谢家安，张方彦，等.HHT的电力系统低频振荡模态参数提取中的应用[J].中国电机工程学报，2007，27(28)：79-83,29.[13] 韩松，何利铨.孙斌，等.基于希尔伯特一黄变换的电力系统低频振荡的非线性非平稳分析及其应用[J].电网技术，2008，32(4)：56-60.

[14] 穆钢，史坤鹏，安军，等.结合经验模态分解的信号能量法及其在低频振荡研究中的应用[J].中国电机工程学报，2008，28(19)：36-41.

[15] K.Poon and K. Lee.Analysis of transient swings in large interconnected power systems by Fourier transformation[J].IEEE Trans. Power Syst，vol. 3，pp.1573-1579，Nov.1988.148-153，Feb.1990.

[16] P.O′Shea.The use of sliding spectral windows for parameter estimation in power system disturbance monitoring[J].IEEE Trans. Power Syst.，vol. 15，pp.1261-1267，Nov,2000.

[17] 马建伟，竺炜，曾喆昭，等.FFT结合神经网络的低频振荡主导模式识别[J].电力科学与技术学报,2011，26(4)：88-93.

[18] 竺炜，马建伟，曾喆昭，等.分段傅里叶神经网络的低频振荡模式识别方法[J].电力系统保护与控制,2012，40(15)：40-45.