带次优无偏噪声估值器的KF短期负荷预测

，，，，,2

(1.三峡大学 电气与新能源学院，湖北 宜昌 443002；2.国家电网直流建设分公司 ，北京 100052)

1 引言

卡尔曼滤波算法是R.E.Kalman于1960年提出的适合数字计算机的递推滤波方法，它采用状态方程和量测方程组成的状态空间来描述滤波器，该方法所研究的信号过程除了可以是平稳的纯量随机过程，也可包括非平稳的向量随机过程。本文将所有引起负荷变化的因素(如气候、降雨、温度)归为随机系统的随机因素来处理；为了对噪声协方差有比较准确的估计，运用时变次优无偏噪声估值器对噪声协方差进行自适应估计，提高了滤波预测精度。用实际数据进行Matlab仿真验证的结果表明，该方法使误差得到了有效控制。

卡尔曼滤波是基于最小均方误差地递推预测算法，通过对模型参数的辨识，实现对观测序列的预测。其用于负荷预测算法的指导思想是：将负荷分为确定分量和随机分量，确定分量一般采用线性回归模型预测，随机分量采用卡尔曼滤波算法预测。文献[2]较早地将随机系统状态模型辨识技术用于电力系统负荷预报；文献[3]提出了用卡尔曼滤波结合最小二乘法线性拟合及3次样条插值的数学方法；文献[4]提出了自校正移动窗卡尔曼滤波-最小二乘算法，该算法通过移动窗最小二乘算法得到较精确的参数估计；文献[5]则根据对测量新息做出估计，实现了一步预测基础上的二次修正；文献[6]分别以负荷需求序列和时变参数序列为状态变量建立了两个状态空间模型，采用两段自适应卡尔曼滤波方法进行负荷预测；文献[7]提出了在预测值的基础上加上温度修正值的负荷预测方法。

2 卡尔曼滤波理论简介

假设有如下的自由状态定常线性系统模型。

(1)

z(k)=Hx(k)+v(k)

(2)

当系统的初始状态x(k0)及系统干扰ω(k)和测量噪声v(k)是随机过程，为了使问题简化，需要对系统干扰、测量噪声及系统的初始状态作一定的假设。系统干扰和测量噪声是零均值或非零均值的白噪声过程或高斯白噪声过程，即

(3)

式中，Q(k)非负定矩阵，是ω(k)的强度函数；R(k)为对称正定矩阵，是v(k)的方差强度矩阵；d(k)是狄拉克函数；A是n×n维状态转移矩阵；H是1×n维测量矩阵。系统干扰和测量噪声互不相关，且与初始状态x(k0)无关

Cov[ω(k),v(k)]=0

Cov[x(k0),ω(k)]=0

Cov[x(k0),v(k)]=0

(4)

利用正交投影定理推导卡尔曼滤波递推公式如下：

状态预测方程：

(5)

误差协方差预

Pk|k-1=APk-1AT+Qk-1

(6)

状态估计校正：

(7)

误差协方差估计校正：

Pk|k=(I-KkHk)Pk|k-1

(8)

卡尔曼增益：

(9)

详细推导过程见文献[8]。

3 次优无偏估值器的应用改进

为尽量减少随机噪声因素对预测结果的影响，在利用观测数据进行递推滤波的同时，需要不断了不断地修正模型中噪声协方差阵，以提高滤波精度。

确定系统干扰ω(k)、v(k)统计特性，也就是噪声强度矩阵Q(k)、R(k)的确定。Q(k)、R(k)选取好坏对滤波精度有直接的影响，动态模型越不精确，这种影响就越大。但在实际应用中，通过已知信息很难得到比较准确的Q、R值，况且随着新息的不断加入，Q、R值的不准确性越来越明显，这样就直接导致了预测结果偏差比较大。

因此，在对递推方程(6)、(9)进行计算时，有必要对噪声协方差采取自适应的方法，引入次优无偏噪声估值器[9]。

(10)

(11)

以上运用次优无偏估值器计算简单，可同时在线估计出系统噪声协方差和测量噪声协方差，但是在ε(k+1)出现较大值或系统阶数较高时，滤波器易发散。

(12)

(13)

4 算例分析

本文以某实际电网2011年夏季8月7日至15日每天24小时的负荷作为历史负荷。历史负荷曲线见图1，抽离平均值后的随机负荷频数直方图见图2。从图1可见日负荷曲线虽然呈较强的非线性，但是也有明显的以天为周期的周期性，且峰谷负荷出现在固定的时间段。从图2可见随机负荷服从正太分布。

在进行数据分析前先要对异常数据进行处理，再用上文所述方法进行仿真预测。

图1 历史负荷曲线图

图2 随机负荷频数直方图

4.1 模型参数辨识

4.1.1 模型阶数辨识

设已知被辨识系统的随机负荷序列l0,l1,…,lN。并按下式构造Hankel矩阵(简称H矩阵)。

(14)

其维数为m×m。在弱噪声情况下，可分别令m=1,2,3,…，求出每个m值下H阵行列式值，当行列式值达到极大时的m值，即为系统的阶数n；在强噪声情况下，不能直接用随机负荷序列，而是采用随机负荷序列的自相关系数构造H矩阵，即用随机负荷序列的自相关系数ρi代替li，然后计算H阵的行阵式的值，当行阵式值取极小值时的m即为系统阶数[9]。

4.1.2 模型转移矩阵和测量矩阵的辨识

本文采用相关函数——最小二乘相结合的方法辨识系统模型的转移矩阵。基本思想是把辨识分两步进行。第一步，利用相关函数法对随机负荷分量进行一次相关分析，获得被辨识对象的相关函数；第二步利用最小二乘法进一步估计模型的参数。

状态转移矩阵A、测量矩阵H采用与其等价的，辨识参数最少的典范性[2]。

H=[1 0 … 0]1×n

输出随机负荷序列的相关函数为：

R(n)=E{Z(k+n)Z(k)}

(15)

根据平稳过程遍历性，统计均值可以用时间平均代替，(15)式可改写为：

(16)

可以推得(16)式的递推式为：

(17)

式子中ak为A中第一行参数，利用(16)、(17)式，采用最小二乘法即可计算出模型参数ak的值。

4.2 算法步骤

(1)分析历史负荷数据，处理异常数据点。

(2)根据4.1求模型参数，模型参数及递推初始值见表1。

表1 模型参数

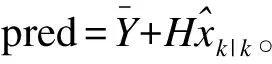
4.3 仿真结果

下面给出利用上述方法得到的预测误差和预测结果，预测相对误差见图3，预测结果对比见图4。为了衡量负荷预测的有效性用百分相对误差(Relative Percentage Error ，RPE)来计算某一时刻的误差，用平均绝对百分误差(Mean Absolute Percentage Error,MAPE)来反映误差总体大小。其计算式如下：

(18)

(19)

图3 相对误差图

图4 负荷对比图

其平均相对误差为-0.38%，平均绝对误差为1.24%。由此可见对次优无偏噪声估值器的应用改进是有效的。

5 结论

本文运用带次优无偏噪声估值器的卡尔曼滤波理论建立了短期负荷预测模型，并进行短期负荷预测。通过Matlab仿真计算证明了该预测模型的可行性。同时针对负荷预测的特点，通过对次优无偏噪声估值器的改进，提高了预测精度。

参数辨识后的带次优无偏估值器的卡尔曼滤波器始终处于稳定状态，说明卡尔曼滤波模型参数辨识方法是可行的。

另外，将其他影响负荷的因素(如温度，降雨，体感温度)等与本文的方法综合考虑，可期望得到更好的预测结果。

[1] P.C.Gupta,K.Yamada.Adaptive short-term forecasting of hourly loads usingweather information[J],IEEE Transactions powerApparatusSystem,PAS-91,1972:2085-2094.

[2] 李洪心，易允文.随机辨识系统在电力系统负荷预报中的应用[J].信息与控制，1985(3):31-34.

[3] 张民，鲍海，晏玲，等.基于卡尔曼滤波的短期负荷预测方法的研究[J].电网技术，2003,27(10)：39-42.

[4] 王正欧，张建平，等.电力系统超短期负荷预报的一种方法[J].天津大学学报，1992(2)：125-130.

[5] 孟思齐，杨洪耕.基于卡尔曼滤波二次修正的短期负荷预测[J]，电网与水力发电进展,2008,24(2)：78-82.

[6] 马静波，杨洪耕.自适应卡尔曼滤波在电力系统短期负荷预测中的应用[J].电网技术，2005,29(1)：75-79.

[7] 李明干，孙健利，刘沛.基于卡尔曼滤波的电力系统短期负荷预测[J].继电器，2004,32(4)：9-12.

[8] 王志贤.最优状态估计与系统辨识[M].西安：西北工业大学出版社，2004.

[9] 刘胜，张红梅.最优估计理论[M].北京：科学出版社，2011.