基于精确线性化算法的TCR-TSC型SVC控制器设计

，，

(西南交通大学电气工程学院,四川 成都 610031)

1 引言

静止无功补偿器(Static VAR Compensator，简称SVC)是目前电力系统中应用最多，最为成熟的并联补偿设备，也是一类最早的到实际应用的FACTS控制器。其最基本的特点就是可以连续调节从电网吸收或者向电网传送的无功功率，从而有效的维持SVC装置安置点的电压在电力系统处于小干扰和大干扰下的稳定性，有利于改善电力系统的电压质量，同时也有效的维持了电力系统的无功功率平衡。

随着现代电力电子技术的发展，SVC在电力系统中的应用越来越广泛，相对于传统的电容器并联投切技术而言，SVC具有突出的控制快速性和高效性，因此，进一步深入研究SVC的控制规律对提高SVC在电力系统稳定性中发挥更大的作用有重要意义。

电力系统以及在电力系统中应用的各种FACTS装置本质上都是非线性系统，而处理这样的非线性系统传统的控制方法主要是：单变量反馈控制[1]、自适应控制[2]、辅助控制[3]及线性最优控制[4]等。但它们在系统的稳定运行点发生较大范围的变化时，控制器的控制效果会出现性能恶化，而本文是针对于电力系统这种典型的仿射非线性系统采用了基于状态反馈精确线性化的设计原理进行非线性控制器的设计，可以有效解决这个问题。文献[5]是利用状态反馈精确线性化原理对TCR-FC型SVC系统进行间接设计，本文将在此基础之上对更复杂的TCR-TSC型SVC系统进行设计，这种SVC的总导纳具有更大的调节范围，并且直接对晶闸管的导通角进行动态控制，实用性和目的性更强。

以下将对TCR-TSC型SVC控制系统建立仿射非线性模型[6]，并且采用状态反馈精确线性化设计原理设计出这种SVC的非线性控制器，通过对单机无穷大系统的大扰动仿真，验证了这种非线性控制器有较好的控制作用。

2 TCR-TSC型SVC的结构及其数学模型

TCR-TSC型SVC的单相结构如图1所示，根据装置容量、谐波影响、晶闸管阀参数、成本等而由m条TCR支路和n条TSC支路(或者容性滤波器支路)构成，图中m=1，n=3。

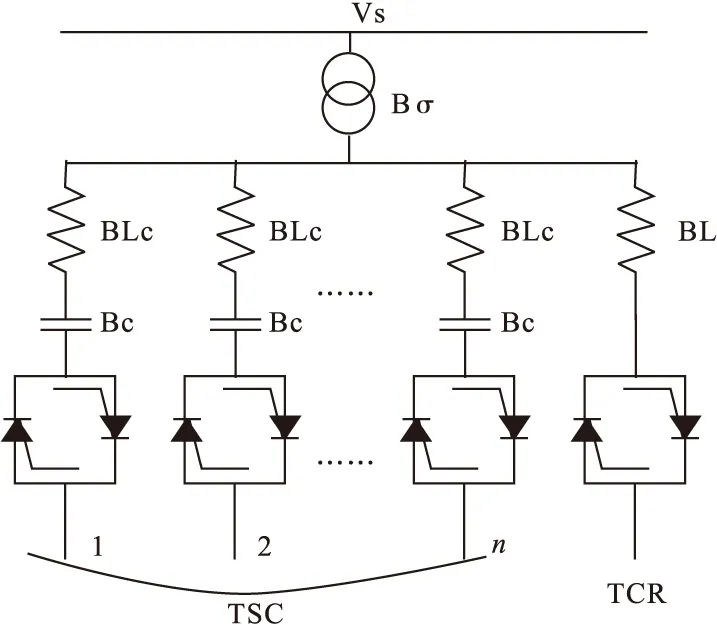
图1 TCR-TSC型SVC单相结构图

在图1中，对于由一个TCR装置和n个TSC装置并联而成的SVC补偿装置，可以求出它的总的电纳值为：

(1)

其中，由各个支路可知：

(2)

(3)

式中α是TCR中可控硅的触发角，当α在90°～180°之间连续变化时，BTCR的值可以在0与只见连续变化，而当TSC的支路投切数目n从0到n变化时，可以在0～nBCn之间变化了。因此可以计算出TCR-TSC型SVC补偿装置的最大与最小电纳值分别是：

(4)

(5)

从中也可以看出TCR-TSC型SVC补偿器比TCR-FC型SVC补偿器的导纳有更大的调节范围。

3 基于SVC的单机无穷大系统的数学模型

在单机无穷大的电力系统中接入TCR-TSC型SVC补偿器装置后，其原理接线图和相应的等值电路图2所示。

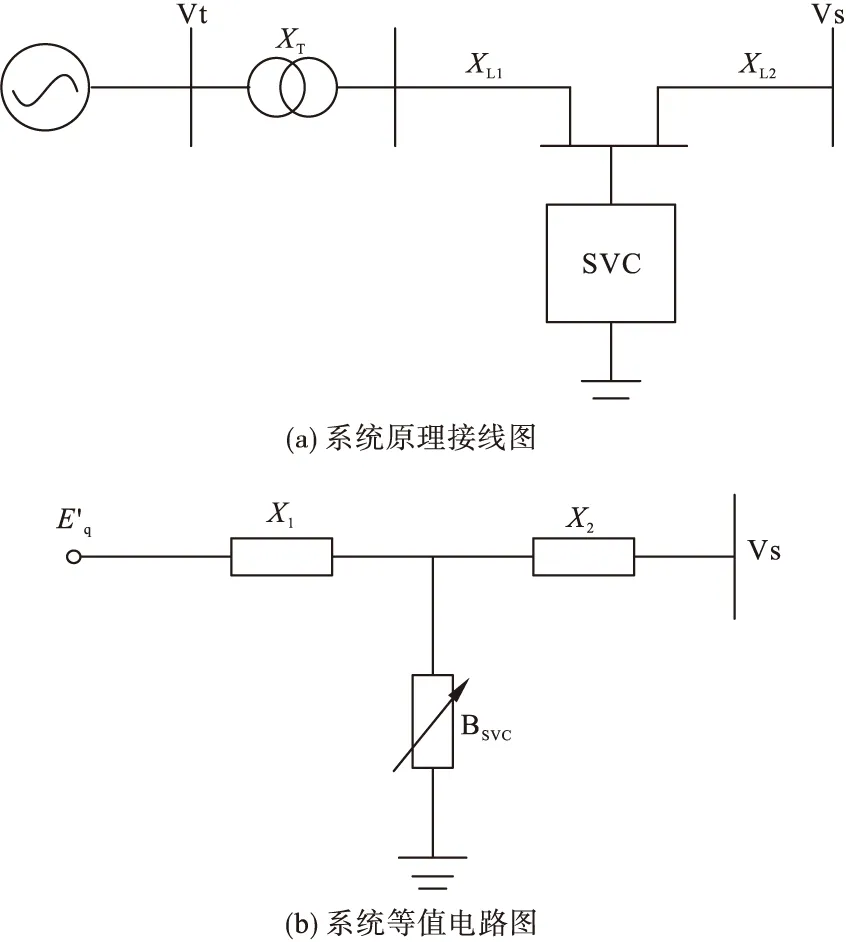
图2 系统原理接线图和等值电路图

通常发电机的转子运动方程式可以写成：

(6)

式中，δ为发电机转子运行角；ω为发电机转子转速；Pm为发电机机械功率；Pe为发电机电功率；H为机组转动惯量；D为阻尼系数。

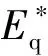
(7)

将式(7)代入到式(6)中则可以得到基于SVC的单机无穷大系统的非线性状态方程式：

(8)

式中，δ(t)和ω(t)为系统的两个状态变量；BSVC为系统输入控制变量。为了建立仿射非线性系统的形式：

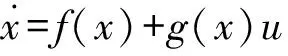
(9)

将令输入控制变量u为：

(10)

则(6)式所描述的基于SVC的无穷大系统的仿射非线性模型为：

(11)

4 SVC的非线性最优控制器设计

由文献[5]可知，对于仿射非线性系统的可精确线性化的条件是矩阵

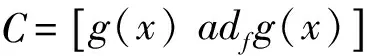
在x0点的邻域Ω内是非奇异矩阵。

对于(11)式所构建的仿射非线性模型计算g(x)对于f(x)的Lie括号可得：

从而可得：

C=

由此可以计算出C矩阵的行列式值为：

显然在邻域Ω={δ| 0°<δ<180°}内，det(C)≠0。从而在δ∈(0°,180°)内此仿射非线性系统可以进行精确线性化的。

根据文献[5]的状态反馈精确线性化算法流程，可以将式(11)所描述的仿射非线性变换为一个完全可控的线性系统：

(12)

以及原非线性系统的控制律：

(13)

其中：

在算法中最后选择的坐标变换是：

(14)

对于式(12)所描述的完全可控线性系统，根据二次型性能指标的线性最优控制设计方法(LQR方法)[7]可知，使得性能指标泛函J[5]达到极值的预控制向量v*为：

v*=-k1z1-k2z2

(15)

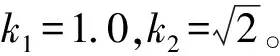
最后可得到在性能指标：

(16)

取最小极值，即转子角偏差和电磁功率振荡最小时；原系统(11)的非线性控制规律为：

(17)

由式(10)中所表示的BSVC与输入控制量u之间的关系可以得到：

(18)

式(18)为最终得到的基于SVC补偿器的单机无穷大系统的控制律。

由式(1)～(3)所描述的TCR-TSC型SVC补偿器数学模型可得：

(19)

由以上的分析可以得到TCR-TSC型SVC补偿器的非线性最优控制器的实现框图如图3所示。

5 系统仿真

为检验上述非线性控制方法的控制效果，下面对如图3所示的具有TCR-TSC型SVC补偿器的单机无穷大电力系统进行MATLAB仿真，并将非线性控制方法的仿真效果与常规的线性最优控制方法仿真效果进行对比。

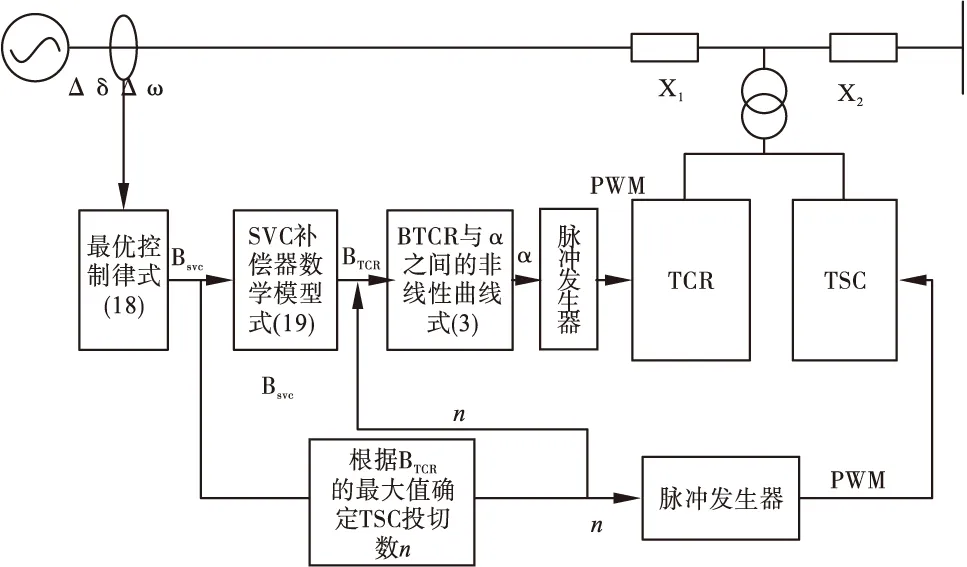
图3 最优控制器系统的实现框图

此次仿真中，TCR-TSC型SVC补偿装置是由一条TCR支路和三条TSC支路构成。确定系统的各部分参数如下：

发电机处变压器以及线路参数：XT=0.1，XL1=0.2，XL2=0.2；

TCR-TSC型SVC参数：Bσ=-4.2，BL=-0.673，BLC=-0.044，BC=0.00308。

令系统中：Pm=1.0，Vs=1.0。

分别在以下两种故障下进行仿真：

①系统受到小干扰：在t=2s时，发电机输出电压增大5%；在t=5s时，发电机输出电压减小4%；

系统在这种小干扰下SVC装置处的电压以及SVC吸收的无功功率为图4所示。

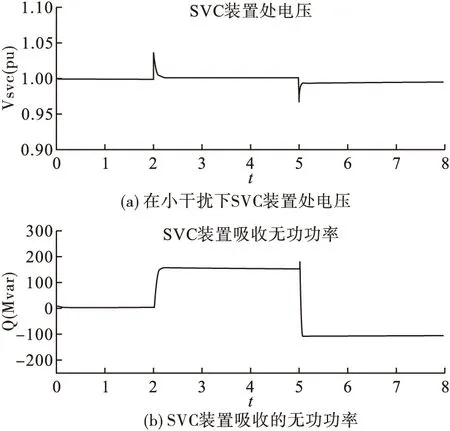
图4 SVC装置处电压以及所吸收的无功功率仿真图

②系统受到大干扰：在t=0s时，发电机高压侧母线发生三相短路故障，t=0.2s时故障切除。在这种大扰动情况下，将本此设计的非线性最优控制器的控制效果与常规线性最优控制器[5]控制效果进行对比，结果如图5所示。

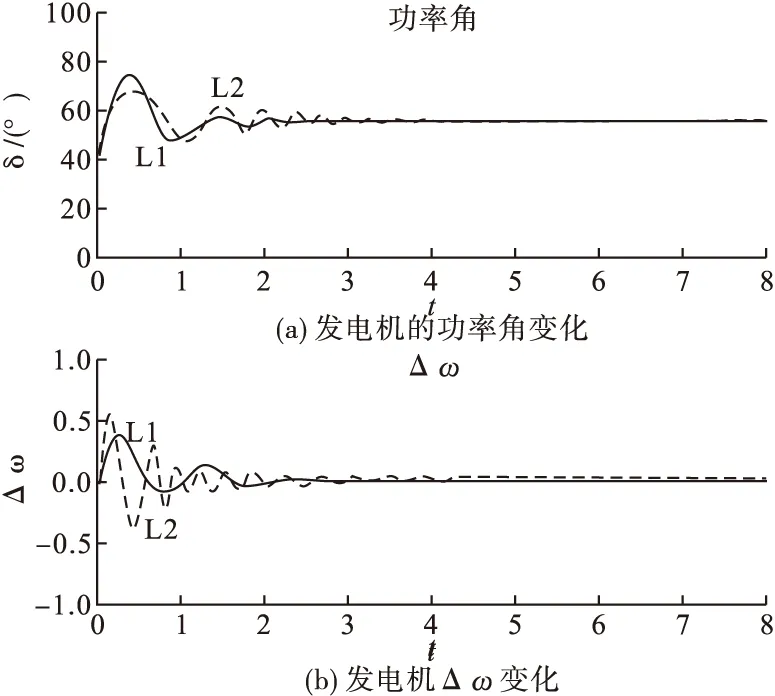
L1：非线性最优控制器控制效果 L2：常规线性最优控制器控制效果

从图5中可以看出，在系统处于大扰动下，不论是发电机的功率角响应，还是发电机Δω响应，显然在本次所设计的非线性最优控制器控制下，系统总能在较快的时间下趋于稳定，因此改善了电力系统在大扰动下的的暂态稳定性。

6 结论

从系统的最终仿真效果可以得出，基于精确线性化算法所设计的非线性最优控制器最大的优点就是系统在处于大扰动下，其频率和功角振荡较小，能在很短的时间内会到原来的平衡状态。从而验证了本次设计的非线性最优控制器具有较好的控制效果。

[1] Kapoor S C.Dynamic Stability of Long Transmission Systems with Static Compensators and Synchronous Machines.IEEETrans on PAS,1979,98(1):124-134.

[2] Dash P K,Sharaf A M,Hill E F.An Adaptive Stabilizer for Thyristor Controlled Static VAR Compensators for Power Systems.IEEE Trans on Power Systems,1989,4(2):403-410.

[3] Wu C J,Lee Y S.Damping of Synchronous Generator by Static Reactive Power Compensator with Digital Controller.IEE Proc-C,1991,138(5).

[4] Brucoli M,Torelli F,Trovato M.A Decentralized Control Strategy for Dynamic Shunt VAR Compensation in Interconnected Power Systems.IEE Proc-C,1985,132(5).

[5] 卢 强,孙元章.电力系统非线性控制(Nonlinear Control for Power System)[M].北京:科学出版社(Beijing:Science Press),1993.

[6] 丁青青,王赞基.TCR-TSC 型 SVC 的非仿射非线性控制器设计[J].电力系统自动化,2002,26(14):12-15.

[7] Kwakernak H,Sivan R.Linear Optimal Control Systems.New York:Wiley,1972.