EHV输电线路上潜供电弧的分布参数计算模型探讨

，，，，

(广西大学电气工程学院，广西 南宁 530004)

1 引言

潜供电弧是针对330kV及以上电压等级的输电线路单相接地故障而言的，在220kV及以下各电压等级的线路上，运行经验、计算均表明，在故障点处的对地弧光都能在约0.2s内快速自行熄灭，没有持续燃烧的现象，不存在潜供电弧[2]。而在330kV及以上电压等级的线路上，在故障点处的对地弧光不能快速自灭(超过0.2～0.3s)，系统中短路点仍然存在，断路器重合闸后，系统继续接地，重合闸失效，这是因为数安或数十安的潜供电流存在于短路点和大地之间，导致重合闸失败。当单相接地故障发生后，超高压输电线路故障相线路两端断路器跳开，在故障位置处弧光中的短路电流被切断，弧光本应随即自灭，弧道的介质强度本应快速地恢复起来，但由于非故障相通过相间电容和相间互感对故障相进行容性和感性供电[1]。因此，虽然高达数千安的短路电流已经被切断，但在弧光的通道中仍然残留有数安、数十安的剩余持续电流，这就是“潜供电流”；潜供电流使弧光持续燃烧，称之为“潜供电弧”，当这一弧光在空间游动自灭后，故障相全线路上残留有一定的电压，这就是“潜供电弧的恢复电压”[3]。潜供电流和恢复电压在故障相线路上都具有一定的分布特性，需进行分布参数计算模型的探讨。

2 不带任何补偿装置的超高压输电线路潜供电弧分布参数计算模型

2.1 模型假设

这里为了计算的方便，做了如下的模型假设：①忽略非故障相的对地电容，其对潜供电弧的计算没什么影响；②忽略故障相的沿线有功电阻；③略去全部对地有功泄漏。另外，假设输电线路的基本参数如下：线路自感系数为L，线间互感系数为M；线路对地电容C0，线间电容C1(均以单位长计算，例如每公里的数值)。这些参数沿线路是分布性的，因此潜供电弧参数在断开相上也具有分布特性。

2.2 通过线路单元等值回路图建立数学模型

依据模型假设，可以建立线路单元等值回路图，如图1所示。

图1 线路单元等值图

其中，l(公里)是线路长度；ω=2πf=314。令

再令C=2C1，由此可以得到：

如此可以将线路单元等值回路简化成如图2所示的形式，求解(5)、(6)可以得到：

(7)

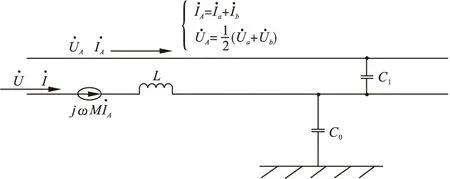
图2 简化的等值线路

(8)

再将(6)式带进(8)式可以得到式(9)：

(9)

上式方程的全解如下[4，5]：

因此全解为：

2.2.1 恢复电压数学模型

(16)

联合(14)、(15)、(16)三式，得到：

为了计算时减小误差，考虑：

(17)

2.2.2 潜供电流数学模型

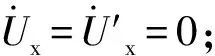
(18)

(19)

由上两式可得：

(20)

(21)

因此，弧道处的电流为：

(22)

4 装有串联补偿装置和电抗器的输电线路上潜供电弧分布参数计算模型

超高压输电线路上常设有串联电容和并联电抗，它们的位置或在首端，或在末端，或在中点，假设在线路首末两端都装有电抗器和串联补偿站，线路中间装有串联补偿站，其接线方式如图3所示。

线路上各参数的计算如下：

公式(12)、(13)所表示的全解在这里同样适用，只是边界条件不一样了。根据上图可以将线路分为两部分：其一，短路发生在0～l′之间；其二，短路发生在l′～l之间。这里先求0～l′的情况。

图3 超高压线路简化图

(23)

其中：

4.1 恢复电压分布参数模型的推导

在推导潜供电弧的恢复电压公式中，为了简化计算，忽略了各串联补偿电容器上当潜供电弧熄灭时所残存的电荷的影响[2]。当潜供电弧熄灭的瞬间，即潜供电流过零中断，此时，在故障相的各电容站上的电压正好达到极大值，有一些串联补偿站并联有释能元件，此电荷随即消失；另有一些串联补偿站没有并联释能元件，但整条线路自两端经并联电抗接地，电容上的电荷总会自行消失(这需要一定的时间)，我们的目的是求得潜供电弧恢复电压的稳态数值，因此，各电容站上的残存电荷略去不计。求恢复电压的边界条件如下：

根据之前的分析，将上述边界条件分别带入全解(12)、(13)式中可得以下六个方程：

(25)

(26)

(27)

(28)

(29)

(30)

联立以上六个方程可得：

(31)

其中：

4.2 弧道中潜供电流公式的推导

依据之前的方法，同理可得：

(32)

其中：

当单相接地故障发生在l′～l之间时，依据以上的分析，同理可以得到如下的结果：l′～l之间潜供电流的沿线分布：

(33)

l′～l之间弧道恢复电压的沿线分布：

(34)

(35)

化简得到：

(36)

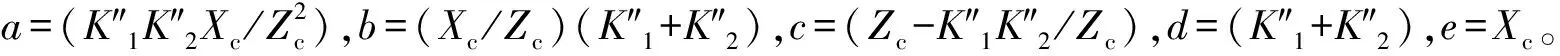
(37)

4.3 模型分析

线路上装设并联电抗时，不论其中性点采取何种接地方式，在两相运行中都有可能出现电压谐振现象[8，9]，这是由两个非故障相的电压(设系统内阻略去不计)加在下述两个串联的阻抗之上所引起的：一个阻抗是相间电容(或再并上由电抗器中性点对地小阻抗形成的等值相间电抗)；另一个是故障相对地电容，再加上等值的对地电抗。当这两个串联阻抗的入端总内阻抗为零或接近于零时，即使外加电压不天，因这两个阻抗的相位差180°，就有可能在每一阻抗上形成极高的电压，形成电压谐振。产生电压谐振的临界线长为系统参数所定，因此，改变系统参数(包括中性点的小电抗值)也可以改变产生电压谐振的线长。

(38)

5 结语

[1] 牛晓民,王晓彤,等.超高压串联补偿输电线路的潜供电流和恢复电压[J].电网技术，1998,22(9)：10-16.

[2] 曹荣江,末拱照,崔景春.关于超高压线路上潜供电弧持续现象的研究[J].高电压技术,1975，1:34-46.

[3] 柴旭峥,梁曦东,曾嵘,等.串联补偿的远距离输电线路潜供电弧参数特[J].电力系统白动化,2007,31(5):7-12.

[4] 鲁铁成.电力系统过电压[M].北京:水利电力出版社,2009.

[5] Maria Cristina Tavares,Carlos Medeiros Portela.Transmission System Parameters Optimization Sensitivity Analysis of Secondary Arc Current and Recovery Voltage[J].IEEE Transactions On Power Delivery,2004,19(3):1464-1471.

[6] 梅忠恕.超高压电网潜供电流和单相重合闸[J].云南电力技术，1999，27(2):9 -11.

[7] 梅忠恕.超高压电网潜供电流与单相重合闸(II)[J].云南电力技术，1999，27(3):15-18.

[8] 鲁炜.超高压输电线路雷电过电压及单相闪络跳闸后潜供电流的研究[D].武汉:武汉大学电气工程学院,2004.

[9] 尹忠东,刘虹.超高压电网可控串联补偿与潜供电弧的抑制[J].高电压技术,1998,24(1):14-16.