自适应变间距直线拟合非圆弧曲线算法

潘应晖，翁本杰，杨东东，魏 攀，刘建东，吴棚业

(武夷学院机电工程学院，福建武夷山354300)

0 前言

目前一般的数控系统只有直线插补和圆弧插补功能[1]，对椭圆、抛物线、双曲线等非圆弧曲线，无法直接利用数控系统内置的插补指令进行加工。根据数学微分原理，通常采用微小直线或圆弧来拟合所需加工的非圆弧曲线，通过控制拟合直线或圆弧的最大偏差小于等于允许偏差，计算出每段直线或圆弧的起点、终点、圆弧半径等参数，利用数控系统宏程序完成加工。

常用的直线拟合方法有等间距法[2]、等弦长法[3]和等误差法[4]等。等间距法是在非圆弧曲线与拟合直线的最大偏差小于允许偏差的条件下,将某一坐标轴或曲线方程中的某一参变量划分成相等的间距，间距值越大,拟合误差越大；等弦长法则是通过使各节点间的弦长相等来拟合，它取决于最小曲率半径,必须使该处满足加工要求。这两种方法的共同特点是：计算方法较为简单，但当非圆弧曲线的曲率变化较大时,由于间距和弦长均为定值,一方面造成被加工零件的表面粗糙度变化较大,另一方面在非圆弧曲线曲率半径较小处产生多个不必要节点,降低加工效率，仅适用于曲率变化较小的非圆弧曲线。等误差直线拟合法是用直线段拟合非圆弧曲线时,使拟合误差始终等于系统允许偏差,因此节点间的线段长度随曲线曲率半径而变化,采用变步长插值。何其宝[5]、于洋等[6]虽提出了等误差直线拟合法数学模型,但在求解高次方程组时,无法得到解析解,很难用于实际加工。赵玉刚等[7]虽提出了非圆弧曲线的加工算法,但需以C++Builder6.0等为开发工具，不能在数控机床上直接应用，在工程上使用受到很大限制。

圆弧拟合有曲率圆法[8]、三点圆法[9]和相切圆法[10，11]、双圆弧法[12]、最小二乘法[13,14]、等弧长法[15]等方法。由于这些算法比较复杂,计算参数多,计算量大,拟合效率低,求解困难，一般需先通过VB、VC等开发工具，计算出拟合圆弧的起点、终点、圆弧半径等参数，很难直接使用数控编程指令进行实际编程，因此生产中广泛采用直线拟合零件非圆弧曲线轮廓的方法。

为克服直线拟合存在的缺陷，作者结合等间距法、等弦长法和等误差法的优点，提出一种自适应变间距直线拟合非圆弧曲线算法，在拟合直线最大偏差≤允许偏差条件下，能根据非圆弧曲线，快速确定直线拟合的最佳节点，有效提高编程效率和加工精度，满足生产需要。

1 计算模型

假设曲线函数方程X=f(Z),如图1所示。

图1 计算几何关系图

该曲线在A点的坐标为(ZA,XA),由高数知识可求得A点曲率半径RA为

为求下一个节点B(ZB,XB),沿Z轴方向初定一个微小间距△Z,使ZB=ZA+△Z,则XB=f(ZB),用弦线联结A、B两点,弦长AB的长度LAB为

然后求解弦线与曲线在A、B两点间的最大误差δ。由于间距△Z数值很小，误差δ数值则更小,所以可以将过A点和B点的曲线近似为一段圆弧,直线MN为弦AB的垂直平分线，因此最大误差δ即为弦AB的垂直平分线上线段MN长度。由图1直角三角形RT△ANC几何关系可知

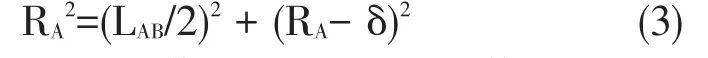
曲率半径RA为正值，最大误差δ数值很小，由（3）式可推导出最大误差δ为

若最大误差δ≤允许偏差δ允,说明A、B两节点用直线拟合时所产生的最大误差在允许范围内，可以采用；若最大误差δ＞允许偏差δ允,直线拟合产生的误差超出允许范围，不允许使用，应该减小间距△Z,直到最大误差δ≤允许偏差δ允。

2 自适应变间距直线拟合非圆弧算法

初定微小间距△Z，步长计数变量初值置为0，根据公式（4）可计算下一节点坐标及其误差δ，若δ≤δ允,保存该点坐标值，步长计数变量加1，继续计算下一间距节点坐标及误差δ，比较δ≤δ允,同理直至δ＞δ允，则该点之前的上一节点就是直线拟合的最佳节点；若δ＞δ允且步长计数变量≤1,说明只进行了一次节点计算，但因间距△Z过大，拟合时超出允许偏差，因此必须减小间距△Z数值,可采用优选学中的黄金分割法进行黄金分割，即用0.618乘间距△Z作为新间距△Z，返回重新计算下一点坐标及其误差δ,继续比较δ、δ允。

起点及最佳节点确定后，进行直线插补，接着以最佳节点为起始点，比较步长计数变量，若该值为4表示通过4次运算才找到最佳节点，为提高计算效率，当该值≥4时，将间距△Z乘以黄金比例1.618，作为新间距△Z,开始下一节点的计算，重复上一过程直到插补完成。其流程图如下：

初始确定的微小间距△Z，一般为允许偏差δ允的二至五倍即可，若所设初值偏大或偏小，对加工的影响也不大，因按图2流程算法进行编程时，系统能自动进行修正。

该算法克服了等间距法、等弦长法和等误差法的缺点，其最佳节点不是按等间距或等弦长确定，而是在最大误差≤允许偏差条件下，根据非圆弧曲线自适应变间距确定。

图2 自适应变间距等误差算法流程图

3 应用实例

已知待加工铝棒毛坯直径为80mm,要加工下图3所示工件，右边为抛物线，其标准方程Z=-CX2(其中C为常数，这里取C=1/15)。现以SINUMER⁃IK 802S数车系统进行加工编程，采用直线插补拟合抛物线，包括粗车和精车，说明非圆弧曲线的编程方法。

图3 加工零件示意图

3.1 编程设置

因数控车床对刀时一般以工件右端面的圆心设为工件坐标原点，根据该抛物线方程的特点，为便于编程计算，且采用半径编程，初始化设置如下：（程序分号“；”后的文字为相应注释）

G90G22G71G94T1D1M03S500F50；初始化设置

G0X30Z200；起刀点

R0=40；毛坯半径

R1=1/15；抛物线系数C

R2=30；抛物线终点X坐标

R3=1；X方向粗车背吃刀量(半径值)

R4=0.5；X方向精车背吃刀量(半径值)

3.2 工艺路线

待加工铝棒毛坯直径为80mm,抛物线曲线加工余量较大，先进行粗加工，采用刀具走直线的方式分段粗车，保留精加工余量，然后精车抛物线曲线外形。

3.3 抛物线曲线粗车路线

采用直线插补，每次粗加工时X方向背吃刀量为R3，走刀路线如图4所示。

图4 抛物线粗车路线示意图

每次直线插补必须确定相应的Z坐标值。当X坐标值大于抛物线终点X坐标时，Z=抛物线终点Z坐标+精加工余量；当X坐标值小于或等于抛物线终点X坐标时可根据抛物线方程，计算出Z坐标值,同时考虑保留精加工余量，因此该次粗加工时Z=-CX2+精加工余量，利用绝对跳转与有条件跳转语句，通过参数编程可实现上述过程的抛物线粗加工。程序如下：

R5=R0-R3；粗车时X坐标数值

BB1:G0 Z=1；粗车时Z轴起始点坐标

X=R5；粗车时X轴起始点坐标

IF R5＞=R2 GOTOF BB2；当X轴坐标大于抛物线终点X轴坐标时，转到BB2

R6=-R1*R5*R5+R4；X轴坐标小于抛物线终点X轴坐标时，Z轴的终点坐标

GOTOF BB3；转到BB3标记处

BB2:R6=-R2*R2*R1+R4；超过抛物线终点X轴坐标时，Z轴的终点坐标

BB3:G1 Z=R6；直线插补粗车

G0 X=R0+1 Z=1；返回粗车起始点

R5=R5-R3；粗车时X轴起始点坐标，即每次粗加工X向背吃刀量为R3

IF R5＞R3 GOTOB BB1；如X向粗加工余量大于R3，返回BB1标记处再粗加工

3.4 抛物线曲线精车路线

已知抛物线方程，利用高数知识，可得出曲率半径及弦长计算公式，根据上述流程图2，可以计算出符合加工精度要求的直线拟合抛物线的最佳节点，因此利用R参数变量及有条件跳转语句，实现抛物线曲线精加工。程序如下：

G0 Z=R1+1 X0；返回精加工起始点

S800F30 G64；连续路径加工

G1 Z=0；直线插补至抛物线起点处

R7=-0.1；计算间距增量△Z

R8=0.05；允许偏差δ允

R15=0；抛物线起始点坐标

R16=0

EEE:R10=R15；每次运算起点坐标

R11=R16

R12=0；步长计数变量

R20=(1-R1*R10)*SQRT(1-R1*R10)*0.5/R1；曲率半径

RRR:R13=R15+R7；下一点坐标

R14=SQRT(-R13/R1)

R12=R12+1；步长计数变量+1

R17=SQRT((R13-R10)*(R13-R10)+(R14-R11)*(R14-R11))；两点弦长

R21=R20-SQRT(R20*R20-R17*R17/4)；最大误差δ

IF R21＞R8 GOTOF TTT；超过允许偏差转到TTT

R15=R13；未超过允许偏差，存储该点坐标，继续计算下一点

R16=R14

GOTOB RRR

TTT:IF R12＞1 GOTOF YYY；步长计数变量超过1次，转到YYY

R7=0.618*R7；间距增量△Z按黄金分割减小

GOTOB RRR

YYY:G01 Z=R15 X=R16；直线插补加工

IF R12＜4 GOTOF UUU；计算次数＜4次

R7=1.618*R7；间距增量△Z按黄金分割增大

UUU:IF R16＜R2 GOTOB EEE

G00 X=50 Z200

M05M02

利用南京斯沃数控6.50版仿真软件，将上述程序导入西门子SINUMERIK 802Se T数车系统，运行后得到的仿真结果如图5所示。

图5 抛物线精加工结果

4 结语

数控机床的使用日益普遍，要充分发挥数控机床的功能，开拓数控机床的使用范围，程序编制是不可忽视的重要环节。本文提供的自适应变间距直线拟合非圆弧曲线算法,避免了高次方程组的求解，运算速度快，容易控制拟合精度，无需任何辅助软件,利用数控系统自身宏程序功能即可直接在数控系统上编程实现非圆弧曲线的数控加工，通用性好，能适用于一般非圆弧曲线，在数控加工中有一定的参考应用价值。

[1]沈纪桂.数控加工圆弧拟合的优化方法[J].机械工程学报，1997，33（6）：65-70.

[2]李明贵.非圆曲面的加工[J].西安石油大学学报:自然科学版，2004，19（2）：54-57.

[3]王学颖，任鹏.数控机床等弦长拟合优化算法的实现[J].沈阳师范大学学报:自然科学版，2010，28（4）：499-502.

[4]蔡永林，席光，孙卫青.一种新的平面曲线圆弧插补节点获取方法[J].工程图学学报，2002，23（1）：97-103.

[5]何其宝.非圆曲线轮廓数控加工编程误差的控制[J].机械制造与自动化，2006，35（5）：72-73,76.

[6]于洋，魏娟.等误差直线逼近非圆曲线节点计算新方法[J].组合机床与自动化加工技术，2005，42（5）：32-33.

[7]赵玉刚，于光伟，张健，等.曲线等误差直线拟合的算法研究及其应用[J].制造技术与机床，2010，53（6）：171-175.

[8]郄胜强，王先逵.变曲率对称圆弧曲线及其在圆弧样条拟合中的应用[J].计算机辅助设计与图形学学报，2002，14（3）：222-224.

[9]涂嘉文，徐守时，谭勇.基于最小均方误差的圆弧分段曲线拟合方法[J].计算机应用，2001，21（3）：48-50.

[10]陈敏，姜小敏，陶涛，等.数控加工中平面参数曲线的拟合[J].机床与液压，2006，23（4）：70-72.

[11]蔡慧林，戴建强.基于遗传算法的相切圆弧逼近非圆曲线算法[J].兰州交通大学学报，2007，26（6）：5-8.

[12]郭文兰，张彤.曲线方程的双圆弧拟合算法及实现[J].哈尔滨理工大学学报，2004，9（6）：87-89.

[13]刘岩，马军.轧辊环状孔型曲面的建模与数控加工[J].太原重型机械学院学报，2003，24（3）：187-190,194.

[14]乐英，韩庆瑶，王璋奇.数控加工中非圆曲线的最小二乘圆弧逼近[J].华北电力大学学报，2006，33（6）：102-104.

[15]姚必强，姚进.数控加工曲线的等弧长圆弧拟合方法[J].四川大学学报:工程科学版，2008，40（1）：171-174.